Контрольная работа
Дисциплина: Высшая математика
Тема: Пределы. Сравнение бесконечно малых величин
Содержание
1. Предел числовой последовательности
2. Предел функции
3. Второй замечательный предел
4. Сравнение бесконечно малых величин
Литература
Предел числовой последовательности
Решение многих математических и прикладных задач приводит к последовательности чисел, заданных определенным образом. Выясним некоторые их свойства.
Определение 1.1. Если каждому натуральному числу 
по какому-то закону поставлено в соответствие вещественное число 
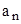, то множество чисел 
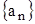называется числовой последовательностью.
Исходя из определения 1, видно, что числовая последовательность всегда содержит бесконечное число элементов. Изучение различных числовых последовательностей показывает, что с ростом номера их члены ведут себя по-разному. Они могут неограниченно увеличиваться или уменьшаться, могут постоянно приближаться к какому-то числу или вообще не проявлять какой-либо закономерности.
Определение 1.2. Число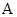 
называется пределом числовой последовательности 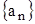, если для любого числа 
существует такой номер числовой последовательности 
, зависящий от 
, что для всех номеров числовой последовательности 
выполняется условие 
.
Последовательность, которая имеет предел, называется сходящейся. В этом случае пишут 
.
Очевидно, для выяснения вопроса о сходимости числовой последовательности необходимо иметь критерий, который был бы основан только на свойствах ее элементов.
Теорема 1.1. (теорема Коши о сходимости числовой последовательности). Для того, чтобы числовая последовательность была сходящейся, необходимо и достаточно, чтобы для любого числа существовал такой номер числовой последовательности , зависящий от , что для любых двух номеров числовой последовательности 
и 
, которые удовлетворяют условию и 
, было бы справедливо неравенство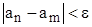 
.
Доказательство. Необходимость. Дано, что числовая последовательность 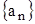сходится, значит, в соответствии с определением 2, у нее существует предел . Выберем какое-то число . Тогда, по определению предела числовой последовательности, существует такой ее номер , что для всех номеров выполняется неравенство . Но так как произвольно, то будет выполняться и 
. Возьмем два каких-то номера последовательности и , тогда
.
Отсюда следует, что 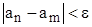, то есть необходимость доказана.
Достаточность. Дано, что 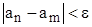. Значит, существует такой номер , что для данного условия и . В частности, если , а 
, то 
или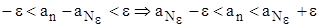 
при условии, что . Это значит, что числовая последовательность 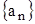для 
ограничена. Следовательно, по крайней мере, одна из ее подпоследовательностей 
должна сходиться. Пусть 
. Докажем, что 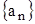сходится к 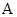также.
Возьмем произвольное . Тогда, согласно определению предела, существует такой номер 
, что для всех 
выполняется неравенство 
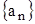. С другой стороны, по условию дано, что у последовательности существует такой номер , что для всех и будет выполняться условие 
.
Выберем 
и зафиксируем некоторое 
. Тогда для всех получим:
.
Отсюда следует, что , что и требовалось доказать.
Определение 1.3. Числовая последовательность 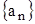называется монотонно возрастающей, если выполняется неравенство 
, и монотонно убывающей, если 
.
Теорема 1.2. Любая монотонно возрастающая ограниченная сверху числовая последовательность 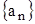имеет предел.
Аналогичная теорема есть и для монотонно убывающей числовой последовательности.
Предел функции
При исследовании графиков различных функций можно видеть, что при неограниченном стремлении аргумента функции к какой-то величине, то ли конечной, то ли бесконечной, сама функция также может принимать ряд значений, неограниченно приближающихся к некоторой величине. Следовательно, для функции также можно ввести понятие предела.
Определение 2.1. Число 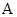называется пределом функции 
в точке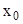 
, если для любого существует такое число 
, что из условия 
следует, что 
.
Данное условие записывается в виде: 
. Отметим, что интервал длины 
, который содержит в себе точку 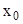, называется -окрестностью точки 
.
Аналогичным образом вводится понятие предела функции и при стремлении 
к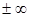 
. Так же как и в случае числовой последовательности, для функции существует теорема Коши, которая определяет существование у нее предела.
Теорема Коши о существовании предела. Для того чтобы функция , где 
, имела предел 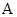при 
, где 
, необходимо и достаточно, чтобы для любого существовало такое число , что из условия 
вытекало условие 
.
Доказательства теоремы приводить не будем. В качестве предела функции могут служить как конечные, так и бесконечные величины.
Геометрический смысл теоремы Коши заключается в следующем. Возьмем некоторое , для которого 
. Тогда, согласно теореме, 
. Представим данное неравенство следующим образом: 
. Иначе говоря, как только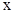 
станет отличаться от 
меньше, чем на 
, сама функция окажется в полосе шириной 
, расположенной на линии 
.
|
|
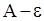
В приведенном определении предела и теореме Коши 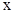может стремиться к 
произвольным образом. Однако во многих случаях это стремление происходит с какой-то одной стороны. Для этого вводятся понятия односторонних пределов.
Определение 2.2. Если 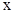стремится к , оставаясь все время меньше его, и при этом 
стремится к 
, то это число называется пределом функции слева и обозначается 
.
Определение 2.3. Если 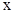стремится к , оставаясь все время больше его, и при этом стремится к , то это число называется пределом функции справа и обозначается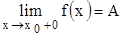 
.
Необходимо иметь в виду, что не всегда пределы слева и справа в точке равны между собой.