При координатных измерениях параметров поверхностей, которые представлены в конструкции деталей малыми сегментами, характерно то, что небольшие погрешности в исходных данных приводят к большим погрешностям в результатах измерений. Такая ситуация имеет место, например, при измерении прямолинейных профилей длиной до 2 мм. В программном обеспечении КИМ и других средств координатных измерений для определения параметров присоединенных элементов обычно используется метод наименьших квадратов, для чего минимизируется функция:
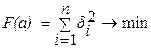
| (1) |
где a = a0, a1, … ai, … ak – искомые параметры присоединенного элемента;
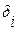– отклонения измеренных n точек от математического объекта.
В решении задачи (1) явно или неявно задействованы матрицы, вычисляемые по координатам X,Y,Z измеренных на поверхности точек. Если область измерения поверхности становится малой, то ухудшается обусловленность матрицы, а это ведет к тому, что малые изменения во входных данных влекут за собой большие изменения в результатах решения задачи. Данный класс задач принято называть плохо обусловленными. Поверхность решения такой задачи представляет «овраг» с почти горизонтальным дном, у которого нет четко выраженной точки минимума. Поэтому, в зависимости от начального приближения решение задачи (1) может оказаться в любой точке на дне получившегося «оврага».
Одним из путей решения проблемы плохой обусловленности может быть использование метода регуляризации, автором которого является академик А.Н.Тихонов. Суть метода состоит в добавлении к условию задачи некой дополнительной (априорной) информации, приводящей задачу к хорошо обусловленной. В этом случае, выражение (1) преобразуется в:
|
|
| (2) |
где 
- регуляризирующий член, содержащий сумму квадратов отклонений параметров от их номинальных значений:
 .
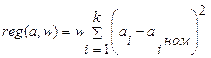| (3) |
Благодаря вводу в задачу регуляризирующего звена поверхность решения задачи имеет четкую точку минимума, что позволяет получить однозначное решение задачи.
Коэффициент регуляризации w является важным параметром в выражении (3). Если значение коэффициента w мало, то влияние номинальных значений параметров на конечное решение будет не достаточно для того, чтобы получить четкую точку минимума функции и решение будет зависеть в основном от суммы квадратов отклонений точек от поверхности, а значит, задача останется плохо обусловленной. При слишком большом коэффициенте - сумма квадратов отклонений точек от поверхности не будет оказывать нужного влияния на функцию минимизации, и решение будет подбираться максимально приближенным к номинальным значениям, практически без учета отклонений формы. Таким образом, выбор оптимального значения коэффициента регуляризации является важной задачей.
Одним из методов определения оптимального коэффициента регуляризации является метод L-кривой. Метод состоит в следующем: коэффициент регуляризации w изменяется от w min = 0 до w max с некоторым шагом. Для каждого значения коэффициента w рассчитываются параметры объекта, и строится график зависимостей, по вертикальной оси которого отложена сумма квадратов отклонений параметров от их номинальных значений, а по горизонтальной оси - коэффициент w. В начале кривой с ростом коэффициента w сумма квадратов отклонений параметров от их номинальных значений быстро уменьшается при незначительном увеличении w. При переходе через некоторую точку процесс изменяется, и уже небольшому уменьшению суммы квадратов отклонений параметров будет соответствовать существенное увеличение w. Характерная форма кривой дает возможность определить точку с максимальной кривизной, которая и будет соответствовать оптимальному коэффициенту регуляризации.
|
|
1. Смоделировать прямолинейный профиль (см. работу № 2) по уравнению 
, длина 0,1 мм. Для простоты моделирования принять, что прямая соответствует линии горизонта, поэтому коэффициенты kном = 0 и bном = 0. Число N точек измерения, равномерно расположенных по длине профиля, 3. Имитация погрешностей измерения координат точек осуществляется генерацией случайных чисел по нормальному закону распределения с математическим ожиданием равным 0 мм и средним квадратическим отклонением равным 0,002 мм. Измеренные значения координат (xi,yi) N точек получаются как сумма расчетных значений координат и случайных чисел.
2. Параметры присоединенной прямой определяются в соответствии с (2) и (3), поэтому минимизируется функционал:
|
Для определения оптимального значения коэффициент регуляризации w при нахождении параметров прямых значения w меняются от 0 до 0,03 с шагом 0,001.
3. Построить график зависимости, по вертикальной оси которой откладывается 
, а по горизонтальной оси - w. По графику определить оптимальный w и для этого значения параметры k и b (рис. 4).
4. Повторить пункты 1 – 3 для N равных 4 и 5. Сравнить результаты.
|
|
Рис. 4. Вид экрана Microsoft Excel (пункт 4)
Контрольные вопросы
1. Какие показатели исследуются при аттестации алгоритмов вычислений?
2. Что понимают под МХ программ вычислений?
3. Назовите причины погрешностей программ вычислений.
4. В каких случаях происходят изменения в программе вычислений?
5. Перечислите МХ программ вычислений.
6. Назовите методы определения погрешности программ вычислений.
7. Охарактеризуйте метод «образцовой меры» при оценке метрологических характеристик программ вычислений.
8. Охарактеризуйте метод «образцового прибора» при оценке метрологических характеристик программ вычислений.