Площадь поперечного сечения струйки и скорость движения идеального газа. Число М

Выясним, как изменяется скорость вдоль струйки газа при изменении площади поперечного сечения струйки. По уравнению расхода для струйки сжимаемой жидкости мы имеем

вдоль струйки. Дифференцируя это уравнение и деля затем почленно на rs 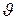получим

откуда

(5.7)

Воспользуемся теперь уравнением энергии в дифференциальной форме. Предположим, что силы трения в газе отсутствуют (жидкость идеальная) и движение газа горизонтальное (dz=0); тогда это уравнение примет вид:

или

Согласно первому закону термодинамики имеем

где V есть объем одного килограмма массы газа, равный 1/плотность. Принимая во внимание этот закон, получим из предыдущего равенства

(5.8)

Это равенство, которое наряду с уравнением расхода является основным для струйки газа, показывает, что в идеальной среде при установившемся течении возрастание скорости вдоль струйки всегда сопровождается уменьшением давления и, наоборот, уменьшение скорости – возрастанием давления.

Формула (5.7) теперь может быть записана в виде

или в виде

(5.9)

Рис. 5.3. Изменение скорости вдоль стенки канала а) – в дозвуковом, б) – в сверхзвуковом потоке

Последнее равенство устанавливает зависимость между площадью поперечного сечения струйки и скоростью движения газа.

Из уравнения (5.9) видно, что характер зависимости скорости от площади поперечного сечения струйки оказывается различным. Смотря по тому, происходит ли движение газа с дозвуковой или сверхзвуковой скоростью.

Если q > а то выражение в скобках отрицательное по знаку и, следовательно, знак ds обратен знаку dq. Это означает, что если вдоль струйки площадь поперечного сечения возрастает, то скорость в ней убывает, и наоборот, если площадь поперечного сечения убывает, то скорость возрастает.

Иными словами,

Если q > а то соотношения между площадью поперечного сечения струйки и скоростью будет количественно иным, нежели в случае несжимаемой жидкости. При q > а выражение в скобках положительно по знаку. И, следовательно, знак ds совпадает со знаком dq. Это означает, что если вдоль струйки площадь поперечного сечения возрастает, то и скорость при этом возрастет и, наоборот, сжатие струйки сопровождается уменьшением скорости (рис. 5.3).

Отношение скорости движения газа к скорости распространения звука мы будем называть числом M.

В дозвуковой области М<1, в сверхзвуковой М>1; в несжимаемой среде М=0 при любой скорости движения. Введя число М, можно записать уравнение (5.9) в виде

(5.10)

Для того чтобы выяснить механический смысл числа М, обратимся к формуле (5.7). Сопоставляя ее с последним равенством, видим, что

Знаменатель этого выражения dq/q представляет собой относительное изменение скорости. Числитель dr/r представляет собой относительное изменение плотности среды при изменении ее скорости. Таким образом,

Иными словами, число М, так же как и скорость звука, является характеристикой сжимаемости среды; но скорость звука как характеристика сжимаемости относится к покоящейся среде, тогда как число М связано с движущейся средой; оно является характеристикой сжимаемости потока газа.

Число М имеет поэтому фундаментальное значение во всей теории движения газов.

Из последнего соотношения следуют и другие важные выводы. Это соотношение показывает, что знак dr при установившемся течении всегда противоположен знаку dq, т.е. при нарастании скорости вдоль струйки плотность газа уменьшается, и наоборот. Далее, из этого соотношения видно, что при дозвуковом течении газа относительное изменение плотности меньше относительного изменения скорости, тогда как при сверхзвуковом течении относительное изменение плотности превосходит относительное изменение скорости.

Уравнение (5.10) позволяет объяснить действие так называемого сопла Лаваля, которое позволяет получить больших скоростей течения газа. Сопло Лаваля представляет собой насадок, состоящий из короткой сужающейся части и следующей за нею более длинной расширяющейся частью (рис. 5.4). Если поток газа, протекающий сквозь сопло Лаваля, имеет везде скорость, меньшую скорости распространения звука. То изменение скорости происходит по кривой типа а на рис. 5.4; во входной части скорость нарастает, в сжатом сечении достигает максимума и в выходной части убывает.е.сли поток газа имеет везде сверхзвуковую скорость, то изменение скорости вдоль сопла происходит по кривой типа б: во входной части скорость уменьшается, в сжатом сечении достигает минимума и затем в выходной части нарастает.е.сли сопло спроектировано так, что в сжатом сечении q=a, то обе кривые соприкоснуться в точке, соответствующей этому сечению (пунктирные кривые на рис. 5.4). При этом по инерции поток продолжает ускоряться в сечении, где q=a и распределение скорости переходит с кривой типа а на кривую типа б, т.е. в этом случае сопло Лаваля плавно переводит дозвуковой поток в сверхзвуковой.

Рис. 5.4. Скорость газа в сопле Лаваля при дозвуковом и сверхзвуковом течении газа

Сопло Лаваля применяется в сверхзвуковых аэродинамических трубах, паровых и газовых турбинах, турбореактивных двигателях и т.д. Впервые оно было применено в 1889 г. Шведским инженером Лавалем в конструкции быстроходной паровой турбины. Желая получить возможно большую кинетическую энергию струи пара, удар которой о рабочие лопатки приводит во вращение рабочее колесо турбины, Лаваль применял сначала сужающиеся насадки. Однако опыт показал, что как только в выходном сечении такого насадка достигается скорость истечения, равная скорости звука, дальнейшее нарастание скорости при сужении насадка прекращается. Тогда Лаваль присоединил к сужающемуся насадку, в котором была достигнута звуковая скорость, расширяющийся насадок, и оказалось, что при таком расширении скорость потока продолжает нарастать, и поток из дозвукового переходит в сверхзвуковой.