Особенности сверхзвуковых течений газа

Рис. 5.1. Свойства несжимаемой жидкости
Прежде чем интегрировать уравнение энергии для сжимаемой жидкости, рассмотрим некоторые ее особенности. Представим себе сначала несжимаемую жидкость, находящуюся в длинной трубке и ограниченную поршнями А и В (рис. 5.1). В силу несжимаемости жидкости всякое перемещение поршня А вызовет в тот же момент такое же перемещение поршня В (так, как если бы между А и В было твердое тело). Иными словами, изменение давления, вызванные перемещениями поршня А, передаются в несжимаемой жидкости мгновенно, т.е. с бесконечно большой скоростью. Иначе обстоит дело в сжимаемой жидкости. При перемещении поршня перед ним возникает уплотнение, которое передвигается вперед с конечной скоростью, зависящей от состояния и свойств жидкости. Вычислим скорость распространения в газе малых (упругих) возмущений.
Пусть за время dt поршень продвинулся на длину ds, а вызванное им возмущение распространилось вдоль трубы на длину dx. Рассматривая газ как упругую среду и применяя к нему известный закон пропорциональности между изменением давления и относительной деформацией, можно записать, что сила приходящаяся на единицу площади поперечного сечения трубы, равна произведению модуля упругости для газа на относительное удлинение. Так как в движение приведена часть газа длиною (вдоль трубы) dx, а в результате перемещения поршня эта длина уменьшилась на ds, то будем считать за относительное удлинение величину ds/dx; тогда получим:


где F есть приложенная поршнем сила, Е - модуль Юнга для газа, а S - площадь поперечного сечения трубы.
Применим к массе газа, приведенной поршнем в движение, теорему импульсов, которая, как известно из курса общей механики, формулируется следующим образом: дифференциал количества движения материальной системы равен элементарному импульсу действующих на систему внешних сил: Fdt=d(mV). В данном случае масса газа, приведенная в движение, равна rSdx, и если предположить ввиду малости dx, что все частицы этой массы движутся с одной и той же скоростью, равной ds/dt, то полученное массой количество движения будет равно

Следовательно, по теореме импульсов

| (5.1) |
Здесь dx/dt представляет собой интересующую нас скорость распространения упругих возмущений; обозначив ее через а, получим

откуда

| (5.2) |
Такая же формула получилась бы в том случае, если бы газ не был ограничен стенками трубы, а вместо поршня был другой источник возмущения (изменения давления), как, например, звучащий камертон. В этом последнем случае формула (5.2) давала бы величину скорости распространения звуковых колебаний в газе, которые. Как известно из физики, представляют собою продольные упругие колебания.
Рассмотрим более общий случай, когда продольные упругие колебания исходят из какой-либо точки, распространяются в неограниченной газовой среде. Вычислим и для этого случая скорость распространения этих колебаний. Вследствие симметрии, колебания давления будут распространяться с одинаковой для всех направлений скоростью а по прямым линиям, проходящим через начальную точку. Через t секунд после начала распространения колебаний они достигнут поверхности сферы с центром в начальной точке и радиусом, равным at (рис. 5.2.). За время dt радиус этой сферы увеличится еще на dr=a dt. Объем V массы газа, на которую распространилось возмущение за время dt, приближенно можно считать равным


Рис. 5.2. Скорость продольных, упругих колебаний в газе от точечного источника
Если обозначить через v скорость движения газа, вызванную прохождением волны давления или разрежения сквозь поверхность сферы радиусом r, то изменение объема V за время dt запишется в виде

Отсюда следует, что относительная объемная деформация равна

По закону пропорциональности между изменением давления и относительной объемной деформацией можем написать

| (5.3) |
где Е есть модуль упругости в данной точке газовой среды. Следовательно, в данном случае


Выделим теперь из массы газа, находящейся между сферами с радиусами r и r+dr, часть, ограниченную боковой поверхностью конуса с вершиной в источнике возмущения и телесным углом, равным dW. Применим к этой части теорему импульсов. Так как выделенная масса равна

то, предполагая, как и в предыдущем выводе, скорость всех частиц в объеме dV одинаковыми, получим, что количество движения равно

Импульс сил давления равен

По теореме импульсов находим:

Сравним это выражение для dp с предыдущим, вновь получаем формулу (5.2).
Величину модуля Юнга для газа можно выразить через давление и плотность. В самом деле, для малого объема газа V уравнение неразрывности движения можно приближенно записать в виде

отсюда
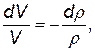
по формуле (5.3) находим

Подставляя это выражение в формулу (5.3), получим:

| (5.4) |
Из этой формулы видно, что
| скорость распространения звука является одной из важнейших механических характеристик газа, именно характеристикой его сжимаемости. |
Действительно, величина dr/dр представляет собой изменение плотности, приходящееся на единицу изменения давления и непосредственно связана с коэффициентом сжимаемости bр.

Отсюда следует, что

т.е. что
| а также является характеристикой сжимаемости среды: чем более сжимаема среда, тем меньше скорость распространения звука и наоборот. |
Для несжимаемой среды а=µ. Процесс распространения упругих колебаний давления в газе можно рассматривать, как адиабатический процесс, так как он протекает достаточно быстро для того, чтобы обмен теплотой у частиц газа не успевал происходить. Влиянием вязкости при этом можно пренебрегать. Для адиабатического процесса зависимость давления от плотности определяется уравнением адиабаты

где k есть показатель адиабаты, а р0 и r0 суть давления и плотности в некоторой фиксированной точке. Следовательно,

| (5.5) |
и для а получаем формулу

| (5.6) |
Так как по уравнению состояния газа р/r=RT где R есть газовая постоянная, а Т – абсолютная температура, то можно также написать, что

Из кинетической теории газа известно, что средняя скорость теплового движения молекул газа также пропорциональна T1/2 . Отсюда следует, что чем быстрее движутся молекулы газа, тем с большей скоростью происходит в нем передача малых колебаний давления.
| Таким образом, в газах, в отличие от несжимаемой жидкости, упругие возмущения распространяются с конечной скоростью а, разной в разных точках и зависящей для данного газа только от отношения давления к плотности в данной точке (5.6) или от абсолютной температуры в данной точке (5.6'). |
Величина скорости звука а, которая, как уже указывалось, является характеристикой сжимаемости газа, играет важнейшую роль во всей механике газа; как увидим в дальнейшем, законы движения газа резко отличаются друг от друга в зависимости от того, больше ли скорость движения газа скорости распространения звука или меньше ее. Рассмотрим простейшие примеры этого различия в следующем параграфе.