Если в потоке газа находится препятствие, то, как известно из предыдущего, на передней стороне препятствия всегда расположена точка В, в которой скорость равна нулю; эта точка называется точкой торможения потока (рис. 5.4).
Исследования течения газа показали, что в точке торможения потока давление, плотность и температура газа достигают максимальных значений, возможных в данном потоке. Их необходимо знать, в частности, для измерения скорости потока газа с помощью скоростной трубки и его температуры с помощью термометра. Вычислим эти максимальное значения, предполагая, что торможение потока при приближении к препятствию происходит адиабатический и с постоянной энтальпией.
Возьмем в струйке, проходящей через точку торможения А два поперечных сечения: одно – далеко перед препятствием (на бесконечности), где скорость движения газа равна Vі, другое, где скорость равна нулю. Будем отмечать величины, относящиеся к первому сечению, индексом і, а величины, относящиеся ко второму сечению, - индексом 0. Уравнение энергии, написанное для этих двух сечений, будет иметь вид

Рис. 5.5. Схема торможения потока газа

Отсюда, деля почленно на

получаем
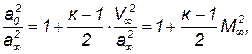
| (5.11) |
где Mі=Vі/aі. Подставим сюда вместо а его выражение через температуру Т, тогда получим следующую формулу для температуры в точке адиабатического торможения потока газа аналогичную выражению (3.49) выведенному выше для общего случая движения газа:

| (5.12) |
Из этой формулы видно, что в точке торможения потока газа температура больше, чем в набегающем потоке; при этом превышении Т0 над температурой окружающей среды Tµ пропорционально квадрату числа М набегающего потока газа:
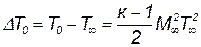
Зависимость температуры торможения адиабатического потока газа от числа М набегающего потока и температуры окружающей среды представлена в виде графика на рис. 5.6.
При значениях числа М, которые имеют место в современной авиационной и ракетной технике, температура торможения может достигать очень больших величин. Так, например, если ракета летит на высоте 20 км со скоростью 5350 км/час (М =5), то при температуре окружающей среды, равной (по МСА) Тµ=216ºК(-57ºС), температура торможения по формуле (5.12) будет равна

и, следовательно, DТ=1080° Температура торможения, полученная в этом примере, превосходит температуру плавления стали (уже при М=3 температура торможения на уровне моря (Т0=806К) превосходит температуру плавления алюминия). Поэтому носок корпуса ракеты, если он выполнен из перечисленных металлов и не приняты меры к его охлаждению, в полете будет оплавляться. Действительная температура воздуха не только у носка, но и на всей остальной поверхности летящего тела близка к температуре торможения (вычисленной по местной скорости обтекания и местной скорости звука); она несколько меньше этой температуры вследствие того, что часть энергии затрачивается на работу сил трения воздуха.

Рис. 5.6. Термодинамические параметры изоэнтропического потока газ
| Превышение температуры воздуха у поверхности летящего тела температурой окружающей среды носит название аэродинамического нагрева поверхности. |
Это представляет собой одну из серьезнейших и труднейших проблем современной авиационной и ракетной техники. Серьезность этой проблемы состоит в том, что при существующих материалах и способах охлаждения поверхности аэродинамический нагрев ставит преграду дальнейшему росту скорости полета (тепловой барьер). Трудность состоит не только в отборе и отводе значительного количества тепла с поверхности летящего тела, но и в том, что с возрастанием скорости температура воздуха у поверхности быстро возрастает.
Вычислим давление и плотность газа в точке адиабатического торможения, тогда получим:

Из уравнения адиабатического процесса следует:

подставляя это выражение в предыдущее равенство и решая его относительно р0/рµ находим:
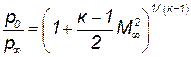
| (5.13) |
Отсюда по уравнению адиабатического процесса получаем выражение для плотности
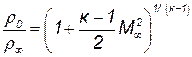
| (5.14) |
Зависимости (5.13) и (5.14) представлены в виде графиков на рис. 5.6. Следует отметить, что в формуле (5.13) можно полгать M µ=0 лишь в том случае, когда qі=0 при aі=0 т.е. для случая несжимаемости жидкости, эта формула непосредственно непригодна, так как при ее выводе использована зависимость скорости звука от давления, относящаяся только к газу.
Волны Маха
Интенсивность косого скачка изменяется с изменением угла наклона его фронта к направлению набегающего потока. В предельном случае, когда косой скачок переходит в прямой (а=90), увеличение давления получается максимальным.
Другой предельный случай наблюдается тогда, когда сверхзвуковой поток обтекает бесконечно тонкую струну, расположенную перпендикулярно вектору скорости набегающего потока, или сферу бесконечно малых размеров. В этом случае в потоке возникают бесконечно малые возмущения давления, которые будут распространяться во все стороны со скоростью звука a.

Рис. 5.7. Схема образования слабых волн возмущений
Допустим, что в некоторой точке О сверхзвукового потока находится тело бесконечно малых размеров (сфера или струна). Тогда слабая волна сжатия станет распространяться во все стороны из центра возмущения О со скоростью звука а. Через единицу времени t, допустим, через одну секунду, фронт волны будет представлять собой сферу радиуса r=а или цилиндр того же радиуса. Однако вся масса газа, в которой возникла волна, сносится по потоку со сверхзвуковой скоростью wH>а. По этой причине слабые волны давления никогда не выйдут за пределы конуса или клина, поверхность которых является огибающей для сферических или цилиндрических волн Образующая такого конуса носит название волны или характеристики Маха. Угол aо между образующей и осью называется углом Маха или углом распространения слабых возмущений. Этот угол, как видно из схемы образования слабых волн возмущений, определяется равенством.

| (5.15) |
Сильные волны возмущения, как было показано выше, распространяются со сверхзвуковой скоростью, в связи с чем фронт сильного скачка образует с набегающим потоком угол, больший, чем характеристика: a>aо.
Таким образом, диапазон изменения угла a для косого скачка уплотнения определяется следующими пределами aо£a£90º.