Рассмотрим истечение газа из сосуда, внутри которого все параметры газа заторможенные, т.к. w=0. В соответствии с (3.23)

или

Нетрудно убедиться, что максимальная скорость газа на срезе сопла будет в том случае, кода энтальпия газа в движущемся потоке станет равной нулю (рис. 3.6).
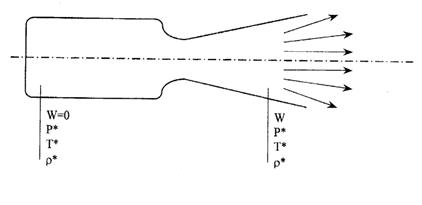
Рис. 3.6. Схема течения газа в сопле
Это может быть в том случае, когда температура газа в потоке снизится до нуля, т.е. когда вся энтальпия газа полностью преобразуется в кинетическую энергию
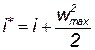
Отсюда можно найти значение максимальной скорости газа

| (3.29) |
Для воздуха в предположении, что СP=соnst, формула (3.29) дает
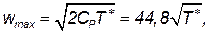
где СP=1005 Дж/кг К.
Если температура торможения воздуха в сосуде близка к нормальной (Т*≈300К), то максимально возможная скорость истечения wmaх=776 м/с.
Увеличение максимальной скорости истечения может быть достигнуто только за счет увеличения температуры торможения. Обратим внимание на то, что давление в баллоне в этом случае не влияет на максимальную скорость истечения. Объяснение этому явлению будет дано ниже.
Чтобы перевести газ из состояния покоя в движение, нужно израсходовать часть энтальпии:

или

Разделим правую и левую часть последнего уравнения на температуру газа в потоке

Умножим числитель и знаменатель правой части на kR
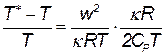
| (3.30) |
Преобразуем выражение KR/2CP, для чего используем известные соотношения термодинамики: CP-C V =R и CP/C V =K

Учитывая, что скорость звука

выражение (3.30) приведем к виду

Так как число Маха равно w/а, получим

И окончательно

| (3.31) |
Отсюда следует, что максимальное значение числа М (при T=0) равно бесконечности. Этот факт объясняется тем, что при достижении максимальной скорости вместе с абсолютной температурой обращается в ноль и скорость звука.
Поскольку скорость движения газа может быть как выше, так и ниже скорости звука, существует режим, при котором скорость потока равна скорости звука. В этом случае М=1 этот режим называется критическим всем параметрам газа при этом режиме присваивается нижний индекс " кр."
Из (3.31) можно получить выражение для критической температуры (М=1)
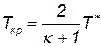
| (3.32) |
Из (3.32) следует, что для того чтобы газ разогнать до скорости звука, его температура должна понизиться в (2/к+1) раз. Для воздуха к=1,4 и (2/к+1) =0,833. Если температура торможения газа в баллоне Т*=1000К, то когда он разгонится до скорости звука, его температура станет 833К.
Скорость звука с (3.32) при критическом режиме течения равна

| (3.33) |
где а * -скорость звука в покоящемся газе.
Запишем снова уравнение энергии в виде

| (3.34) |
Разделим правую и левую часть (3.34) назначение энтальпии при критическом режиме:
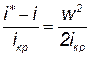
или

| (3.35) |
Далее, используя соотношения CP-Cn=R и CP/Cn=к, выразим в левой части (3.35) Ткр через Т* в соответствии с (3.32). Тогда получим:
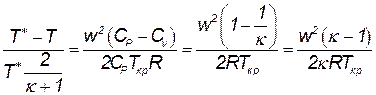
или

| (3.36) |
Помимо числа M=w/a в авиационной технике используется так называемая приведенная скорость l, которая равна отношению скорости потока к критической скорости звука
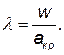
Используя это соотношение, уравнение (3.36) можно привести к виду
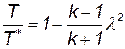
| (3.37) |
На критическом режиме lкр=Мкр=1. Максимальной скорости потока соответствует максимальное значение приведенной скорости

Для воздуха к=1,4; lmax=2,45.
Связь между М и l описывается соотношениями:
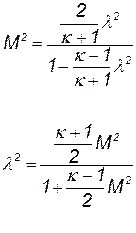
| (3.38) |
В газовой динамике, теории лопаточных машин и реактивных двигателей используется оба безразмерных критерия М и l В одних случаях более простые соотношения получаются при использовании приведенной скорости, в других - числа М.