Уравнение энергии (3.18) содержит тепловые величины (qнар, i2, i1) и не содержит давления и плотности газа. Можно получить иную механическую форму уравнения, куда, наоборот, не входит температура газа и тепло, а скорость движения связана с давлением и плотностью. Для этого воспользуемся формой записи первого закона термодинамики в виде

| (3.39) |
После интегрирования с учетом того, что v=1/r имеем

| (3.40) |
Уравнение первого закона термодинамики записано для покоящейся жидкости или, что то же самое, для жидкости, движущейся вместе с системой координат. Учитывая это, вычтем из (3.18) уравнение (3.13), помня, что q=qнар+qT в результате получим

Это мы вправе делать, несмотря на то, что уравнение (3.23) записано для движущейся жидкости, так как значение температуры газа Т, количества тепла q, давления Р и плотности r не зависят оттого, в какой системе координат они измеряются.
Так как тепло трения равно работе, затрачиваемой на преодоление сил трения (qТР=lТР), то уравнению энергии можно придать следующий вид

| (3.41) |
Это уравнение, называемое уравнением Бернулли, имеет четкий физический смысл. Техническая работа, совершаемая газом (рис. 3.4, а)

расходуется на полезную работу расширения (например, в колесе турбины), на увеличение кинетической энергии газов

и на преодоление сил трения lТР
Посредством (3.41) можно вычислить, например, работу, которую отдает газ колесу турбины, стоящему между сечениями 1 и 2, если все остальные члены уравнения известны. Если величина / получится отрицательной, то это значит, что между сечениями 1 и 2 стоит компрессор и работа к газу подводится. Для того чтобы пользоваться уравнением Бернулли для сжимаемого газа, необходимо знать термодинамический процесс изменения состояния газа, так как без этого неизвестна зависимость плотности газа от давления, и нельзя вычислить интеграл (рис. 3.4, а).

Вычислим этот интеграл для основных термодинамических процессов. Для изохорического процесса p=const
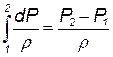
| (3.42) |
Это соотношение используется в гидравлике, например, для определения мощности насоса или турбины.
При изобарическом процессе Р=const

| (3.43) |
Для изотермического процесса P/r=RT=const.
Из уравнения состояния
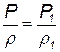
имеем

Это позволяет взять интеграл
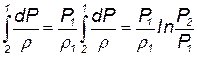
| (3.44) |
Если состояние газа изменяется по идеальной адиабате

тогда

и
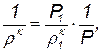
откуда

Интегрирование дает

| (3.45) |
Для политропического процесса с постоянным показателем политропны P/rn=const

| (3.46) |
Важно отметить, что подводимое к газу тепло непосредственно не отражено в уравнении Бернулли. Однако оно учитывается при вычислении интеграла, т.к. влияет на вид функции р=f(Р), т.е. на характер процесса, по которому изменяется состояние газа.
Наибольшее значение в газовой динамике и теории реактивных двигателей имеет идеальный адиабатический процесс, который предполагает отсутствие теплообмена с окружающей средой и работы сил трения. Энтропия в таком процессе не изменяется. Если нет технической работы, и процесс идеальный адиабатический, то уравнение Бернулли (3.41) примет следующий вид

| (3.47) |
т.е. совершаемая газом техническая работа (рис. 3.4, а) целиком тратится на увеличение кинетической энергии газа.
Если поток газа при скорости, соответствующей числу М, затормозить полностью, то в соответствии с (3.31) его температура возрастет от значения T до T*

Если процесс торможения идет по идеальной адиабате, то, воспользовавшись уравнениями

и
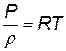
0можно связать отношение температуры T*/T с отношением давлений

| (3.48) |
Подставив (3.48) в (3.31) получим

| (3.49) |
Аналогично свяжем отношение температуры T*/T с отношением r*/r

| (3.50) |
тогда получим

| (3.51) |
С помощью уравнения (3.37), связывающего отношение температур T*/T с приведенной скоростью, используя (3.39) и (3.40), можно получить

| (3.52) |

| (3.53) |
Истинное давление, которое получается при торможении струи газа, может существенно отличаться от полного давления, определенного из выражений (3.49) и (3.52).
Объясняется это тем, что в действительности торможение осуществляется не по идеальной адиабате, а с гидравлическими потерями, что, естественно, приводит к выделению тепла трения в потоке. Если на участке струи 1 - 2 наблюдаются потери, то это обязательно приводит к тому, что полное давление в сечении 2 будет ниже полного давления в сечении 1: Р2*<Р1* Величина гидравлических потерь оценивается коэффициентом сохранения полного давления

| (3.54) |
Чем больше потери, тем ниже значение коэффициента сохранения полного давления и меньше полное давление в сечении 2

| (3.55) |
Коэффициент сохранения полного давления связан с изменением энтропии в потоке газа, и, следовательно, с количеством выделившегося тепла в результате работы сил трения. Для того чтобы убедиться в этом, перейдем в равенстве (3.20) от параметров потока к параметрам торможения, используя соотношение Рvк=P*v*к=const. Получим

| (3.56) |
Выразив удельный объем через давление и температуру, используя уравнения состояния

и подставив v * в (3.56), после ряда преобразований можно получить

| (3.57) |
Так как полное давление в газовом потоке вследствие потерь падает Р*2<Р*1, тепло трения имеет всегда положительный знак (dqтр>0) и соответственно энтропия возрастает (S2>S1,). Заменив в уравнении (3.57) отношение давлений через s, получим

| (3.58) |