Выбор варианта задания и требования к оформлению
1) Необходимо выбрать из таблиц 2.1 и 2.2, прилагаемых к условию задания, данные в соответствии со своим вариантом. Номер схемы нагружения совпадает с номером варианта.
2) Расчетно-проектировочная работа выполняется на бумаге формата А4.
3) Расчетно-проектировочная работа должна содержать условие задания, расчетно-графическую схему с указанием на ней в числах всех величин и решения с кратким объяснением. Расчеты выполняются в единицах системы СИ (для удобства допускается использование производных единиц).
Расчетно-проектировочная работа «Расчет на прочность и жесткость стержня при центральном растяжении и сжатии»
Дан стальной стержень (модуль упругости Е = 2·105 МПа), нагруженный сосредоточенными силами F1, F2, F3. Стержень состоит из трех участков, два из которых имеют одинаковый тип и размер поперечного сечения.
Требуется:
1 Построить эпюру продольной силы Nz по длине стержня.
2 Определить из расчета на прочность при σadmр = σadmс = 160 МПа размеры поперечных сечений стержня: прямоугольное поперечное сечение (h\b=2); круглое сплошное поперечное сечение. Выполнить проверку условия прочности. Построить эпюру нормальных напряжений σ по длине стержня и эпюры распределения нормальных напряжений σ по поперечным сечениям.
3 Определить изменение длины стержня под действием внешних сил и построить эпюру перемещений поперечных сечений. Выполнить проверку условия жесткости стержня, если Δ ladm = 1 мм.
Таблица 2.1 - Исходные данные
| № варианта | F1, kH | F2, kH | F3, kH | l 1, м | l 2, м | l 3, м |
| 0,1 | 0,2 | 0,1 | ||||
| 0,2 | 0,1 | 0,3 | ||||
| 0,2 | 0,1 | 0,2 | ||||
| 0,1 | 0,2 | 0,3 | ||||
| 0,2 | 0,1 | 0,1 | ||||
| 0,2 | 0,1 | 0,3 | ||||
| 0,1 | 0,2 | 0,2 | ||||
| 0,1 | 0,3 | 0,2 | ||||
| 0,3 | 0,2 | 0,3 | ||||
| 0,2 | 0,3 | 0,2 | ||||
| 0,2 | 0,1 | 0,2 | ||||
| 0,2 | 0,1 | 0,2 | ||||
| 0,2 | 0,3 | 0,2 | ||||
| 0,3 | 0,1 | 0,3 | ||||
| 0,1 | 0,3 | 0,1 | ||||
| 0,1 | 0,2 | 0,3 | ||||
| 0,1 | 0,2 | 0,1 | ||||
| 0,1 | 0,3 | 0,1 | ||||
| 0,2 | 0,3 | 0,2 | ||||
| 0,1 | 0,3 | 0,1 | ||||
| 0,2 | 0,3 | 0,1 | ||||
| 0,1 | 0,2 | 0,2 | ||||
| 0,2 | 0,1 | 0,2 | ||||
| 0,2 | 0,3 | 0,2 | ||||
| 0,3 | 0,2 | 0,3 | ||||
| 0,1 | 0,3 | 0,1 | ||||
| 0,3 | 0,2 | 0,3 | ||||
| 0,1 | 0,2 | 0,1 | ||||
| 0,1 | 0,3 | 0,2 | ||||
| 0,2 | 0,3 | 0,2 |
Таблица 2.2 - Схемы нагружения стержня
   №1 №1

|      №2 №2
| |||
  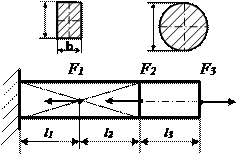 №3 №3
|     №4 №4
| |||
   №5 №5
|     №6 №6
| |||
     №7 №7
|      №8 №8
| |||
№9
|    №10 №10
|
Продолжение таблицы 2.2
  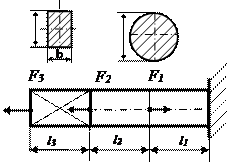 №11 №11
|  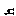   №12 №12
| |||||||||||
   №13 №13
|     №14 №14
| |||||||||||
    №15 №15
|    №16 №16
| |||||||||||
  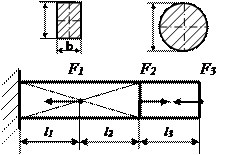 №17 №17
|    №18 №18
| |||||||||||
№19
|   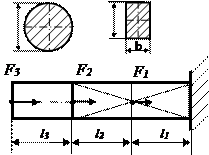 №20 №20
|
Продолжение таблицы 2.2
   №21 №21

|     №22 №22
| |||
   №23 №23
|     №24 №24
| |||
№25
  
|    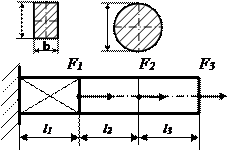 №26 №26
| |||
   №27 №27
|    №28 №28
| |||
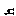   №29 №29
|     №30 №30
|
Пример выполнения расчетно-проектировочной работы
Дан стальной стержень (модуль упругости Е = 2·105 МПа), нагруженный сосредоточенными силами F1, F2, F3. Стержень состоит из трех участков, два из которых имеют одинаковый тип и размер поперечного сечения.
Требуется:
1 Построить эпюру продольной силы Nz по длине стержня.
2 Определить из расчета на прочность при σadmр = σadmс = 160 МПа размеры поперечных сечений стержня: прямоугольное поперечное сечение (h\b=2); круглое сплошное поперечное сечение. Выполнить проверку условия прочности. Построить эпюру нормальных напряжений σ по длине стержня и эпюры распределения нормальных напряжений σ по поперечным сечениям.
3 Определить изменение длины стержня под действием внешних сил и построить эпюру перемещений поперечных сечений. Выполнить проверку условия жесткости стержня, если Δ ladm = 1 мм.


Рисунок 3.1 – Схема ступенчатого стержня
Определим реакции опор.
Введем декартову систему координат. Ось z совместим с осью стержня; оси x и y расположим в плоскости поперечного сечения (рисунок 3.2, а). За положительное направление оси z выберем направление, указанное на чертеже.
Под действием внешней нагрузки в жестко защемленной опоре возникает реакция опоры НА (рисунок 3.2, а), которая определяется из уравнения равновесия статики. Линия действия реакции опоры НА совпадает с осью стержня и линиями действия внешних сил F1, F2 и F3. Направление реакции опоры НА выбираем произвольно (в данном случае совпадает с направлением оси z). Спроецируем все усилия (НА, F1, F2 и F3) на ось z:
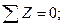
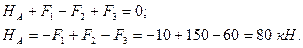
2 Определим продольную силу Nz на каждом участке нагружения стержня и построим эпюру.
Разбиваем данный ступенчатый стержень на участки. Границам участков являются места приложения внешних сил и изменения размеров поперечного сечения. Обозначим границы участков буквами А, В, С и D, начиная от жесткой заделки. Стержень состоит из трех участков нагружения: участок АВ, участок ВС и участок СD (рисунок 3.2, а). Причем, участки АВ и ВС имеют одинаковые тип и размеры поперечного сечения - прямоугольное сечение; участок СD – круглое сплошное сечение.
Для определения продольной силы Nz используем метод сечений: на каждом участке проведем сечение, перпендикулярное оси стержня; отбросим одну часть стержня; рассмотрим равновесие оставшейся части. Рассмотрим каждый участок в отдельности.
Участок АВ (0 ≤ z1 ≤ 0,1 м )
Проведем сечение I-I, перпендикулярное оси стержня, на расстоянии z1 от точки А. Отбросим правую от сечения часть стержня. Рассмотрим равновесие оставшейся левой части стержня. На левую часть стержня действует реакция опоры НА, которая направлена к проведенному сечению, следовательно, подставляем ее значение в формулу со знаком «-». Таким образом, в поперечном сечении I-I возникает продольная сила  :
:
 (уравнение константы).
(уравнение константы).
Продольная сила  в сечении I-I сжимающая, что означает сжатие участка АВ.
в сечении I-I сжимающая, что означает сжатие участка АВ.
Участок ВС, (0 ≤ z2 ≤ 0,2 м )
Проведем сечение II-II на расстоянии z2 от точки В. Отбросим правую от сечения часть стержня. Рассмотрим всю левую часть стержня. На левую часть стержня действуют силы HA и F1. Сила F1 и реакция опоры HA направлены к сечению, следовательно, подставляем их значения в формулу со знаком «-». Таким образом, в поперечном сечении II-II возникает продольная сила  :
:
 (уравнение константы).
(уравнение константы).
Продольная сила  в сечении II-II сжимающая, что означает сжатие участка ВС.
в сечении II-II сжимающая, что означает сжатие участка ВС.
Участок CD (0 ≤ z3 ≤ 0,3 м )
Проведем сечение III-III на расстоянии z3 от точки D. Отбросим правую от сечения часть стержня. Рассмотрим всю левую часть стержня. На левую часть стержня действуют силы HA, F1 и F2. Сила F1 и реакция опоры HA направлены к сечению, следовательно, подставляем их значения в формулу со знаком «-». Сила F2 направлена от сечения, следовательно, подставляем ее значение в формулу со знаком «+». Таким образом, в поперечном сечении III-III возникает продольная сила  :
:
 (уравнение константы).
(уравнение константы).
Продольная сила  в сечении III-III растягивающая, что означает растяжение участка CD.
в сечении III-III растягивающая, что означает растяжение участка CD.
По найденным значениям продольных сил для каждого участка строим эпюру продольных сил  (рисунок 3.2, б). Проверим правильность построения эпюры: в сечениях стержня, где приложены сосредоточенные нагрузки, на эпюре будут скачки, равные по величине приложенной сосредоточенной силе.
(рисунок 3.2, б). Проверим правильность построения эпюры: в сечениях стержня, где приложены сосредоточенные нагрузки, на эпюре будут скачки, равные по величине приложенной сосредоточенной силе.
3 Определим из расчета на прочность при σadmр = σadmс = 160 МПа размеры поперечных сечений стержня. Выполним проверку прочности по участкам. Построить эпюру нормальных напряжений σ по длине стержня и эпюры распределения нормальных напряжений σ по поперечным сечениям.
Для определения размеров поперечных сечений используем формулу проектного расчета для определения требуемой по условию прочности площади опасного поперечного сечения.
Определим сечения, в которых возникает максимальная продольная сила (опасные сечения), на каждом участке стержня. В пределах каждого участка продольная сила постоянна. Следовательно, на каждом участке все сечения равноопасны.
По условию задачи участки АВ и ВС имеют одинаковые тип и размеры поперечного сечения. На участке ВС продольная сила по абсолютному значению больше, чем на участке АВ. Поэтому расчет требуемой площади поперечного сечения будем вести по участку ВС.
Участок ВС (0 ≤ z2 ≤ 0,2 м )
Участок ВС по условию задачи имеет прямоугольное поперечное сечение со сторонами b и h, причем h\b=2.
Требуемая площадь поперечного сечения из условия прочности равна:

Площадь прямоугольника с учетом условия задачи определяется по формуле:
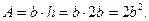
Откуда находим, что

Назначаем b = 1,7 см.
Из заданного соотношения сторон прямоугольного сечения (h\b=2), находим, что:



Определим нормальные напряжения при назначенных размерах поперечного сечения стержня на участке ВС, учитывая, что фактическая площадь поперечного сечения определяется по формуле 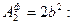
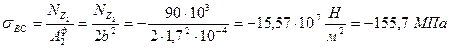 (уравнение константы).
(уравнение константы).
Так как все сечения в пределах участка ВС равноопасны, то σВС = σmaxр.
Выполним проверку условия прочности:

155,7 МПа < 160 МПа.
Недогрузка стержня на участке ВС составляет:
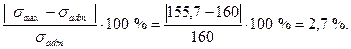
Недогрузка не превышает 5 %, следовательно, условие прочности на участке ВС выполняется.
Участок АВ (0 ≤ z1 ≤ 0,1 м )
Определим нормальные напряжения при назначенных размерах поперечного сечения стержня на участке АВ, учитывая, что фактическая площадь поперечного сечения определяется по формуле  :
:
 (уравнение константы).
(уравнение константы).
Так как все сечения в пределах участка равноопасны, то σАВ = σmaxр.
Выполним проверку условия прочности:
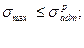
138,4 МПа < 160 МПа.
Недогрузка стержня на участке АВ составляет:
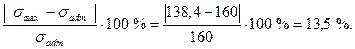
Участок СD (0 ≤ z3 ≤ 0,3 м )
Участок СD по условию задачи имеет круглое сплошное поперечное сечение диаметром d.
Требуемая площадь поперечного сечения из условия прочности равна:

Площадь сплошного круглого сечения определяется по формуле:

Откуда находим, что

Назначаем d = 2,2 см.
Определим нормальные напряжения при назначенных размерах поперечного сечения стержня на участке СD, учитывая, что фактическая площадь поперечного сечения определяется по формуле 
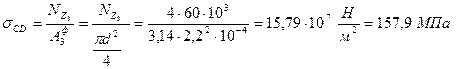 (уравнение константы).
(уравнение константы).
Так как все сечения в пределах участка равноопасны, то σСD = σmaxр.
Выполним проверку условия прочности:

157,9 МПа < 160 МПа.
Недогрузка стержня на участке СD составляет:
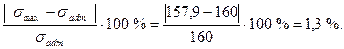
Недогрузка не превышает 5 %, следовательно, условие прочности на участке СD выполняется.
По найденным значениям нормальных напряжений на каждом участке строим эпюру распределения нормальных напряжений σ по длине стержня (рисунок 3.2, в).
Для опасных сечений строим эпюру распределения нормальных напряжений по сечению (рисунок 3.2, г). Участок ВС более нагружен, чем участок АВ, следовательно, любое сечения на участке ВС более опаснее; поэтому эпюра распределения нормальных напряжений по высоте поперечного сечения строится на этом участке.
Из эпюры нормальных напряжений по длине стержня следует, что наибольшие нормальные напряжения возникают на участке СD:

Условие прочности стержня выполняется:
157,9 МПа <160 МПа.








