Колебания прямоугольной мембраны.
мембрана, которая в состоянии покоя имеет форму прямоугольника, ограниченного прямыми x=0, x=l, y=0, y=m.
Уравнение колебаний мембраны 
Начальные условия
Граничные условия
будем искать решение в виде произведения трех функций, каждая из которых зависит только от одного аргумента:
Из граничных условий следует, что
X(0)=0, X(l)=0, Y(0)=0, Y(m)=0 
, 
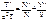
для функции X(x) получаем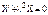 
, 
Для функции Y(y) 
, Y(0)=Y(m)=0
Для функции T(t) 
Решение имеет вид 
Из краевого условия X(0)=X(l)=0 находим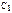 
= 0 и
, где k – целое число
Аналогично, из Y(0)=Y(m)=0 находим 
= 0 и
, где n – целое число
В результате получаем собственные числа и собственные функции
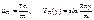
Уравнение для функции T(t) принимает вид:
Решение этого уравнения имеет вид:
Здесь 
- собственные частоты колебаний мембраны. Таким образом, частное решение уравнения колебаний прямоугольной мембраны имеет вид
Оно может быть приведено к виду
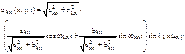
Где 
, 
Отсюда видно, что каждая точка мембраны с координатами (x,y) совершает простое гармоническое колебание с частотой 
и амплитудой 
. Все точки колеблются в одной фазе. Точки, координаты которых удовлетворяют уравнениям 
, 
Общее решение задачи о колебаниях мембраны представляется как сумма частных
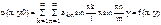
Колебания круглой мембраны.
Введем полярные координаты r и φ: x=rcos φ, y=rsin φ.
Выполняя замену переменных u(x,y,t) à u(r,φ,t) уравнение колебаний мембраны приводятся к виду
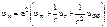
Граничные условие будет иметь вид 
Начальные условия
Будем рассматривать только осесимметричные колебания мембраны, т.е. начальные условия не должны зависеть от угла φ. Очевидно, что в любой момент времени скорости и отклонения точек будут зависеть от угла,
Граничные условия 
Начальные условия 
Будем искать решение в виде 
Из краевого условия сразу находим U(R)=0
В результате приходим к уравнениям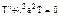 
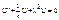делаем замену 
:
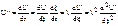
Найдем решение уравнения 
Записываем ряд: 
Где l=2,3…
Предполагая, что 
, находим
находим, что 
=0. преобразуем l-е уравнение
С учетом найденного =0
все нечетные коэффициенты равны нулю.
при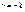 
решение обращается в бесконечностьпри x=0. 
. В результате, для четных коэффициентов получаем
Применяя эту формулу m-1 раз, получим
Получаем
полученное решение 
функция Бесселя первого рода k-ого порядка и имеет вид:
В случае γ = -k
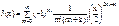
Деля замену m=k+n, n=0,1,2…., получаем
представляет собой другое, линейно независимое от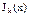 
, решение, только в случае нецелых k. 
Из граничного условия u(R,t) =0 получаем U(R) = 0, отсюда находим собственные числа задачи
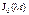=0 Которыми будут являться величины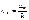 
Где 
- нули Бесселя – корни уравнения 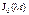=0
u(r,t)=U(r)T(t) U(R)T(t)=0 U(R)=0 
=0 
=0
решаем уравнения для функции Т:
получаем собственные функции
Сумма собственных функций
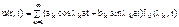
Коэффициенты 
и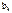 
подбираем так, чтобы удовлетворить начальным условиям
В последних равенствах сделаем замену переменных x = r/R:
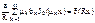
Для нахождения коэффициентов и 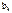надо использовать условие ортогональности функций 
:
А также соотношение 
k=n 
С учетом этого находим
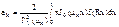
Уравнения параболического типа.
Линейная задача о распространении тепла.
стержень будем считать настолько тонким, что в каждый момент времени температуры всех точек в одном поперечном сечении будут одинаковы. Пусть стержень располагается вдоль оси x, тогда u(x,t)–температура в сечении стержня с абсциссой x в момент времени t.
будет определять скорость изменения температуры вдоль оси x. Количество тепла 
, которое необходимо сообщить однородному телу, чтобы повысить его температуру на 
, равно 
Где c–удельная теплоемкость тела, 
–плотность тела, V –объем тела.
Здесь k – коэффициент теплопроводности.
Рассмотрим участок стержня, ограниченный поперечными сечениями с координатами x и x+ 
. Количество тепла, проходящее через левое поперечное сечение:
Для нахождения тепла, проходящего через правое поперечное сечение с точностью до бесконечно малых высших порядков,
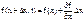Пусть 
Тогда находим
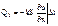
Количество теплоты, сообщенное выбранному участку стержня за время 
: 
С другой стороны, 
Введем обозначение 
Получаем уравнение теплопроводности для однородного стержня без тепловых источников
Здесь 
– коэффициент температуропроводности. F(x,t) – плотность тепловых источников – количество теплоты, выделяющееся (или поглощающееся) в единицу времени на единице длины. 
Отсюда
