Виды имитационного моделирования.

Агентное моделирование

Дискретно-событийное моделирование

Системная динамика

Некоторые области применения имитационного моделирования: бизнес-процессы, боевые действия, динамика населения, дорожное движение, ИТ-инфраструктура, управление проектами, экосистемы. Популярные компьютерные системы имитационного моделирования: AnyLogic,Aimsun,Arena,eM-Plant,Powersim,GPSS.Имитационное моделирование позволяет имитировать поведение системы во времени. Причем плюсом является то, что временем в модели можно управлять: замедлять в случае с быстропротекающими процессами и ускорять для моделирования систем с медленной изменчивостью. Можно имитировать поведение тех объектов, реальные эксперименты с которыми дороги, невозможны и опасны.

№86. Под математической моделью (ММ) понимается оператор, характеризующий поведение реальной системы и отражающий все ее информационные свойства. В соответствии с этим определением выделяются наиболее существенные свойства и признаки системы, они представляются в такой форме, которая необходима для последующего теоретического и экспериментального исследования.

На первом этапе расчета и проектирования систем автоматического управления (САУ) ограничиваются качественным описанием систем и в связи с этим рассматривают их функциональные схемы. Такое описание называют содержательным или неформальным. Неформальным описанием САУ называется вся имеющаяся совокупность сведений о ней, достаточная для построения фактического алгоритма ее работы. Неформальное описание системы содержит информацию, достаточную для построения ее функциональной схемы. Последняя же служит основой для разработки формального (математического) описания системы.

Недостаток содержательного или неформального описания систем в том, что такой подход не оперирует количественными характеристиками и, таким образом, наука, в основе которой лежит неформальное описание, не является точной наукой. Для решения же задач исследования и проектирования систем необходимо оперировать количественными характеристиками, определяющими качество ее работы. А именно, математическими моделями. В связи с этим центральным понятием теории систем управления является математическая модель или оператор системы.

Пользуясь понятием системного оператора, можно на единой основе рассмотреть понятие математической модели САУ.

Пусть 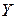и 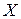— множества входных и выходных сигналов САУ. Если каждому элементу 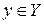ставится в соответствие определенный элемент 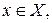то говорят, что задан системный оператор

Связь между входом и выходом системы задается посредством системного оператора 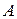[2]:

и .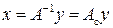

Операторное уравнение (или уравнение с оператором 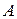) следует считать математической моделью САУ, поскольку оно устанавливает количественную связь между входом 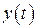и выходом 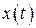системы.

Принципиально важным является ответ на вопрос: как построить оператор системы и, таким образом, определить ее математическую модель. Ответ на поставленный вопрос состоит в следующем: математические модели могут быть представлены разными математическими средствами, но важнейшую роль играют дифференциальные и интегральные уравнения, которые получаются на основании фундаментальных физических законов, лежащих в основе функционирования механических, электрических, гидравлических,термодинамических систем.

Для получения дифференциального уравнения системы в целом обычно составляют описание ее отдельных элементов, т.е. составляют дифференциальные уравнения для каждого входящего в систему элемента (например, для САУ (рис. 1.1) составляются дифференциальные уравнения усилителя, привода, реостата, электрической печи, термопары и элемента сравнения).

Совокупность всех уравнений элементов и дает уравнение системы в целом. Уравнения системы определяют ее математическую модель, которая для одной и той же системы в зависимости от цели исследования может быть разной.

Полезно при решении одной и той же задачи на разных этапах строить разные математические модели: начинать проектирование можно с простой модели, а затем ее постепенно усложнять, с тем, чтобы учесть дополнительные физические явления и связи, которые на начальном этапе не были учтены как несуществующие.

Математические модели обычно быть представляются с помощью дифференциальных, интегральных или разностных уравнений [1]. Для класса линейных систем управления математические модели представляются с использованием передаточных функций и импульсных переходных функций. Каждая форма представления математических моделей имеет свои области применения, свои преимущества, свои достоинства.

№87. MathCAD является математическим редактором, позволяющим проводить разнообразные научные и инженерные расчеты, начиная от элементарной арифметики и заканчивая сложными реализациями численных методов.

MATLAB - В пакет входит множество хорошо проверенных численных методов (решателей), операторы графического представления результатов, средства создания диалогов. Отличительной особенностью MATLAB по сравнению с обычными языками программирования является матричное представление данных и большие возможности матричных операций над данными

Математическое моделирование включает следующие шаги:

1) выбор расчетной схемы и определение необходимой детализации;
2) математическое описание (составление системы уравнений);
3) выбор метода решения;
4) приведение модели (включающей уравнения, метод, исходные данные и начальные условия) к виду, удобному для решения на ЭВМ;
5) составление программы для ЭВМ;
6) проведение расчетов (моделирование);
7) анализ результатов;
8) оформление отчета (описание, схемы, рисунки, графики, формулы);

Имитационное моделирование (ситуационное моделирование) — метод, позволяющий строить модели, описывающие процессы так, как они проходили бы в действительности. Такую модель можно «проиграть» во времени как для одного испытания, так и заданного их множества. При этом результаты будут определяться случайным характером процессов. По этим данным можно получить достаточно устойчивую статистику.

№88. Эффективность использования экспериментальных ресурсов при математическом моделировании существенным образом зависит от выбора плана эксперимента. Причин этого две:

- план эксперимента в значительной степени определяет порядок статистического анализа его результатов;

- успешность разрешения с помощью эксперимента поставленных экспериментатором вопросов существенно зависит от его плана.

Основная цель моделирования состоит в возможно более глубоком изучении поведения моделируемой системы при минимальных затратах. С этой целью необходимо планировать и проектировать не только саму модель, но и процесс ее использования, то есть проведения на ней экспериментов.

Итак, основная задача планирования машинных экспериментов – получение необходимой информации об исследуемой системе при ограничениях на ресурсы. К числу частных задач, решаемых при планировании машинных экспериментов, относятся задачи уменьшения затрат машинного времени на моделирование, увеличения точности и достоверности результатов моделирования, проверки адекватности модели и т.д.

Важное значение при планировании эксперимента имеют следующие обстоятельства:

- простота повторения условий эксперимента на ПК с моделью;

- возможность управления экспериментом, включая его прерывание и возобновление;

- легкость варьирования условий (воздействий внешней среды;

- наличие корреляции между последовательностью точек в процессе моделирования.

Преимуществом машинных экспериментов перед натурными является возможность полного воспроизведения условий эксперимента с моделью. Сравнивать две альтернативы возможно при одинаковых условиях, что достигается, например, выбором одной и той же последовательности случайных чисел для каждой из альтернатив.

Существенным достоинством является также простота прерывания и возобновления машинных экспериментов, что позволяет применять последовательные и эвристические приемы планирования, которые могут оказаться нереализуемыми в экспериментах с реальными объектами.

№89. Методика выполнения измерений (МВИ) – это совокупность метода, технических средств и правил подготовки и проведения измерений, обработки и представления результатов (сокращенно – правила измерений).

Правила измерений – это комплекс требований к содержанию, последовательности и условиям выполнения всех операций (действий), обеспечивающих полное решение данной измерительной задачи, т.е. получение информации об измеряемой величине определенным методом с помощью определенных технических средств и представление этой информации в удобной для дальнейшего использования форме.

К техническим средствам, являющимся вторым элементом МВИ, относятся как собственно средства измерений, так и вспомогательные устройства, необходимые для подготовки и выполнения измерений, обеспечения определенных условий и режимов измерений (например, термостатирующие и экранирующие устройства, каналы связи, виброгасители, средства автоматизированной обработки и т.п.).

Третий элемент МВИ – метод измерений. Это понятие часто путают то с (более частным) физическим принципом измерений, то с (более общим) методикой выполнения измерений.

Принцип измерений – это, по существу, физическое явление, реализация которого в процессе измерений позволяет сформировать определенный информативный параметр, значения которого связаны со значениями измеряемой величины (при прямых измерениях – это информативный параметр самой измеряемой величины), и зафиксировать его чувствительным элементом применяемого средства измерений. Например, измерение температуры с помощью ртутного термометра основано на явлении термического расширения столбика ртути под воздействие измеряемой температуры. Следовательно, явление термического расширения ртути и является в данном случае физическим принципом измерения температуры. Совокупность приемов использования принципов и средств измерений называется методом измерений.

Для прямых измерений, где физический принцип, как правило, однозначно определяется принципом действия измерительного прибора, совокупность методических приемов (описание метода) носит метрологический характер. Такие общие метрологические приемы, называемые методами прямых измерений (например, метод непосредственной оценки, нулевой метод, дифференциальные или разностные методы), позволяют в ряде случаев исключить (или компенсировать) наиболее существенные систематические погрешности измерений.

Методы косвенных измерений, как правило, отражают в своем названии физический принцип, на котором они основаны, и содержат (в нормативно-описательном плане) большой комплекс технических приемов его использования. Например, метод измерения расхода жидкостей по переменному перепаду давлений характеризуется большим комплексом технических приемов (простое описание их в расходоизмерительной литературе занимает не один десяток страниц) создания в потоке жидкости перепада давлений, пропорционального средней скорости потока, использования рабочей формулы измерений (выбора стандартизованных значений коэффициентов расхода сужающих устройств и различных поправочных множителей), измерений входящих в эту формулу величин (перепада давлений, плотности, относительной площади сужающего устройства и др.). И, несмотря на столь большой набор основополагающих принципов и пра-вил, это еще не методика измерений расхода методом переменного пере-пада давлений. Последняя, кроме отмеченного, должна включать в себя требования к монтажу, эксплуатации и контролю сужающих устройств конкретных (используемых в МВИ) типов, к условиям выполнения изме-рений, к оценке погрешности измерений в данных условиях.

Разработка и аттестация МВИ – это, по существу, единственный путь гарантированного обеспечения требуемой точности массовых технических измерений, выполняемых при производстве, испытаниях и контроле качества продукции. Это обусловливается ниже описанными причинами.

Основной особенностью современного развития техники измерений является все большее внедрение в измерительную практику косвенных методов измерений, основанных на вновь открытых физических явлениях и закономерностях (атомно-молекулярные явления, фазовые переходы, ультразвук, лазеры и др.) и позволяющих обеспечить высокую разрешающую способность и точность, большие диапазоны измерений там, где прямые методы не позволяют этого сделать.

При этом определяющим точность выполняемых измерений фактором становятся методические погрешности, обусловленные неполнотой рабочих уравнений, описывающих зависимости косвенно измеряемых величин от количественных характеристик физических явлений и процессов (положенных в основу методов измерений), непостоянством теоретических или эмпирических коэффициентов этих уравнений при изменении свойств измеряемых объектов, режимов и условий измерений, что усугубляется постоянным ужесточением режимов и условий измерений (высокие и низкие температуры, электрические и магнитные поля, вибрация и др.) в производстве и невозможностью их воспроизведения при градуировке и поверке используемых средств измерений.

Кроме того, при использовании для косвенных измерений сложных многоблочных систем и комплексов все большее влияние на формирование общей погрешности измерений оказывают характеристики вспомогательных устройств (линий связи, систем подготовки измерений и др.).

В таких условиях вклад погрешностей собственно измерительных устройств в суммарную погрешность измерений становится меньше. Например, для такого распространенного вида измерений, как измерение массы движущихся объектов, погрешность применяемых средств измерений составляет лишь 5-6 % от суммарной погрешности результата взвешивания. Остальную часть составляют методические погрешности, погрешности, вносимые работой вспомогательных устройств, обусловленные динамикой процесса измерений. Причем данные методические погрешности (как и любые методические погрешности) не могут быть выявлены и оценены в процессе выполнения измерений, обработки из результатов.

Разработка МВИ включает в себя следующие основные этапы:

1) выбор (или разработка, если таковые отсутствуют) метода и средств измерений;

2) разработка измерительной схемы, устанавливающей функциональные взаимосвязи между объектом измерений, средствами измерений и вспомогательными техническими устройствами, необходимыми для осуществления процесса измерений, обеспечения условий и режимов измерений;

3) разработка процедуры измерений – комплекса требований к содержанию, последовательности и условиям выполнения операций, необходимых для получения конечного результата, являющегося целью решения измерительной задачи (данные требования должны охватывать все аспекты измерительного процесса, в том числе, его безопасность и связь с операторами, выполняющими измерения);

4) разработка проектов нормативных документов, регламентирующих МВИ.

МВИ могут быть оформлены в виде следующих нормативно-техни-ческих документов:

– стандарт (ГОСТ, СТО) типовой МВИ;

– аттестат МВИ;

– разделов стандартов ТУ, технологических процессов, методов испытаний и контроля продукции.

Метрологическая аттестация МВИ – это исследования, направленные на оценку максимально возможных погрешностей измерений, которые могут и будут выполняться по данной МВИ (методом, средствами и по правилам, регламентированным нормативным документом на МВИ). В зависимости от сложности решаемых измерительных задач, сложности используемых методов измерений находят применение три различных способа аттестации МВИ – расчетный, расчетно-экспериментальный и экспериментальный.

Расчетный способ аттестации МВИ применим для простейших (как правило, прямых) измерений, характеристики погрешности которых практически целиком определяются нормированными в технической документации на применяемые средства измерений (ТУ, паспорт, инструкция по эксплуатации) значениями его метрологических характеристик. В данном случае погрешность измерений целиком определяется инструментальной составляющей (методические составляющие отсутствуют или пренебрежительно малы), и нормированных в технической документации на применяемое средство измерений метрологических характеристик достаточно для достоверных оценок этой (инструментальной) составляющей.

Типичными составляющими инструментальной погрешности измерений являются: основная, дополнительные и динамическая погрешности средства измерений, а также погрешность, обусловленная его взаимодействием с объектом измерений. Следовательно, расчетная аттестация МВИ сводится к определению (по четырем составляющим) максимально возможного для заданных условий измерений интервала, в котором с заданной вероятностью лежат практически реализующиеся значения погрешности измерений.

В тех случаях, когда нормированных в технической документации на средства измерений метрологических характеристик недостаточно для достоверных оценок реальной точности измерений, выполняемых по аттестуемой МВИ (например, велик уровень методических погрешностей или в технической документации не хватает данных для оценки каких-либо составляющих инструментальной погрешности), а экспериментальную проверку точности измерений осуществить технически невозможно (или нецелесообразно), используют расчетно-экспериментальный способ аттестации МВИ.

Для нахождения суммарных оценок характеристик погрешности измерений, выполняемых по аттестуемой таким способом МВИ, т.е. для статистического суммирования частных погрешностей (оцененных экспериментально или расчетом) необходимо в процессе аттестации группировать их по статистическим свойствам на систематические и случайные. Как показывает практика, это сложная задача. Поэтому можно рекомендовать проводить деление погрешностей на систематические и случайные по такому формальному признаку, как возможность их частичной компенсации усреднением результатов многократных измерений, выполняемых за достаточно малый (допускаемый по условиям измерений) промежуток времени. Если такая компенсация возможна, то погрешность относится к случайной, если нет – к систематической.

Суть экспериментального способа аттестации МВИ заключается в прямом непосредственном сравнении результатов измерений, выполняемых (одновременно и в тех же условиях) при помощи более точных (образцовых) методов и средств. Там, где такие методы и средства имеются, где целесообразно и технически возможно их применить, наилучшим является экспериментальный способ аттестации МВИ.

По результатам аттестации оформляется научно-технический отчет и аттестат МВИ, в котором указываются:

– назначение и область применения МВИ;

– типы и номера экземпляров средств измерений и технические характеристики вспомогательных устройств;

– описание метода измерений;

– алгоритм операций подготовки и выполнения измерений;

– числовые значения характеристик погрешности измерений;

– межповерочные интервалы и НТД, по которым следует проводить поверку средств измерений (или контроль точности измерений);

– требования к квалификации операторов.

Существенное отличие между расчетным, расчетно-эксперимен-тальным и экспериментальным способами аттестации МВИ заключается в следующем – расчетная аттестация проводится на основе анализа НТД, расчетно-экспериментальная и экспериментальная – проводятся на конкретных реализациях измерительной схемы (реально воплощенной в соответствии с требованиями МВИ, на конкретных экземплярах используемых приборов) в реальных производственных (или имитирующих их) условиях.

№90. Оптимизация – это процесс нахождения наилучшего решения задачи, определяемого по некоторому заранее установленному критерию. Другими словами, это целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих условиях.