Построение изображения додекаэдра
Операции проецирования, понятие проекции. Виды проекций. Аксонометрические проекции. Изометрические проекции.
Отображение некоторого множества точек S пространства Rn на другое пространство Rm той же или меньшей размерности называется проецированием S на Rm, а полученный образ - проекцией S
Частным случаем проецирования является изображение трехмерного объекта на плоскости.
Если центром проецирования является бесконечно удаленная (несобственная) точка, лучи проецирующего пучка параллельны и проекция называется параллельной
Если же в качестве центра проецирования выбирается собственная точка пространства R3, то проекция называется центральной (перспективной), а проецирующий пучок лучей является расходящимся.
Виды параллельных проекций:
В зависимости от расположения картинной плоскости и координатных осей параллельные проекции делятся на
1) ортографические,
2) аксонометрические,
3) косоугольные
В первых двух случаях пучок параллельных лучей перпендикулярен картинной плоскости, а в 3-м случае направлен под произвольным углом к ней
Изометрическая проекция
В этом случае все три проекции единичных ортов равны между собой, что приводит к равенствам:
cos2 ψ + sin2 φ * sin2 ψ = cos2 φ
sin2 ψ + sin2 φ * cos2 ψ = cos2 φ
Откуда следует, что
sin2 φ = 1/3, sin2 ψ = 1/2.
Стандартная изометрическая проекция:
Соответствует выбору ψ = π/4
В этом случае матрица проецирования принимает вид:
0,707 -0,408 0 0
М= 0 0,816 0 0
-0,707 -0,408 0 0
0 0 0 1
| 6) Операции проецирования, понятие проекции. Виды проекций. Аксонометрические проекции. Триметрические проекции.
Отображение некоторого множества точек S пространства Rn на другое пространство Rm той же или меньшей размерности называется проецированием S на Rm, а полученный образ - проекцией S
Частным случаем проецирования является изображение трехмерного объекта на плоскости.
Если центром проецирования является бесконечно удаленная (несобственная) точка, лучи проецирующего пучка параллельны и проекция называется параллельной
Если же в качестве центра проецирования выбирается собственная точка пространства R3, то проекция называется центральной (перспективной), а проецирующий пучок лучей является расходящимся.
Виды параллельных проекций:
В зависимости от расположения картинной плоскости и координатных осей параллельные проекции делятся на
1) ортографические,
2) аксонометрические,
3) косоугольные
В первых двух случаях пучок параллельных лучей перпендикулярен картинной плоскости, а в 3-м случае направлен под произвольным углом к ней
Аксонометрические проекции
При аксонометрическом проецировании картинная плоскость не совпадает ни с одной из координатных плоскостей ОСК
В соответствии со взаимным расположением картинной плоскости и координатных осей объектной системы координат различают три вида аксонометрических проекций
Виды аксонометрических проекций:
1)Триметрическая проекция – нормальный вектор картинной плоскости образует с ортами координатных осей ОСК попарно различные углы.
2) Диметрическая проекция – два из трех указанных углов равны.
3) Изометрическая проекция – все углы равны.
Построение аксонометрической проекции:
Любая аксонометрическая проекция может быть получена комбинацией поворота до совмещения нормали к картинной плоскости с одной из координатных осей ОСК и последующего ортографического проецирования:
M=P*R
Например, при повороте на угол Ψ вокруг оси Y, повороте на угол φ вокруг оси X и последующем проецировании вдоль оси Z матрица преобразования имеет вид:
cosψ sinφ *sin ψ 0 0
М= 0 cos φ 0 0
sin ψ –sinφ *cos ψ 0 0
0 0 0 1
Эта матрица получается в результате перемножения трех матриц – Ry, Rx и Pz:
M = Pz* Ry * Rx
Триметрическая проекция:
При таком проецировании единичные орты координатных осей преобразуются следующим образом:
ex*M=(1 0 0 1)*M=(cosψ, sinφ *sin ψ, 0, 1)
ey*M=(0 1 0 1)*M=(0, cosφ, 0, 1)
ez*M=(0 0 1 1)*M=(sinψ, -sinφ *sin ψ, 0, 1)
9) Операции проецирования, понятие проекции. Виды проекций. Косоугольные проекции.
Отображение некоторого множества точек S пространства Rn на другое пространство Rm той же или меньшей размерности называется проецированием S на Rm, а полученный образ - проекцией S
Частным случаем проецирования является изображение трехмерного объекта на плоскости.
Если центром проецирования является бесконечно удаленная (несобственная) точка, лучи проецирующего пучка параллельны и проекция называется параллельной
Если же в качестве центра проецирования выбирается собственная точка пространства R3, то проекция называется центральной (перспективной), а проецирующий пучок лучей является расходящимся.
Виды параллельных проекций:
В зависимости от расположения картинной плоскости и координатных осей параллельные проекции делятся на
1) ортографические,
2) аксонометрические,
3) косоугольные
В первых двух случаях пучок параллельных лучей перпендикулярен картинной плоскости, а в 3-м случае направлен под произвольным углом к ней
Косоугольные проекции:
При косоугольном проецировании пучок проецирующих лучей не перпендикулярен картинной плоскости. Косоугольные проекции сочетают в себе свойства ортографических и аксонометрических проекций.
При косоугольном проецировании орта ez на плоскость XY имеем:
(0, 0, 1, 1)g(α, β, 0, 1)
Матрица соответствующего преобразования имеет вид:
1 0 0 0
0 1 0 0
α β 0 0
0 0 0 1
Виды косоугольных проекций:
Выделяют два вида косоугольных проекций:
свободную,
кабинетную.
В случае свободной проекции угол наклона проецирующего пучка к картинной плоскости равен π/4 и, соответственно
α = β = cos π/4.
Кабинетная проекция является частным случаем свободной проекции – масштаб по оси Z вдвое меньше. Тогда
α = β = 0,5*cos π/4.
| 7) Операции проецирования, понятие проекции. Виды проекций. Аксонометрические проекции. Диметрические проекции.
Отображение некоторого множества точек S пространства Rn на другое пространство Rm той же или меньшей размерности называется проецированием S на Rm, а полученный образ - проекцией S
Частным случаем проецирования является изображение трехмерного объекта на плоскости.
Если центром проецирования является бесконечно удаленная (несобственная) точка, лучи проецирующего пучка параллельны и проекция называется параллельной
Если же в качестве центра проецирования выбирается собственная точка пространства R3, то проекция называется центральной (перспективной), а проецирующий пучок лучей является расходящимся.
Виды параллельных проекций:
В зависимости от расположения картинной плоскости и координатных осей параллельные проекции делятся на
1) ортографические,
2) аксонометрические,
3) косоугольные
В первых двух случаях пучок параллельных лучей перпендикулярен картинной плоскости, а в 3-м случае направлен под произвольным углом к ней
Диметрическая проекция
Равенство углов между нормалью к картинной плоскости и двумя координатными осями означает равенство проекций соответствующих ортов
Например, равенство углов нормали с осями абсцисс и ординат означает, что:
cos2 ψ + sin2 φ * sin2 ψ = cos2 φ
Отсюда следует, что
sin2 ψ = tg2 φ
Теперь углы поворота вокруг осей ординат и абсцисс уже не являются независимыми и задание одного из них определяет возможные значения другого угла
Так, для ψ=π/4 угол φ может иметь значения, равные ± arctg (√1/2)
Аналогичным образом могут быть рассмотрены две другие диметрические проекции, соответствующие другим возможным выборам пар равных углов
Вводится понятие стандартной диметрической проекции, при которой длины проекций единичных ортов на картинную плоскость находятся в отношении 2: 2: 1
Тогда из условий
sin2 ψ = tg2 φ
и
cos2 φ = 4*(sin2 ψ + sin2 φ * cos2 ψ)
получим
tg2 φ = 1/8,
что приблизительно соответствует углам
φ = ± 19,5° и ψ = ± 20,7°
В случае, когда единичный вектор нормали к картинной плоскости лежит в 1-м октанте, φ > 0 и ψ < 0 и матрица диметрического проецирования равна:
0,935 -0,118 0 0
М= 0 0,943 0 0
-0,354 -0,312 0 0
0 0 0 1
10) Этапы построения изображений трехмерных тел. Платоновы тела. Виды платоновых тел.
Трехмерная графика
В трехмерном случае объекты, описанные в мировых координатах, отсекаются по границе видимого объема, а после этого должны быть отображены в окне вывода на экране дисплея
Сложность состоит в том, что экран дисплея не имеет третьего измерения
Решение проблемы достигается путем введения проекций, которые отображают трехмерные объекты на двумерной проекционной картинной плоскости (КП)
В процессе вывода трехмерной графической информации задается видимый объем в мировом пространстве, его проекция на КП и окно вывода на экране дисплея
В общем случае объекты, определенные в трехмерном мировом пространстве, отсекаются по границам трехмерного видимого объема и после этого проецируются
При этом видимый объем преобразуется в видимое окно, которое затем отображается на экране дисплея
Картинная плоскость определяется некоторой точкой на плоскости, которую будем называть опорной точкой (ОТ) и нормалью к картинной плоскости (НКП)
КП может произвольным образом располагаться относительно проецируемых объектов, заданных в мировых координатах. Она может пересекать их, проходить впереди или позади объектов
Платоновы тела:
Платоновыми телами называются правильные многогранники, т.е. такие выпуклые многогранники, все грани которых суть правильные многоугольники и все многогранные углы при вершинах равны между собой
Евклидом было доказано, что существует всего пять правильных многогранников, каждый из которых характеризуется числом углов у каждой грани n и числом граней, примыкающих к одной вершине m
Формула Эйлера:
Г – Р + В = 2,
где Г – число граней, Р – число ребер, В – число вершин
Согласно Евклиду существуют следующие платоновы тела:
n = 3, m = 3 – тетраэдр;
n = 4, m = 3 – гексаэдр (куб);
n = 3, m = 4 – октаэдр;
n = 3, m = 5 – икосаэдр;
n = 5, m = 3 – додекаэдр
Изображение многогранников:
Для построения любого многогранника необходимо:
- задать координаты его вершин;
- для каждой из граней задать множество принадлежащих ей вершин;
- соединить отрезками прямых вершины каждой из граней
Полученное таким образом изображение многогранника называется каркасным и примеры таких изображений имеются на предыдущем слайде
Одной из проблем при построении таких изображений является выделение видимых и невидимых ребер, причем последние принято изображать штриховыми линиями
|
|
11) Платоновы тела. Построение изображения тетраэдра.
Прежде всего заметим, что любое из платоновых тел может быть вписано в некоторый куб
Куб – это тело с высокой степенью симметрии, что значительно облегчает дальнейший процесс построения изображения
Будем считать, что начало координат находится в центре куба, описанного вокруг многогранника, и что длина ребра куба равна 2
Тетраэдр
Тетраэдр имеет 4 грани, 6 ребер и 4 вершины. Простейший способ построения тетраэдра заключается в использовании куба в качестве вспомогательного тела, как показано на рис. 5. Сначала вычерчивается куб, выбираются нужные грани, проводятся диагонали, а затем лишние линии куба стираются. При желании куб можно поворачивать на требуемый угол.
13)Платоновы тела:/ Икосаэдр
Платоновыми телами называются правильные многогранники, т.е. такие выпуклые многогранники, все грани которых суть правильные многоугольники и все многогранные углы при вершинах равны между собой
Евклидом было доказано, что существует всего пять правильных многогранников, каждый из которых характеризуется числом углов у каждой грани n и числом граней, примыкающих к одной вершине m
Формула Эйлера:
Г – Р + В = 2,
где Г – число граней, Р – число ребер, В – число вершин
Согласно Евклиду существуют следующие платоновы тела:
n = 3, m = 3 – тетраэдр;
n = 4, m = 3 – гексаэдр (куб);
n = 3, m = 4 – октаэдр;
n = 3, m = 5 – икосаэдр;
n = 5, m = 3 – додекаэдр
Икосаэдр
Икосаэдр – это многогранник, имеющий 20 граней, 30 ребер и 12 вершин. Для его построения необходимо выполнить следующие операции:
1) построить правильный пятиугольник на одной из граней единичного куба;
2) построить правильный пятиугольник на противоположной грани того же куба;
3) соединить вершины нижнего многоугольника с вершинами верхнего многоугольника;
4) вычислить z-координаты верхней и нижней точек икосаэдра и соединить их с вершинами верхнего и нижнего многоугольников, соответственно.
| Платоновы тела:/ Гексаэдр (куб)
Платоновыми телами называются правильные многогранники, т.е. такие выпуклые многогранники, все грани которых суть правильные многоугольники и все многогранные углы при вершинах равны между собой
Евклидом было доказано, что существует всего пять правильных многогранников, каждый из которых характеризуется числом углов у каждой грани n и числом граней, примыкающих к одной вершине m
Формула Эйлера:
Г – Р + В = 2,
где Г – число граней, Р – число ребер, В – число вершин
Согласно Евклиду существуют следующие платоновы тела:
n = 3, m = 3 – тетраэдр;
n = 4, m = 3 – гексаэдр (куб);
n = 3, m = 4 – октаэдр;
n = 3, m = 5 – икосаэдр;
n = 5, m = 3 – додекаэдр
Гексаэдр (куб)
Гексаэдр имеет 6 граней, 12 ребер и 8 вершин. Построение этого тела тривиально и не вызывает проблем.
Исходная матрица координат вершин (вершины 0, 1, 2, 3 – нижнее основание; вершины 4, 5, 6, 7 – верхнее основание).
|
| x
| y
| z
|
| |
|
| -1
| -1
|
| |
| -1
| -1
| -1
|
| |
| -1
|
| -1
|
| |
|
|
| -1
|
| |
|
| -1
|
|
| |
| -1
| -1
|
|
| |
| -1
|
|
|
| |
|
|
|
|
|
Платоновы тела: / додик
Платоновыми телами называются правильные многогранники, т.е. такие выпуклые многогранники, все грани которых суть правильные многоугольники и все многогранные углы при вершинах равны между собой
Евклидом было доказано, что существует всего пять правильных многогранников, каждый из которых характеризуется числом углов у каждой грани n и числом граней, примыкающих к одной вершине m
Формула Эйлера:
Г – Р + В = 2,
где Г – число граней, Р – число ребер, В – число вершин
Согласно Евклиду существуют следующие платоновы тела:
n = 3, m = 3 – тетраэдр;
n = 4, m = 3 – гексаэдр (куб);
n = 3, m = 4 – октаэдр;
n = 3, m = 5 – икосаэдр;
n = 5, m = 3 – додекаэдр
Построение изображения додекаэдра
Этот многогранник имеет 12 граней, 30 ребер, 20 вершин. Каждая из 12 граней является правильным пентагоном (пятиугольником).
Конструирование додекаэдра удобно выполнять с помощью вписанного в него куба (рис. 8) Этот метод конструирования был предложен Евклидом.
На каждой грани куба строим «четырехскатную крышу», две грани которой – треугольники и две – трапеции. Такой треугольник и трапецию получим, если построим правильный пятиугольник, у которого диагональ равна ребру куба. Стороны этого пятиугольника будут равны ребрам додекаэдра, а построенные с помощью диагонали треугольник и трапеция окажутся фрагментами «четырехскатной крыши»
| 12) Платоновы тела:/ Октаэдр
Платоновыми телами называются правильные многогранники, т.е. такие выпуклые многогранники, все грани которых суть правильные многоугольники и все многогранные углы при вершинах равны между собой
Евклидом было доказано, что существует всего пять правильных многогранников, каждый из которых характеризуется числом углов у каждой грани n и числом граней, примыкающих к одной вершине m
Формула Эйлера:
Г – Р + В = 2,
где Г – число граней, Р – число ребер, В – число вершин
Согласно Евклиду существуют следующие платоновы тела:
n = 3, m = 3 – тетраэдр;
n = 4, m = 3 – гексаэдр (куб);
n = 3, m = 4 – октаэдр;
n = 3, m = 5 – икосаэдр;
n = 5, m = 3 – додекаэдр
Октаэдр
Октаэдр имеет 8 граней, 12 ребер и 6 вершин и не может быть непосредственно вписан в куб. Однако, алгоритм его построения достаточно прост. Рассмотрим внимательно рис.6. Как видно, две вершины октаэдра расположены по обе стороны квадрата. Предположим, что стороны квадрата 1-2-3-4 имеют длину, равную 2. Точка 7 расположена в центре квадрата и также является центром октаэдра, а точка 8 находится посередине ребра 4-1. Поскольку точка 5 лежит на перпендикуляре в точке 7, то все, что нам надо знать, это расстояние h между этими двумя точками. Здесь можно использовать тот факт, что все вершины правильного многоугольника находятся на одинаковом расстоянии от центра. Следовательно, треугольник 1-5-7 является равнобедренным прямоугольным треугольником, что позволяет легко вычислить h.
|
| 1) Графические элементы в 3D-пространстве: точки, линии, поверхности. Способы описания линий и поверхностей: неявные уравнения и параметрические функции. Неявное уравнение плоскости и прямой в пространстве.
В трехмерном пространстве различают следующие геометрические элементы:
- точки – нуль-размерные многообразия,
Объекты конечных размеров:
Для объектов конечных размеров необходимо указывать не только их положение, но и ориентацию в пространстве
Как и в двумерном случае с объектом связывают объектную систему координат, оси которой задают ориентацию объекта в пространстве
Ориентация объектной системы координат относительно мировой однозначно задается двумя углами α и β
Угол β – это угол осями OZм и OZо, называемый также углом нутации
Угол α – это угол между осями OXм и OXо, образующийся после совмещения осей OZм и OZо
…
| 4) Аффинные и перспективные преобразования в пространстве. Матрицы аффинных и перспективных преобразований
ПОВОРОТЫВ 3D-ПРОСТРАНСТВЕ:
В трехмерном пространстве аффинные преобразования описываются матрицами ранга 4, а векторы точек получают еще одну компоненту (z-компоненту)
Вращение вокруг оси абсцисс на угол j описывается матрицей:
Вращение вокруг оси ординат на угол y описывается матрицей:

Вращение вокруг оси аппликат на угол c описывается матрицей (изменение знака перед синусом по сравнению с двумя предыдущими случаями связано с требованием сохранения правовинтового характера системы координат):
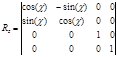
РАСТЯЖЕНИЕ/СЖАТИЕ В 3D-ПРОСТРАНСТВЕ:
Преобразование растяжения/сжатия с коэффициентами α, β и γ вдоль осей OX, OY и OZ, соответственно, описывается матрицей:
ОТРАЖЕНИЕ В 3D-ПРОСТРАНСТВЕ:
Отражение относительно плоскости XOY описывается матрицей:
Отражение относительно плоскости YOZ описывается матрицей:

Отражение относительно плоскости XOZ описывается матрицей:

|
Поиск по сайту:
|