ВВЕДЕНИЕ
Кинематикой называется раздел теоретической механики, в котором изучается движение материальных тел без рассмотрения их массы и сил, вызывающих это движение.
Движением называется изменение положения одних тел по отношению к другим телам.
Тело, по отношению к которому рассматривается движение, называется телом отсчета.
Тело отсчета и жестко связанная с ним система координат называются системой отсчета.
По виду движущихся объектов кинематика подразделяется на кинематику точки и кинематику твердого тела.
Точкой считается тело, размерами которого при изучении его движения можно пренебречь.
Движение точки, которое рассматривается относительно двух систем отсчета – подвижной и неподвижной называется сложным.
Задача кинематики твердого тела состоит в изучении движения тела в целом, а также в изучении движения каждой точки этого тела. Вид формул для определения кинематических характеристик движения тела будет зависеть от вида движения.
Основные виды движения твердого тела – поступательное, вращательное (вращение тела вокруг неподвижной оси), плоскопараллельное (плоское).
Поступательным называется такое движение твердого тела, при котором любая прямая, жестко связанная с телом, остается при его движении параллельной самой себе.
Вращательное - это такое движение тела, при котором хотя бы две его точки неподвижны.
Плоскопараллельное - это такое движение твердого тела, при котором все его точки движутся параллельно какой-нибудь неподвижной плоскости.
В настоящих методических указаниях представлены четыре задания по основным темам кинематики: К1- кинематика точки, К2-поступательное и вращательное движение твердого тела, К3 – плоское движение тела, К4- сложное движение точки.
Перед тем, как приступить к решению заданий, необходимо изучить соответствующие разделы кинематики.
З А Д А Н И Е К1
По заданным уравнениям движения точки найти уравнение траектории, скорость, ускорение, а также радиус кривизны траектории в момент времени t1. Построить график траектории, указать положение точки в момент t1 и вектора скорости и ускорения. Данные – в табл. К1.
Таблица К1
| № вар. | X=f(t) (см) | Y=f(t) (см) | t1(сек) |
| 1. | 5sin(2t) | 5cos(2t)-2 | |
| 2. | 2sin(pt/2) | 3sin(pt/2)-2 | 0,5 |
| 3. | 3t2+2t | 6t2+4t+5 | |
| 4. | 4t2+3t | 6t | |
| 5. | 2t+3 | 3t2-2t | |
| 6. | 2cos(pt/3) | 3sin(pt/3) | |
| 7. | 3sin2(pt/2) | 2cos2(pt/2) | |
| 8. | 3sin(2t) | 3cos(2t)+2 | |
| 9. | 2t2 | 1/(t+1) | |
| 10. | 3cos(pt/3)+3 | 4sin(pt/3)-2 | |
| 11. | cos2(pt/6) | sin(pt/6)-2 | |
| 12. | 2cos(pt/2) | 3cos(pt/2)-2 | 0,5 |
| 13. | 2t | 3t3-4 | |
| 14. | 2cos2(pt/4) | 3sin2(pt/4) | |
| 15. | 5t+2 | 3t2-2t+2 | |
| 16. | 5t2-2t+1 | 3t | |
| 17. | 3sin(2t) | 3cos(2t)+2 | |
| 18. | 2sin(pt/2) | 3sin(pt/2)-2 | 0,5 |
| 19. | 6t2+4t+5 | 3t2+2t | |
| 20. | 6t | 4t2+3t | |
| 21. | 3t2-2t | 2t | |
| 22. | 3sin(pt/3) | 2cos(pt/3) | |
| 23. | 3cos2(pt/2) | 2sin2(pt/2) | |
| 24. | 2cos(2t)+3 | 3sin(2t) | |
| 25. | 1/(t+1) | 2t | |
| 26. | 2cos(pt/3)-23 | 3sin(pt/3)-1 | |
| 27. | sin(pt/6) | -2cos2(pt/6) | |
| 28. | 3cos(pt/2)-2 | 2cos(pt/2) | 0,5 |
| 29. | 2t3-4 | 3t | |
| 30. | 2sin2(pt/4) | 3cos2(pt/4) |
Указания.
Для получения уравнения траектории нужно из уравнений движения исключить время. При этом, если в уравнения входят тригонометрические функции, нужно воспользоваться соотношением:  .
.
Пример выполнения задания.
Дано:
Уравнения движения точки в плоскости ху:
x = 2×t, y = t2
(х, у - в сантиметрах, t - в секундах).
Определить уравнение траектории точки; для момента времени t1 = 1 c найти скорость и ускорение точки, а также ее касательное и нормальное ускорения и радиус кривизны в соответствующей точке траектории.
Решение. Для определения уравнения траектории точки исключим из заданных уравнений движения время t. Из первого уравнения t=x/2, подставляя во второе, находим уравнение траектории точки y = x2 / 4. Таким образом траекторией будет правая ветвь параболы (поскольку значения Х и У из уравнений движения будут положительными (рис. К1.1).

Рис. К1.1
Скорость точки найдем по ее проекциям на координатные оси:


 ,
,
и при t=1 c: V1x = 2 см/c, V1y = 2 см/c, V1 = 2,83 см/c.
Аналогично найдем ускорение точки:
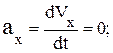

 ,
,
и при t=1 c a1x = 0 см/c2, a1y = 2 см/c2, a1 = 2 см/c2.
Касательное ускорение найдем, дифференцируя по времени равенство V2=V2x+V2y. Получим
 и
и  .
.
При t1=1 c a1t= 1,4 см/с2.
Нормальное ускорение точки  . Подставляя сюда найденные числовые значения a1 и a1t, получим, что при t1= 1 а 1n = 1,43 см/с2.
. Подставляя сюда найденные числовые значения a1 и a1t, получим, что при t1= 1 а 1n = 1,43 см/с2.
Радиус кривизны траектории r = V2/an. Подставляя сюда числовые значения V1 и a1n, найдем, что при t1=1 c r1 =5,59 см.
З а д а н и е К 2
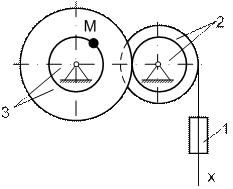
По заданному уравнению прямолинейного поступательного движения груза 1 определить скорость, а также вращательное, центростремительное и полное ускорение точки М механизма в момент времени t1. Схемы механизмов показаны на рисунке К2.1, а необходимые данные для расчета помещены в табл. К2.1.
Таблица К2.1
| Номер варианта | Радиусы, см | Уравнения движения груза 1 x=x(t) (x-в см, t в с) | t1, с | |||
| R2 | r2 | R3 | r3 | |||
| - | 10+100t2 | |||||
| - | 80t2 | |||||
| - | 18+70t2 | 1.5 | ||||
| - | 50t2 | |||||
| - | 8+40t2 | 0.5 | ||||
| - | 5+60t2 | |||||
| - | 8+40t2 | |||||
| - | 3+40t2 | |||||
| - | 3+80t2 | |||||
| - | 70t2 | 0.5 | ||||
| - | 5+40t2 | 2.5 | ||||
| - | 2+50t2 | 1.5 | ||||
| - | 60t2 | |||||
| - | 6+20t2 | |||||
| - | 7+90t2 | |||||
| - | 4+30t2 | |||||
| - | 80t2 | 0.5 | ||||
| - | 4+20t2 | 1.5 | ||||
| - | 5+80t2 | |||||
| - | 50t2 | |||||
| 4+90t2 | 0.5 | |||||
| - | 10+40t2 | |||||
| - | 2+50t2 | |||||
| 90t2 | ||||||
| 50t2 | ||||||
| 5+60t2 | ||||||
| 6+30t2 | 0.5 | |||||
| 7+40t2 | ||||||
| 3+30t2 | 1.5 | |||||
| - | 5+60t2 |
1.

| 2.

|
3.

| 4.

|
5.

| 6.

|
7.

| 8.

|
9.

| 10.

|
11.

| 12.

|
13.

| 14.

|
15.

| 16.

|
17.

| 18.

|
19.

| 20.

|
21.
| 22.

|
23.

| 24.

|
25.

| 26.

|
27.

| 28.

|
29.

| 30.

|
Рис К2.1
Указания. Для решения задачи следует изучить формулы для определения кинематических характеристик поступательного и вращательного движения тела.
Пример выполнения задания.
Дано:
Схема механизма (рис. К2.2); x = 2+70t2 см; (t - в с);R2 = 50 см; r2 = 30 см; R3 = 60 см; r3 = 40 см; t1 = 0,75 с.

Рис. К2.2
Решение. Дифференцированием по времени уравнения движения найдем скорость груза:
 см/с.
см/с.
Угловая скорость звена 2
 с-1.
с-1.
Угловые скорости колес 2 и 3, связанных гибкой передачей найдем из соотношения:

откуда
 с-1.
с-1.
Угловое ускорение
 с-2 = const.
с-2 = const.
Скорость точки М

и направлена перпендикулярно к радиусу в сторону вращения колеса 3.
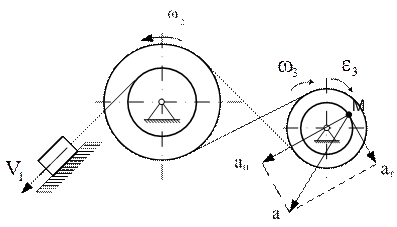
Рис К2.3
Касательное ускорение точки М

и имеет одинаковое со скоростью направление, так как в рассматриваемом примере вращение колес ускоренное.
Нормальное ускорение точки М

и направлено по радиусу к центру колеса.
Полное ускорение
 .
.
Направления векторов скорости и ускорения показаны на рис К2.3. Значения этих величин для момента времени t = t1 сведены в таблицу К2.2.
Таблица К2.2
 , с -1 , с -1
| 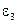 , с-2 , с-2
| V, см/с | Ускорение, см/с2 | ||
| at | an | а | |||
| 2,92 | 3,89 | 116,67 | 155,6 | 341,1 | 374,9 |
З а д а н и е К3
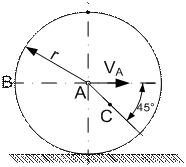
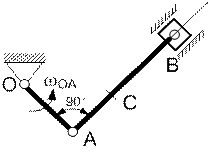
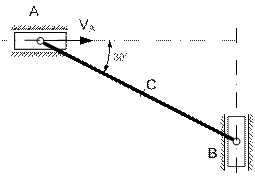
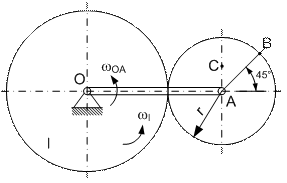
Для заданного положения механизма найти скорости точек В и С, а также угловые скорости звеньев. Схемы механизмов изображены на рис. К3.1, а необходимые данные для расчета приведены в табл. К 3.1
Таблица К3.1
| Номер варианта | Размеры, см | wOA, с-1 | wI, с-1 | VA, см/с | |||
| ОА | r | АВ | АС | ||||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | - | - | |||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | ||||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | ||||||
| - | - | - | |||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | 2.5 | - | |||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | |||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | |||||
| - | 1.2 | - | |||||
| - | - | - | - | ||||
| - | - | - | - | ||||
| - | - | - | |||||
| - | - | - | - |
Примечания. wOA - угловая скорость кривошипа ОА при –заданном положении механизма; wI - угловая скорость колеса I; VA – скорость точки А. Качение колёс происходит без скольжения.
1.

| 2.

|
3.

| 4.

|
5.

| 6.

|
7.
| 8.
|
9.

| 10.

|
11.
| 12.

|
13.

| 14.
|
15.

| 16.

|
17.

| 18.

|
19.

| 20.

|
21.

| 22.

|
23.

| 24.

|
25.

| 26.

|
27.

| 28.

|
29.

| 30.

|
Рис К3.1
Указания. Для решения задачи следует ознакомиться с методами определения скоростей точек тела, совершающего плоское движения (при помощи теоремы о проекциях скоростей или с помощью мгновенного центра скоростей).