Дано:
Схема механизма в заданном положении (рис. К3.2); исходные данные (табл. К3.2).
Таблица К3.2
| Размеры, см | wOA, с-1 | ||
| ОА | АВ | АС | |
| 1,5 |
Решение. Вычисляем скорость точки А кривошипа ОА при заданном положении механизма:
VA = w×ОА=1,5×10 = 15 см/с.
Скорость точки А перпендикулярна к кривошипу ОА. Скорость ползуна В направлена по вертикали. Мгновенный центр скоростей РАВ шатуна АВ находится в точке пересечения перпендикуляров, проведенных из точек А и В к их скоростям (рис.К3.3.).
Рис. К3.2 Рис. К3.3
Угловая скорость звена АВ:
.
Скорости точек В и С:
VВ = wАВ×ВРАВ;
VС = wАВ×СРАВ,
где
ВРАВ = АВ×sin30° = 60×0.5 = 30 см;
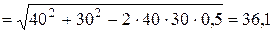см.
Следовательно,
VВ = 0,29×30 = 8,7 см/с;
VС = 0,29×36,1 = 10,5 см/с.
Вектор 
направлен перпендикулярно к отрезку СРАВ в сторону, соответствующую направлению вращения звена АВ.
З а д а н и е К 4
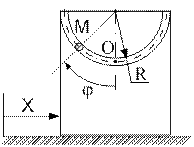
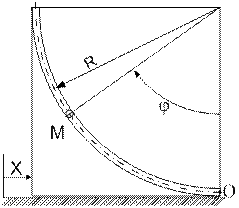
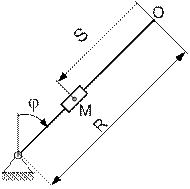
Определить абсолютную скорость и абсолютное ускорение точки М в момент времени t1. Схемы движения показаны на рисунке К4.1, данные для расчета в таблице К4.
Таблица К4
| Вар | j (t), рад | S(t), см | Х(t), см | R, см | а, см | t1, с |
| 3t | 5t2+15t | - | - | |||
| 5t | 5t2+5t | - | - | |||
| 2t | 3t | - | - | - | 0,5 | |
| 4t | 2t2+5t | - | - | |||
| 2t | 3t+5 | - | - | |||
| 2t | 4t+10 | - | - | |||
| 5t | 3t2+5 | - | - | - | 0,5 | |
| 2t | 2t2+3 | - | - | |||
| t+1 | 2pt | - | ||||
| 2t | 2pt | - | 2,5 | |||
| 3t | 2t2+6t | - | - |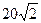 
| ||
| 2t | 2t2+8t | - | - | 
| ||
| 3t | 5t | - | - | - | ||
| 2t | 3t | - | - | - | ||
| 3t | 4t | - | - | - | ||
| 2t | 3t | - | - | |||
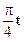
| - | 2t2 | - | |||
| - | 3t2+2t | - | |||
| - | 5t2 | 3t2+2 | - | - | 0,5 | |
| - | 3t2 | 2t2+t | - | - | ||
| - | 2t2 | 3t3-2t | - | - | ||
| - | 3t2 | 2t3+3t | - | - | ||
|
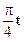
| - | 6t2+2t | - | |||
|
| - | 3t3-2t2 | - | |||
| 2t | 2t2+t | - | - | - | ||
| 3t | 3t3-2t | - | - | - | ||
|
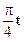
| 5t2-3t | - | - | |||
|
| 2t2+3t | - | - | |||
| 3t | 2t2+2t | - | - | - | ||
| 2t | t2+4t | - | - |
1.
| 2.
|
3.
| 4.
|
5.
| 6.
|
7.
| 8.
|
9.
| 10.
|
11.
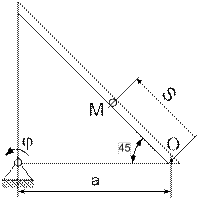
| 12.
|
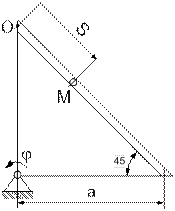
13.
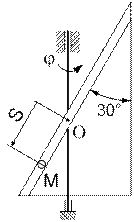
| 14.
|
15.
| 16.
|
17.
| 18.
|
19.
| 20.
|
21.
| 22.
|
23.
| 24.
|
25.
| 26.
|
27.
| 28.
|
29.
| 30.
|
Рис. К4.1
Указания. Для решения задачи следует воспользоваться формулами для определения абсолютной скорости и ускорения точки при сложном движении, при этом необходимо понять сущность понятий переносной и относительной скоростей и переносного и относительного ускорений. А также ускорения Кориолиса.
Пример выполнения задания.
Дано:
Пластина вращается по закону:j=2t (рад), по ее диагонали движется точка М согласно уравнению: 
(см) (рис.К4.2). Определить абсолютную скорость и абсолютное ускорение в момент времени t1=1 c.
Рис. К4.2
Решение. Относительным является движение точки по пластине, а переносным – вращение пластины.
Для того, чтобы найти относительную скорость нужно остановить переносное движение, то есть вращение пластины:
При t=1 с Vотн=0.
Для определения переносной скорости нужно остановить относительное движение, тогда Vпер направлена перпендикулярно пластине в сторону угловой скорости (рис. К4.3)
.
Переносная угловая скорость 
рад/с.
При t1=1с ОМ=S1=2cos(p/2)=2 см,
O1M=OM×cos45°= 
см,
см/с.
Абсолютная скорость равна геометрической сумме переносной и относительной скоростей, а модуль ее находится по формуле:
.
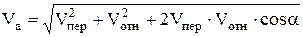Так как при t1=1c Vотн=0, то
Va=Vпер=2,82 см/с.
Рис К4.3
Абсолютное ускорение находится по теореме Кориолиса:
(1)
Относительное ускорение:
.
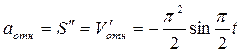При t1=1 с 
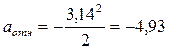см/с2 и направлено в противоположную сторону скорости.
Переносное ускорение:
.
Нормальное переносное ускорение:
см/с2.
Касательное переносное ускорение:
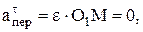
так как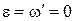 
(w=const)
Таким образом:
см/с2
и направлено к точке О1
Ускорение Кориолиса находится как удвоенное векторное произведение векторов переносной угловой скорости и относительной скорости:
.
Так как при t1=1с Vотн=0, то ак=0
Для нахождения абсолютного ускорения складываем вектора 
и 
. Для этого формулу (1) проектируем на оси координат:
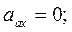
см/с2;
см/с2;
см/с2.