Другие агрегатные индексы

Рассмотрим некоторые из агрегатных индексов.

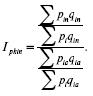
1. Индекс себестоимости продукции показывает, во сколько раз себестоимость в отчетном периоде в среднем выше или ниже базисной или плановой себестоимости, а также абсолютный размер экономии или перерасхода в результате изменения себестоимости. Индекс себестоимости – это индекс качественных показателей и исчисляется по весам (объему) продукции отчетного периода:

где z₁, – себестоимость единицы продукции в отчетном периоде;

z₀ – себестоимость единицы продукции в базисном (или плановом) периоде;

q₁ – количество продукции в отчетном периоде.

2. Индекс производительности труда. Производительность труда определяется количеством продукции, произведенной в единицу времени, или затратами рабочего времени на производство единицы продукции. Для определения изменения производительности труда в отчетном периоде по сравнению с базисным нужно затраты рабочего времени на производство единицы продукции в базисном периоде (t₀) разделить на затраты рабочего времени на производство единицы продукции в отчетном периоде

2.1 Индивидуальный индекс производительности труда равен:

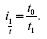
Для построения агрегатного индекса производительности труда необходимо затраты рабочего времени на производство одной единицы продукции взвесить на количество продукции, произведенной в отчетном периоде:

где t ₁ q₁ – фактические затраты времени на производство всей продукции в отчетном периоде;

2.2 Агрегатный индекс производительности труда рассчитывается по объему продукции отчетного периода.

t₀q₁ показывает, сколько времени потребовалось затратить на производство всей продукции отчетного периода в базисном периоде.

3. Индекс трудоемкости характеризует модификацию трудоемкости единицы продукции в отчетном периоде по сопоставлению с базисным. Величина индекса трудоемкости обратно пропорциональна величине индекса производительности труда, вычисленной по затратам времени на производство единицы продукции.

Формула индивидуального индекса:

а агрегатного:

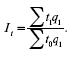
Индекс трудоемкости – это индекс качественных показателей, и рассчитывается он также по весам отчетного периода.

4. Индекс выполнения плана. При его вычислении фактические данные сопоставляются с плановыми, причем весами индекса могут быть показатели плановые и фактические.

5. Среднеарифметический и среднегармонический индексы.

Агрегатные индексы цен, физического объема товарооборота и другие могут быть рассчитаны, если известны индексируемые величины и веса, т. е. p и q.

Допустим, что имеется произведение pq и индивидуальные индексы. Возникает проблема построения средних индексов, идентичных агрегатным, путем осреднения индивидуальных индексов. Эта задача решается преобразованием агрегатного индекса в среднеарифметический и среднегармонический индексы.

Преобразование агрегатного индекса в среднеарифметический можно рассмотреть на примере агрегатного индекса физического объема товарооборота.

Если не известны отдельные значения q₀ и p₀, а дано их произведение q₀p₀ – товарооборот базисного периода и индивидуальные индексы цен . В данном случае сводный индекс рассчитывается с базовыми весами.

Из индивидуального индекса физического объема товарооборота следует, что .

Если заменить q₁ в числителе агрегатного индекса физического объема товарооборота на , то получим .

Это среднеарифметический индекс физического объема товарооборота.

Но если не известны отдельные значения q₁ и p₁, а дано их произведение q₁p₁ – товарооборот отчетного периода и индивидуальные индексы цен , и сводный индекс рассчитывается с отчетными весами, то применяется среднегармонический индекс цен.

Необходимо, чтобы индивидуальные индексы были взвешены так, чтобы среднегармонический индекс совпал с агрегатным.

Из формулы определяем неизвестное значение р₀ и, заменив в формуле агрегатного индекса цен значение 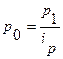получаем

Этот индекс называется среднегармоническим.

6. Индексы средних величин

Индексы переменного и фиксированного состава

Иногда при изучении динамики общественных явлений можно заметить, что ее уровни выражены средними величинами (средней себестоимостью, средней заработной платой, средней производительностью труда и т. д.). Динамика средних показателей зависит от одновременного изменения вариантов, из которых формируются средние, и изменения удельных весов этих вариантов, т. е. от структуры изучаемого явления.

На изменение динамики среднего значения изучаемого статистического процесса или явления могут оказывать влияние одновременно два фактора:

1) изменение осредняемого показателя

2) изменение структуры.

Изучение совместного действия указанных факторов на общее изменение динамики среднего уровня явления, а также роли и влияния каждого фактора в отдельности в общей динамике средней проводится в статистике при помощи системы взаимосвязанных индексов.

Различают индексы переменного и фиксированного состава. Рассмотрим их построение и содержание на примере индекса себестоимости продукции.

На величину индекса себестоимости продукции влияют изменения себестоимости единицы продукции в каждой фирме и изменения роли отдельных фирм в общем объеме выпускаемой продукции.

Общий индекс определяем как отношение следующих двух средних:

, Þ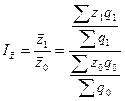

Индексы, отражающие изменение средних величин за счет влияния индексируемых величин при переменных весах, называются индексами переменного состава.

Индексы, отражающие изменение средних величин за счет влияния индексируемых величин при постоянных весах, называются индексами фиксированного (постоянного) состава.

При построении индекса фиксированного состав а в качестве весов принята структура отчетного периода, что позволяет проследить изменение средней динамики изучаемого явления только за счет изменения осредняемых значений качественного показателя.

При построении индекса структурных сдвигов в качестве соизмерителя принята величина осредняемого показателя на уровне базисного периода, что дает нам возможность изучить изменение средней динамики явления только за счет структурных сдвигов.

Разложение общих индексов на факторные дает возможность определить роль отдельных факторов в общем изменении явления в относительном и абсолютном выражении.

Для анализа динамики средних показателей систему взаимосвязанных индексов, можно представить в следующем виде:

где х₁ и х₀ – уровни осредняемого показателя соответственно в отчетном и базисном периодах;

f₁ и f₂ – веса (частоты) осредняемых показателей в отчетном и базисном периодах.

Территориальные (пространственные) индексы.

Территориальные индексы нужны для сравнения показателей в пространстве, т. е. по предприятиям, округам, городам, районам и т. д. Для того чтобы построить пространственные индексы, необходимо решить ряд методологических вопросов, которые связаны с выбором базы сравнения и весов, или уровня, на котором будут зафиксированы веса.

При двусторонних сравнениях каждая территория может быть сравниваемой и базой сравнения. Веса этих территорий имеют равные основания использоваться при расчете индекса. Однако это может привести к различным или противоречивым результатам, этого можно избежать несколькими способами.

Один способ заключается в том, что в качестве весов принимаются объемы реализованных товаров i – го вида (I = 1, 2, 3, … n) по двум регионам, вместе взятым:

Q₁= q_ia+ q_ib^.

Территориальный индекс цен в данном случае вычисляется по формуле:

Второй способ расчета территориальных индексов учитывает соотношение весов на каждой из сравниваемых территорий. При данном способе первый шаг заключается в расчете средней цены каждого товара по двум территориям, вместе взятым:

после этого вычисляется территориальный индекс: