Материально-техническое обеспечение
и дидактические средства, ТСО: дидактическая карта «Основные свойства логарифмов»
Литература Основная
1. Алимов и др. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. — М.: Просвещение, 2016.
СТРУКТУРА ЗАНЯТИЯ
1. Организационная часть 2 мин
2. Сообщение темы, цели и основных заданий 2 мин.
3. Актуализация опорных знаний и мотивация учебной
деятельности (вопросы) 2мин.
4.Вопросы лекции: 80 мин.
4.1. Определение логарифма и его свойства.
4.2. Логарифмирование выражений.
4.3. Потенцирование выражений.
5. Подведение итогов, обобщение материала. 2 мин.
6. Выдача задания для самостоятельной работы студентов 2мин.
Организационная часть
Поприветствовать студентов, отметить в журнале студентов, которые отсутствуют, проверить готовность аудитории и студентов к проведению занятия.
Сообщение темы, цели и основных заданий
Актуализация опорных знаний и мотивация учебной деятельности.
Итак, мы знаем, что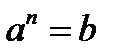 
, а если n – неизвестно? Как можно найти показатель степени из равенства: 
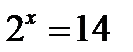? Никакие известные нам действия не помогут. Вот поэтому вводится новое понятие, понятие логарифма.
1. Проверка домашнего задания.
2. Фронтальный опрос
2.1. Определение показательной функции.
2.2. Повторить свойства степени по таблице.
Лекция.
Определение логарифма и его свойства.
Определение: Логарифмом числа называется показатель степени, в которую надо возвести основание, чтобы получить данное число: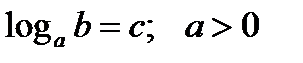 
согласно определения, имеем 
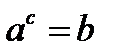, и тогда 
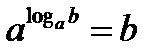– основное логарифмическое тождество.
.
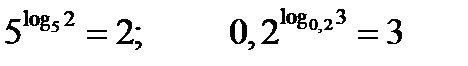Логарифмы обладают свойствами:
1.1. Логарифмы отрицательных чисел не существуют (положительное число в любой степени есть число положительное).
1.2. Логарифм единицы при любом основании равен нулю,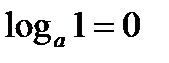 
, т.к. 
.
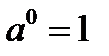1.3. Логарифм самого основания равен 1, то есть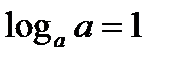 
, т.к.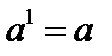 
1.4. Логарифм произведения при любом основании равен сумме логарифмов сомножителей при этом же основании.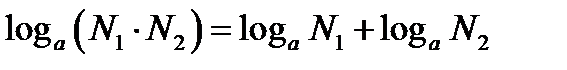 
Покажем, что это так:
Пусть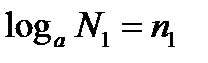 
и 
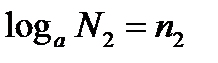; по определению логарифма имеем 
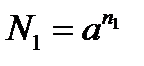и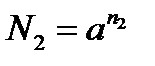 
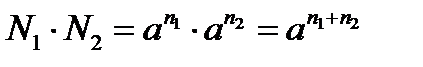; отсюда 
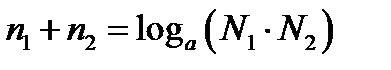и тогда 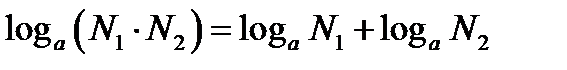, что и требовалось доказать!
1.5. Логарифм дроби при любом основании равен разности логарифма числителя и логарифма знаменателя при этом же основании
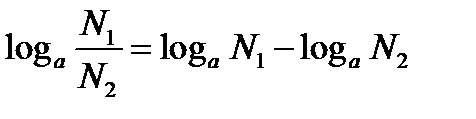
(доказательство аналогично свойству 4, докажите самостоятельно. Можно воспользоваться подсказкой учебника)
1.6. Логарифмом степени при любом основании равен произведению показателя степени на логарифм основания степени.
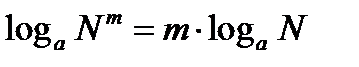
1.7. Логарифм числа с основанием 10 называется десятичным и имеет особую запись.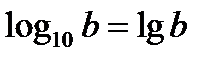 
1.8. Логарифм числа с снованием e называется натуральным и имеет также особую запись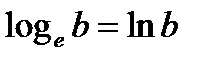 
. 
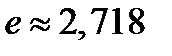число Непера (экспонента).
И десятичный, и натуральный логарифмы любого числа можно находить при помощи МК
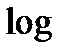17,4 
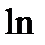0,384
А если надо вычислить логарифм числа при любом основании? Что делать? Надо перейти к основанию 10 или e.
По определению логарифма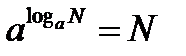 
, используя свойство логарифмов (смотрите свойство 6) имеем 
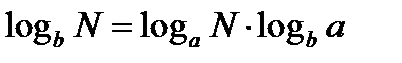и тогда 
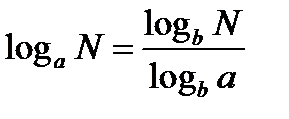и называется формулой перехода от одной системы логарифмов к другой. Эта формула часто применяется при решении логарифмических уравнений и неравенств 
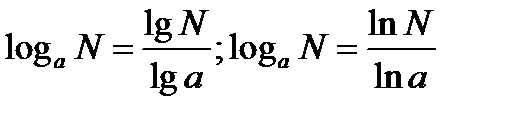, что даёт возможность вычисления выполнять при помощи МК.
Решить: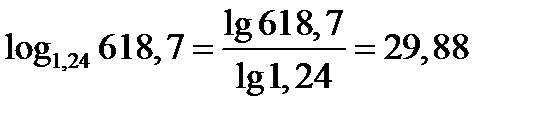 
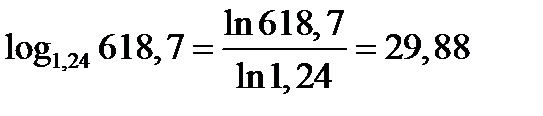
Как видно результаты равные поэтому можно делать переход к любому основанию.
Проверьте результат: 
Самостоятельно: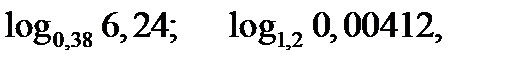 
Пособие: стр. 28 № 3.27 вместе с преподавателем; № 3.21; 3.23 – самостоятельно (с последующей проверкой)
Замечания: 1)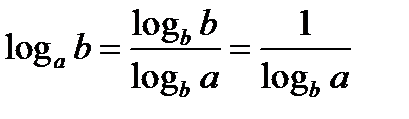 
, 2) 
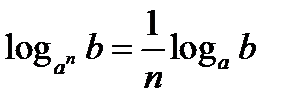3) 
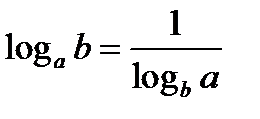
Используя определение логарифма, можно находить переменную.
Рассмотрим на конкретных примерах.
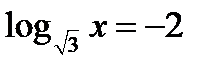по определению логарифма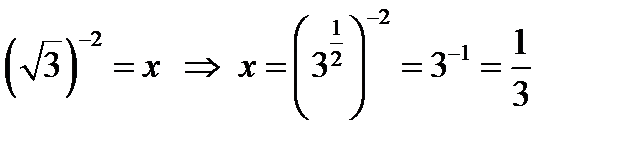 
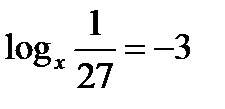по определению логарифма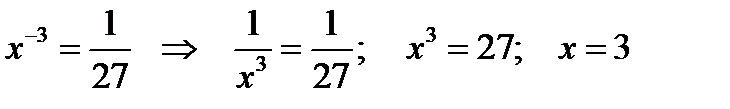 
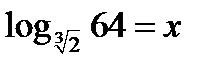по определению логарифма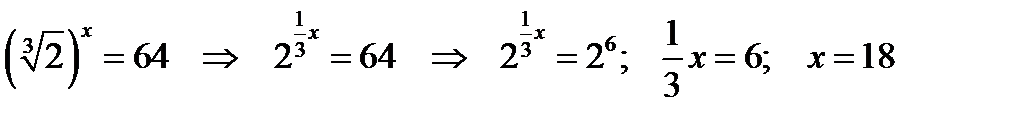 
Решить. № 3.4; 3.8; 3.9; 3.11; 3.16; 3.20
3.4.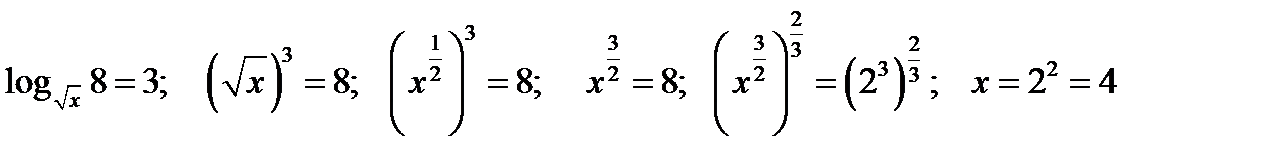 
3.8.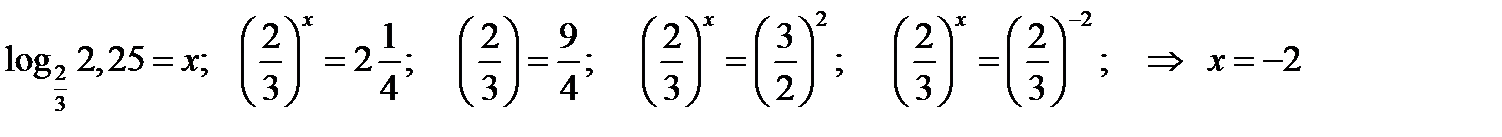 
3.9.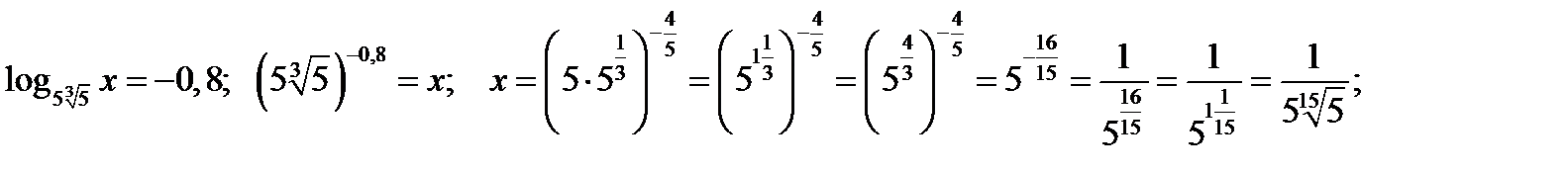 
3.11.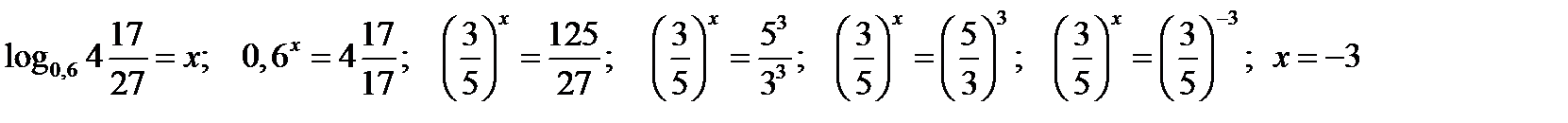 
3.16.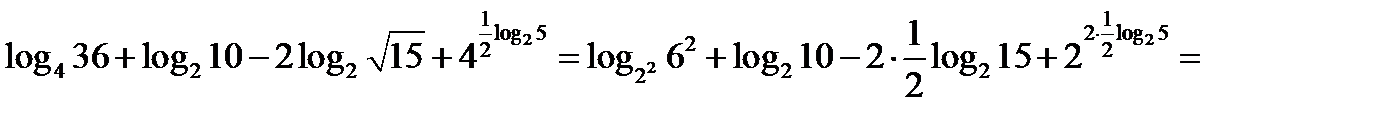 
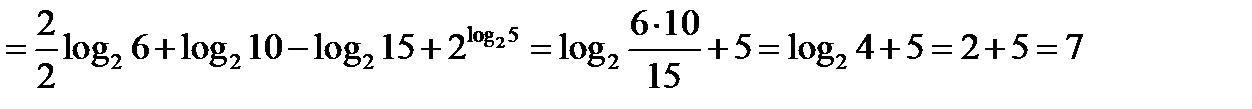
3.20.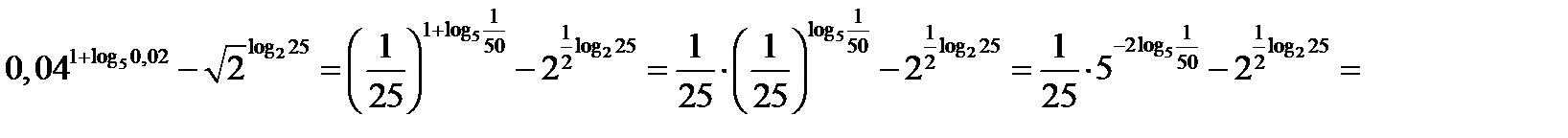 
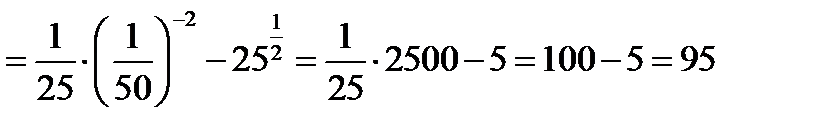
Самостоятельно:
Пособие стр. 28 № 3.22; 3.24 (МК) 3.10; 3.12; 3.13; 3.14; 3.18
3.10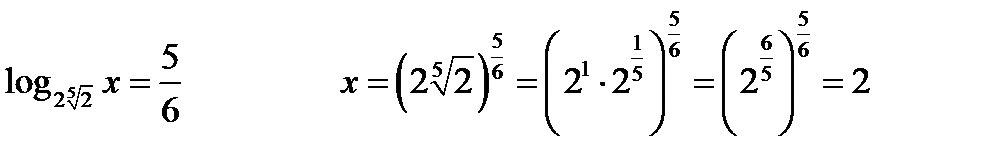 
3.12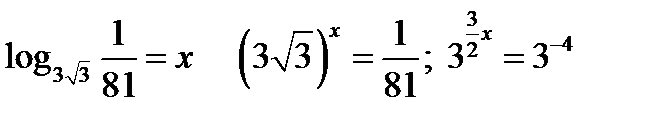 
3.14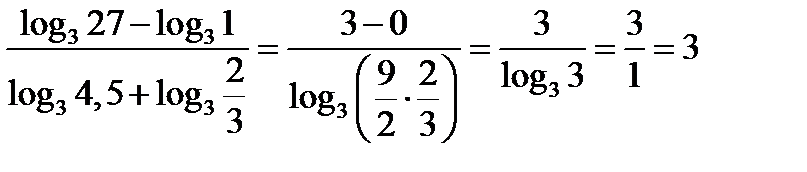 
3.18 