ПРОВЕРКА ПОЛУЧЕННОЙ МАССЫСОСТАВА НА ПРОХОЖДЕНИЕ ПОДЪЕМОВ БОЛЬШЕЙ КРУТИЗНЫ, ЧЕМ РАСЧЕТНОЙ, С УЧЕТОМ НАКОПЛЕННОЙ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
Если характер профиля пути, расположение остановочных пунктов и допускаемые скорости движения по состоянию пути на участке не позволяют надежно определить расчетный затяжной подъем, то массу состава рассчитывают методом подбора.
Масса состава проверяется на прохождение поездом участков профиля большей крутизны, чем расчетный подъем, учитывая при этом использование кинетической энергии поезда.
Проверим прохождение состава по элементу № 6.( = 9, длина 2000 м).
= 9, длина 2000 м).
Проверку выполняем путем аналитической интерпретации уравнения движения поезда с помощью выражения:

где 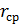 - удельная замедляющая сила на рассмотренном интервале скорости, Н/т;
- удельная замедляющая сила на рассмотренном интервале скорости, Н/т;

Все расчеты сводим в таблицу.
Таблица 3.1- Расчет движения поезда по подъему с уклоном 8‰
 км/ч
км/ч
|  км/ч
км/ч
| 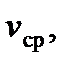 км/ч км/ч
|  Н Н
| 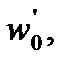 Н/т
Н/т
| 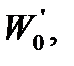 Н
Н
| 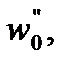 Н/т
Н/т
|  Н
Н
|  Н
Н
| 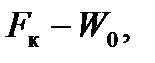 Н
Н
|  Н/т
Н/т
| 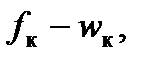 Н/т Н/т
|  м м
|
| 43,4 | 18,3 | 5,3 | -85 | 735,3 | ||||||||
| 38,2 | 16,2 | 10,8 | -79 | 685,7 | ||||||||
| 33,6 | 14,5 | 19,7 | -70 | 654,8 |
Значение  определяем из формулы (4)
определяем из формулы (4)
 H/т.
H/т.
Значение 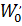 определяем по формуле:
определяем по формуле:
 (12)
(12)

Значение  определяем по формулам 6-10:
определяем по формулам 6-10:
 H/т
H/т
Значение  определяем по формуле:
определяем по формуле:
 (13)
(13)
 H.
H.
Значение 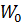 определяем по формуле:
определяем по формуле:
 (14)
(14)
 H
H 
 H;
H;


 Н/т.
Н/т.
Значение 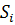 определяем из формулы 10:
определяем из формулы 10:


Исходя из результатов таблицы 3.1, видим, что  , то поезд преодолеет подъем и скорость его не опустится ниже расчетной.
, то поезд преодолеет подъем и скорость его не опустится ниже расчетной.
ПРОВЕРКА ПОЛУЧЕННОЙ МАССЫСОСТАВА НА ТРОГАНИЕ С МЕСТА НА ОСТАНОВОЧНЫХ ПУНКТАХ
Проверку выполняем по формуле:

где  – сила тяги локомотива при трогании, Н;
– сила тяги локомотива при трогании, Н;  =714000 Н;
=714000 Н;
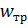 – удельное сопротивление движ. поезда при трогании, Н/т;
– удельное сопротивление движ. поезда при трогании, Н/т;
 – уклон элемента, на котором осуществляется трогание, ‰.
– уклон элемента, на котором осуществляется трогание, ‰.
Принимаем, что в составе все подшипники качения, тогда удельное сопротивление при трогании определяется по формуле:
 где
где 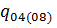 – средняя осевая нагрузка,которая рассчитывается по формулам 7 – 8.
– средняя осевая нагрузка,которая рассчитывается по формулам 7 – 8. 



Так как у нас 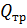 = 28504 т >
= 28504 т >  = 4300 т, то заданный локомотив сможет тронуться с места рассчитанную массу состава на всех станциях.
= 4300 т, то заданный локомотив сможет тронуться с места рассчитанную массу состава на всех станциях.
ПРОВЕРКА ПОЛУЧЕННОЙ МАССЫПО ДЛИНЫПРИЕМО-ОТПРАВОЧНЫХ ПУТЕЙ
Для проверки определим длину поезда:
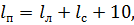 (18)
(18)
где  - длина локомотива, м;
- длина локомотива, м;  =36 м;
=36 м;
 - длина состава, м;
- длина состава, м;
 - допуск на неточность установки поезда.
- допуск на неточность установки поезда.
Длину состава определяем по формуле:

где 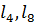 – суммарная длина 4 – и 8 – осных вагонов, которая определяется по формуле:
– суммарная длина 4 – и 8 – осных вагонов, которая определяется по формуле:

где 
 – длина 4 – и 8 – осного вагона соответственно.
– длина 4 – и 8 – осного вагона соответственно.
Длина вагонов составляет в соответствии с:
-четырехосных-14 м;
-восьмиосных-21 м.
Количество 4,8  ми осных вагонов находим по формулам:
ми осных вагонов находим по формулам:





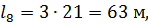


Т.к. длина приемо-отправочных путей  = 1250 м, то тогда длина поезда не превышает длины приемо-отправочных путей.
= 1250 м, то тогда длина поезда не превышает длины приемо-отправочных путей.
СПРЯМЛЕНИЕ ПРОФИЛЯ ПУТИ НА ДАННОМ УЧАСТКЕ
Продольный профиль железнодорожного пути состоит из отдельных элементов, каждый из которых характеризуется длиной и величиной уклона. В плане железнодорожный путь кроме прямолинейных включает и криволинейные участки, характеризуемые радиусом либо центральным углом и длиной кривой. Влияние продольного профиля и кривизны пути на движение поезда учитывают величиной дополнительного сопротивления движению. Поскольку при производстве тяговых расчетов поезд обычно рассматривают, как материальную точку расчет скорости движения выполняют для каждого элемента профиля в отдельности. При этом считают, что дополнительное сопротивление от уклона при переходе поезда на очередной элемент профиля пути изменяется мгновенно. На самом деле поезд, имеющий вполне определенную длину, может располагаться на нескольких элементах, как это показано на рисунке 5.1.
Рисунок – 5.1
Поэтому целесообразно в расчетах заменить несколько мало отличающихся крутизной элементов одним, длина которого S c равна сумме длин этих элементов. Такую операцию называют спрямлением профиля пути.
Уклон спрямленного элемента определяем по формуле:

где  уклон спрямленного элемента, ‰
уклон спрямленного элемента, ‰
 длина спрямляемого элемента, м;
длина спрямляемого элемента, м;
 длина спрямленного элемента, м.
длина спрямленного элемента, м.
Для количественной оценки возможности спрямления профиля вводят условие:

где  абсолютное значение разности между уклоном спрямленного участка и действительного значения уклона i-ого элемента, входящий в спрямляемый участок, ‰;
абсолютное значение разности между уклоном спрямленного участка и действительного значения уклона i-ого элемента, входящий в спрямляемый участок, ‰;
Кривые, имеющиеся на элементах спрямляемого профиля, учитываем с помощью зависимости:
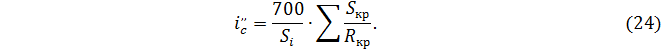
Кривые могут быть заданы длиной и центральным углом αi, задаваемым в градусах. В этом случае, выразив радиус кривой через ее длину и центральный угол, получим формулу:

Окончательный уклон спрямленного участника, на котором расположены кривые: 
Результаты расчета элементов исходного профиля занесем в таблицу 5.1.
Таблица 5.1 – Спрямление профиля участка
| № элемента | Длина, м | Уклон, ‰ | Кривые |  м м
| 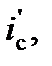 ‰ ‰
| 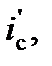 ‰ ‰
|  ‰ ‰
| 
| Номер спрямляемого элемента | Примечание | ||
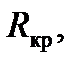 м м
|  м м
| 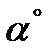
| ||||||||||
| Ст. Д | ||||||||||||
| 4,0 | - | - | - | |||||||||
| 3,0 | - | - | - | |||||||||
| - | - | - | ||||||||||
| -3,5 | - | - | - | +3,15 | 0,09 | 3,06 | ||||||
| -2,5 | - | |||||||||||
| - | - | - | +4,5 | 0,02 | 4,52 | |||||||
| 7,5 | - | |||||||||||
| 1,5 | - | - | - | 0,2 | 0,2 | 0,4 | ||||||
| - | ||||||||||||
| -10,0 | ||||||||||||
| - | +0,8 | 0,25 | 1,05 | |||||||||
| 1,5 | - | - | - | |||||||||
| 1,0 | Ст. С | |||||||||||
| -3,0 | - | +4,5 | 0,07 | 4,507 | ||||||||
| -5,0 | - | - | - | |||||||||
| - | +1,82 | 0,13 | 1,95 | |||||||||
| 4,0 | - | - | - | |||||||||
| 3,0 | - | +5,69 | 0,03 | 5,72 | ||||||||
| 6,5 | - | - | - | |||||||||
| - | - | - | +2,78 | 0,17 | 2,95 | |||||||
| 4,0 | - | |||||||||||
| -2,0 | Ст. В |
Окончание таблицы 5.1
| № элемента | Длина, м | Уклон, ‰ | Кривые |  м м
| 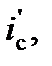 ‰ ‰
| 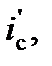 ‰ ‰
|  ‰ ‰
| 
| Номер спрямляемого элемента | Примечание | ||
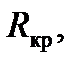 м м
|  м м
| 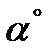
| ||||||||||
| -2,0 | - | -2,0 | 0,4 | -1,6 | - | |||||||
| -7,0 | - | -7,0 | 0,13 | -6,87 | - | |||||||
| -8,0 | - | -8,0 | 0,18 | -7,82 | - | |||||||
| - | - | - | - | - | - | |||||||
| 9,0 | 
| |||||||||||
| 7,5 | - | +7,5 | 0,095 | 7,6 | - | 
| ||||||
| 6,0 | ||||||||||||
| -1,5 | Ст.А |
Поскольку элементы 5 и 6 одного знака и мало отличаются крутизной можно попытаться их спрямить. В соответствии с выражением (22):

Проверим возможность спрямления для каждого элемента исходного профиля пути, для чего воспользуемся условием (23):

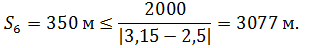
Условие для всех элементов выполнено, следовательно, спрямление возможно.
На рассматриваемом участке пути в плане расположена одна кривая. В соответствии с выражением (25) рассчитаем фиктивный подъем от этой кривой.


7. ПОСТРОЕНИЕ ДИАГРАММЫРАВНОДЕЙСТВУЮЩИХ СИЛ, ПРИЛОЖЕННЫХ К ПОЕЗДУ
При построении диаграммы удельных равнодействующих сил, приложенных к поезду, результаты расчетов сводим в таблицу 7.1. Вычисления выполняем для трех режимов движения поезда:
1) режим тяги;
2) режим холостого хода;
3) режим торможения.
Таблица 7.1 – Удельные равнодействующие силы
| Режим тяги | ||||||||
| V, км/ч | Fk, H | w0, Н/т | W0, H | w0, Н/т | W0’’, H | W0, H | Fk,- W0, H | fk-w0, Н/т |
| 8,7 | 37814,2 | 109,6 | ||||||
| 36610,6 | 39784,6 | 390215,4 | 93,2 | |||||
| 9,6 | 38734,3 | 43288,3 | 361711,7 | 86,4 | ||||
| 10,3 | 41563,5 | 48325,5 | 336674,5 | 80,4 | ||||
| 11,1 | 75,2 | |||||||
| 43,5 | 80,1 | 11056,2 | 11,5 | 46501,7 | 57557,9 | 310442,1 | 74,1 | |
| 12,2 | 49337,8 | 62999,8 | 297000,2 | 70,9 | ||||
| 13,4 | 53,6 | |||||||
| 14,8 | 59933,6 | 83807,6 | 121192,4 | 28,9 | ||||
| 16,4 | 66289,5 | 96511,5 | 56488,5 | 13,5 | ||||
| 18,1 | 73350,8 | 6251,2 | 1,5 | |||||
| 20,03 | 81117,5 | -34519,5 | -8,2 |
Окончание таблицы 7.1
| Режим холостого хода | Режим торможения | ||||||
| wx, Н/т | Wx, Н | Wx+ W0’’, H | w0x, Н/т | φкр | bт, Н/т | wox+0.5 bт, Н/т | wox+ bт, Н/т |
| 9,2 | 0,3 | 441,2 | 450,4 | ||||
| 25,45 | 3512,1 | 40122,7 | 9,6 | 0,2 | 633,6 | 326,4 | |
| 27,6 | 3808,8 | 42543,1 | 10,2 | 0,16 | 518,4 | 269,4 | 279,5 |
| 30,5 | 4202,1 | 45765,6 | 10,9 | 0,14 | 449,3 | 235,6 | 246,5 |
| 11,9 | 0,13 | 403,2 | 213,5 | 225,4 | |||
| 35,4 | 4886,3 | 12,3 | 0,12 | 390,5 | 207,5 | 219,8 | |
| 38,3 | 5278,5 | 54616,3 | 0,116 | 370,3 | 198,2 | 211,2 | |
| 43,2 | 5961,6 | 60244,6 | 14,4 | 0,11 | 345,6 | 187,2 | 201,6 |
| 48,9 | 6741,3 | 66674,9 | 15,9 | 0,10 | 326,4 | 179,1 | |
| 55,2 | 7617,6 | 73907,1 | 17,6 | 0,097 | 173,2 | 190,8 | |
| 62,3 | 8590,5 | 81941,3 | 19,6 | 0,093 | 298,5 | 168,8 | 188,4 |
| 90777,5 | 21,7 | 0,09 | 165,7 | 187,4 |
Первые два столбца таблицы заполняем тяговыми данными.
Пример заполнения таблицы приведем на основании 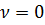 км/ч и силы тяги
км/ч и силы тяги  Н.
Н.
Далее таблицу заполняем значениями основного удельного и полного сопротивления движению локомотива при движении в режиме тяги. Удельное сопротивление для звеньевого пути определяем по формуле (4):
 H/т.
H/т.
Основное сопротивление движению локомотива вычислим по формуле (12):
 H.
H.
Основное сопротивление движению грузовых вагонов на звеньевом пути определяем по формулам (5) – (9):
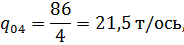



 Н/т.
Н/т.
Основное сопротивление движению состава посчитаем по формуле (13):
 H.
H.
Значение  и
и  определяем по формуле (14) и (15) соответственно:
определяем по формуле (14) и (15) соответственно:
 H,
H,
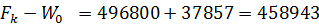 H,
H,

Для режима холостого хода удельное сопротивление определяем по формуле:
 (31)
(31)
 Н/т.
Н/т.
Полное сопротивление от локомотива определим по формуле:





Для режима торможения определим значение расчетного тормозного коэффициента: 
где 
 расчетный тормозной коэффициент;
расчетный тормозной коэффициент;

 суммарное нажатие тормозных колодок на оси.
суммарное нажатие тормозных колодок на оси.
 (35)
(35)
где 
 количество вагонов, ваг;
количество вагонов, ваг;

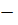 нажатие на ось, т/ось.
нажатие на ось, т/ось.
Принимаем в курсовом проекте в соответствии с ПТР
 .
.
Для грузовых поездов при спусках до 20‰ тормозные средства локомотива не учитываем, поэтому формула (34) и формула (35) примет вид:
 (36)
(36)



Расчетный коэффициент трения колодки для чугунных колодок:


Значение удельной тормозной силы определяем по формуле:
 (39)
(39)



В соответствующие столбцы записываем значения равнодействующих сил приложенных к поезду.
Диаграмма удельных равнодействующих сил, приложенных к поезду построенная в соответствии с таблицей 7.1 размещена в Приложении А.