Тема: «Построение экспериментальной математической модели биологического процесса с использованием метода наименьших квадратов»

Курсовая работа

Дисциплина: “Компьютерные технологии в медико-биологических исследованиях”

Тема: «Построение экспериментальной математической модели биологического процесса с использованием метода наименьших квадратов»

 

Вариант 12

 

 

Работу выполнил

студент гр. М6О-404Б-17

Ташов Арслан

 

Преподаватель:

Евдокименков В. Н.

 

Москва

2020

Раздел 1. Основы метода наименьших квадратов.

Постановка задачи и описание предлагаемой модели

Постановка задачи опирается на следующие предположения:

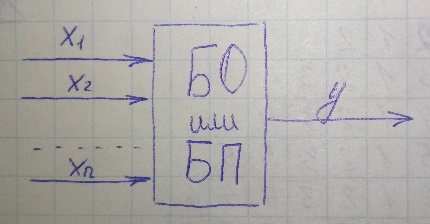
Полагаем, что состояние объекта формируется под влиянием некоторой совокупности входных воздействий x_i (i=1, …, n), называемых в дальнейшем входными переменными модели. Реакция объекта на произведенное воздействие оценивается путем измерения в ходе исследований скалярной характеристики y, называемой в дальнейшем выходной переменной модели.

Совокупность входных переменных модели в дальнейшем будем представлять в виде вектора входных переменных, компонентами которого являются входные воздействия: X = (x₁, x₂, …, x_n)^Т.

Целью является получение аналитической зависимости, описывающей связь между входными x_i, и выходной у переменными модели на основе выражения вида

y = a₁f₁(x) + a₂f₂(x) + … + a_kf_k(x)

В этом выражении а₁, а₂, …, а_k – неизвестные параметры модели, оценки которых должны быть получены на основе обработки результатов проведенных МБИ; f₁(x), f₂(x), …, f_k(x) – скалярные функции, предполагаемые заданными.

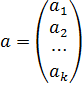– вектор размера (k × 1), компонентами которого являются неизвестные параметры моделей.

– вектор функции размера (k × 1), компоненты которого предполагаются заданными.

Тогда, с учетом введенными обозначений, искомая модель может быть описана векторным выражением вида.

y = a^T × f(x)

С целью получения оценок параметров модели а₁, а₂, …, а_k проводится серия из N экспериментов, в ходе которых на вход объекта подаются точно известные входные воздействия x^j, где j = 1, …, N – номер эксперимента, и измеряются значения y_j (j = 1, …, N), выражающие реакции объекта на эти воздействия.

Результаты проведенных экспериментов с помощью предлагаемой модели могут быть описаны следующим образом:

y₁ = a^Tf(x¹) + ε₁ = a₁f₁(x¹) + a₂f₂(x¹) +…+ a_kf_k(x¹) + ε₁

y₂ = a^Tf(x²) + ε₂ = a₁f₁(x²) + a₂f₂(x²) +…+ a_kf_k(x²) + ε₂

………………………………………………………………

y_N = a^Tf(x^N) + ε_N = a₁f₁(x^N) + a₂f₂(x^N) +…+ a_kf_k(x^N) + ε_N

Введем некоторые векторные и матричные обозначения с целью более компактного описания результатов проведенных экспериментов.

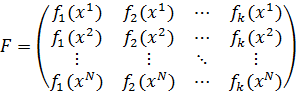
F - матрица размера (N × k), где N – количество проведенных экспериментов, а k – количество неизвестных параметров модели.

Строки этой матрицы представляют собой значения функций, присутствующих в модели, рассчитанные для того набора входных переменных, который использовался в конкретном эксперименте.

Кроме того, введем векторa

размера (N×1), компонентами которого являются измеренные в ходе экспериментов значения выходной переменной;

размера (N×1), компонентами которого являются случайные ошибки измерения выходной переменной в ходе экспериментов.

Используя введенные векторные и матричные обозначения, результаты проведенных экспериментов в компактном виде можно представить следующим образом:

Y = F ∙ a + ε

Тот факт, что в приведенном выражении присутствует случайный вектор ε, указывает на необходимость использования статистических методов для получения оценок неизвестных параметров модели. Наиболее распространенным из таких методов является метод наименьших квадратов (МНК).

Широкое использование МНК обусловлено тем, что реализация этого метода опирается на очень слабые предположения о статистических свойствах ошибок измерений, которые практически всегда выполняются в условиях реального исследования. Эти предположения сводятся к трем утверждениям:

1) Отсутствует систематическая составляющая ошибок измерения. Фактически это означает, что математическое ожидание ошибок измерений равно нулю:

М [ε_j] = 0 для ∀ j = 1,…,N

2) Ошибки ε_i, ε_j, с которыми проводится измерение выходной переменной, в разных экспериментах не коррелированы или статистически независимы:

М [ε_i­ ∙ ε_j] = 0 для ∀ i ≠ j

3) Измерения значений выходной переменной являются равноточными, т.е. дисперсия ошибок измерений во всех экспериментах одинакова:

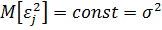для ∀ j = 1,…,N

Доказано, что оптимальным в смысле приведенного критерия является вектор оценок 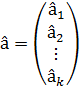параметров модели, который рассчитывается на основе выражения:

â = С∙F^TY

C – дисперсионная матрица: С = (F^T∙F)^-1 – квадратная симметричная (по способу определения) матрица размера (k×k)

Анализ точности полученной модели

В качестве характеристики точности модели используется дисперсия σ_Y² оценки значений выходной переменной с помощью модели – чем больше эта дисперсия, тем больше рассчитанное с помощью модели значение выходной переменной отличается от его истинного значения, тем более грубой является модель.

Оценим значение этой дисперсии.

σ_Y² = М[(Y-m_Y)²]

Это выражение можно записать иначе

σ_Y² = М[(Y-m_Y)^T(Y-m_Y)]

Y = â^T ∙ f(x)

m_Y = M[Y] = M[â^T ∙ f(x)] = M[â^T] ∙ f(x) = m_â^T ∙ f(x)

Y - m_Y = (â - m_â)^T ∙ f(x)

(Y - m_Y)^T = f^T(x) ∙ (â - m_â)

Тогда выражение для дисперсии σ_Y² примет вид

σ_Y² = М[f^T(x) ∙ (â-m_â) ∙ (â - m_â)^T ∙ f(x)] = f^T(x) ∙ М[(â-m_â) ∙ (â - m_â)^T] ∙ f(x)

Поскольку М[(â-m_â) ∙ (â - m_â)^T] = К_â = C ∙ σ², окончательное выражение для σ_Y²:

σ_Y² = f^T(x) ∙ C ∙ f(x) ∙ σ²

Для получения доверительных интервалов, к которым с заданной вероятностью, близкой к единице, принадлежат неизвестные нам истинные значения коэффициентов модели, используются скалярные величины вида

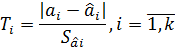
В этом выражении а_i – истинное значение параметра модели;

â_i – оценка этого параметра, полученная с помощью МНК на основе приведенного ранее выражения.

S_âi - выборочная оценка среднеквадратичного отклонения (СКО), соответствующая оценки параметра модели.

Выражение для дисперсии 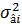, характеризующей точность оценки â_i:

,

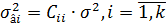где С_ii – соответствующий диагональный элемент дисперсионной матрицы С;

σ² – дисперсия ошибок измерения.

Опираясь на это выражение, выборочную оценку 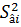дисперсии 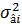можно записать так:

,

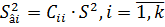где S² – выборочная оценка дисперсии ошибок измерения выходной переменной. Эта выборочная оценка рассчитывается на основе выражения:

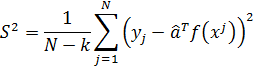
Это выражение и есть выборочная оценка дисперсий.

Тогда выборочная оценка СКО S_âi может быть получена на основе выражения:

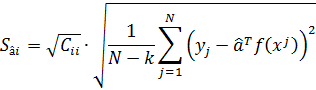
Оказывается, что определенная таким образом случайная величина T_i в ситуации, когда ошибки измерений подчиняются нормальному закону, имеет теоретическое t-распределение (распределение Стьюдента) с числом степеней свободы, равном N-k, где N – число проведенных экспериментов, k – число неизвестных параметров модели.

Допустим, что T_α – значение квантили, соответствующее доверительной вероятности α = 0,95. Тогда с вероятностью 0,95 должно выполняться неравенство

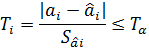
Отсюда находим границы доверительного интервала, к которому с вероятностью 0,95 принадлежат неизвестные нам истинные значения коэффициента a_i:

â_i – T_α∙S_âi­ ≤ a_i ≤ â_i + T_α∙S_âi­

Оценка адекватности полученной экспериментальной модели

Для того, чтобы иметь возможность в дальнейшем оценить адекватность полученной модели, экспериментальное исследование должно быть организовано следующим образом: для каждого конкретного набора входных переменных x^j должна быть проведена серия экспериментов i = 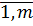(m≥2), в результате которых будет получен набор значений выходной переменной y_j¹, y_j², …, y_j^m для одного и того же набора входных переменных x^j.

Анализ адекватности модели базируется на вычислении двух оценок S₁², S₂² одной и той же дисперсии – дисперсии ошибок измерений. Причем способ вычисления оценки S₁² таков, что её величина зависит от адекватности модели. Способ вычисления оценки S₂² таков, что её величина никак не связана с адекватностью модели.

Оценка 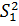рассчитывается по формуле:

Здесь

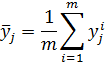
Оценка S₂² рассчитывается на основе выражения:

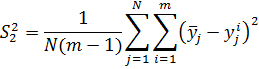
Дальнейший анализ адекватности экспериментальной модели базируется на переходе от оценок S₁², S₂² к скалярной величине F (to pay respects), которая рассчитывается на основе выражения:

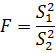
Из вида этой величины следует, что признаком адекватности модели является значение F близкое к единице. Любое нарушение адекватности модели будет сопровождаться ростом значения F. Другими словами, чем более грубой является модель, тем большее значение будет принимать величина F.

Определенная таким образом величина F обладает следующим свойством: если полученная модель является адекватной, случайная величина F имеет теоретическое F-распределение (распределение Фишера) с числом степеней свободы (N-k), (N(m-1)).

F-распределение, как и распределение Стьюдента, относится к классу теоретических распределений, связанных с нормальным. Для него в таблицах математической статистики приведены значения квантилей F_α, как правило соответствующих доверительным вероятностям α = 0.95, 0.99, 0.999.

Допустим, что F_α – значение квантили F-распределения, соответствующее вероятности 0.95. Тогда с вероятностью 0.95 можно утверждать, что предложенная модель адекватна, если имеет место неравенство

F ≤ F_α

Раздел 2. Результаты работы.

Постановка задачи.

Исследуемый процесс характеризуется набором входных переменных Х₁, Х₂, Х₃ и соответствующим им значением выходной переменной у. В процессе проведения эксперимента получены измерения выходной переменной в шести точках наблюдения. Причем, в каждой точке наблюдения при фиксированных значениях входных переменных Х₁, Х₂, Х₃ проведена серия экспериментов, в результате которых сформированы реализации выходной переменной y^ij, i = 1, …, 6; j = 1, …, 5.

Таблица экспериментальных значений:

№	X1	X2	X3	yi1	yi2	yi3	yi4	yi5
	0.5	0.6	0.4	6.17	5.26	6.46	6.09	4.43
		1.3	0.5	10.28	9.69	8.44	9.24	9.74
	1.5	1.1	2.1	9.67	10.54	9.84	11.02	9.28
		1.2	1.4	7.79	9.57	9.54	8.73	8.66
	0.5	1.4	1.2	7.97	7.66	7.64	6.67	8.52
		1.4	1.6	8.76	8.55	6.94	10.29	8.36

Цель работы: требуется на основе экспериментальных данных построить математическую модель исследуемого процесса, предполагая, что связь между выходом процесса у и значениями входных переменных может быть представлена параметрической моделью следующего вида:

y(X₁, X₂, X₃) = a^Tf(X) = a₀e^X1 + a₁X₂ + a₂X₃ + a₃,

где а₀, а₁, а₂, а₃ – неизвестные параметры модели, оценки которых должны быть получены на основе обработки экспериментального материала.

Реализация метода

Конкретизация векторных обозначений с учетом индивидуального задания:

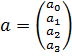– вектор неизвестных параметров модели;

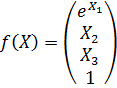– вектор функций;

Расчет вектора усредненных значений выходной переменной:

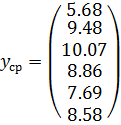
Расчет дисперсионной матрицы С = (F^TF)^-1

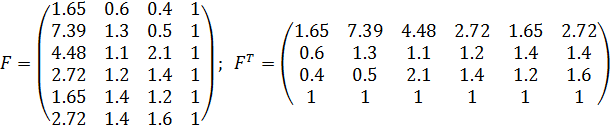
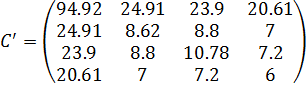
Алгебраические дополнения A_ij элементов матрицы С’:

А₁₁ = (-1)¹⁺¹М₁₁ = 4.86

А₁₂ = А₂₁ = (-1)¹⁺²М₁₂ = -13.1

А₁₃ = А₃₁ = (-1)¹⁺³М₁₃ = 4.34

А₁₄ = А₄₁ = (-1)¹⁺⁴М₁₄ = -6.62

А₂₂ = (-1)²⁺²М₂₂ = 305.61

А₂₃ = А₃₂ = (-1)²⁺³М₂₃ = -62.22

А₂₄ = А₄₂ = (-1)²⁺⁴М₂₄ = 236.87

А₃₃ = (-1)³⁺³М₃₃ = 61.13

А₃₄ = А₄₃ = (-1)³⁺⁴М₃₄ = -15.67

А₄₄ = (-1)⁴⁺⁴М₄₄ = 334.94

Определитель матрицы С’: |C’| = 102.32

Таким образом, дисперсионная матрица

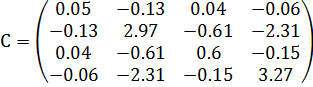
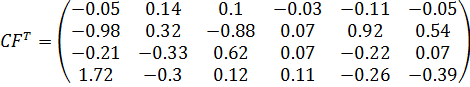
Вектор оценок параметров модели:

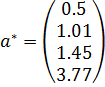
Вектор оценок значений выходной переменной в шести точках:

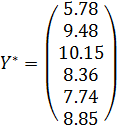
Оценка точности модели.

Значение выборочной дисперсии: S² = 0,17

Критическое значение распределения Стьюдента: Т(0,95; 2) = 4,3

Границы доверительных интервалов:

0,1 ≤ а₀ ≤ 0,9

-2,04 ≤ а₁ ≤ 4,06

0,08 ≤ а₂ ≤ 2,82

0,57 ≤ а₃ ≤ 6,97

Оценка адекватности модели.

Дисперсия ошибок модели: S₁² = 0,17

Дисперсия ошибок измерений: S₂² = 0,68

Значение статистики Фишера: F = 0,25

Критическое значение F-распределения: F(0,95; 2; 24) = 3,4

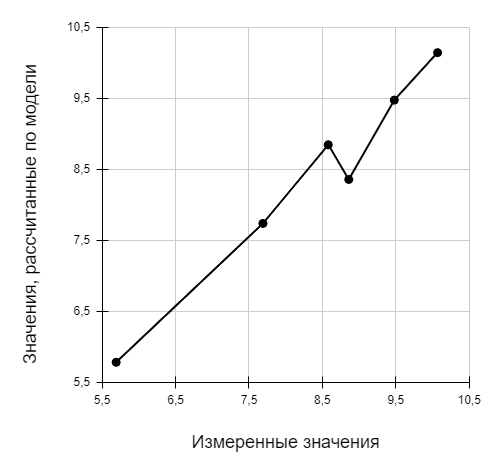
Зависимость, отражающая соотношение между значениями выходной переменной, рассчитанной по модели, и измеренными значениями.

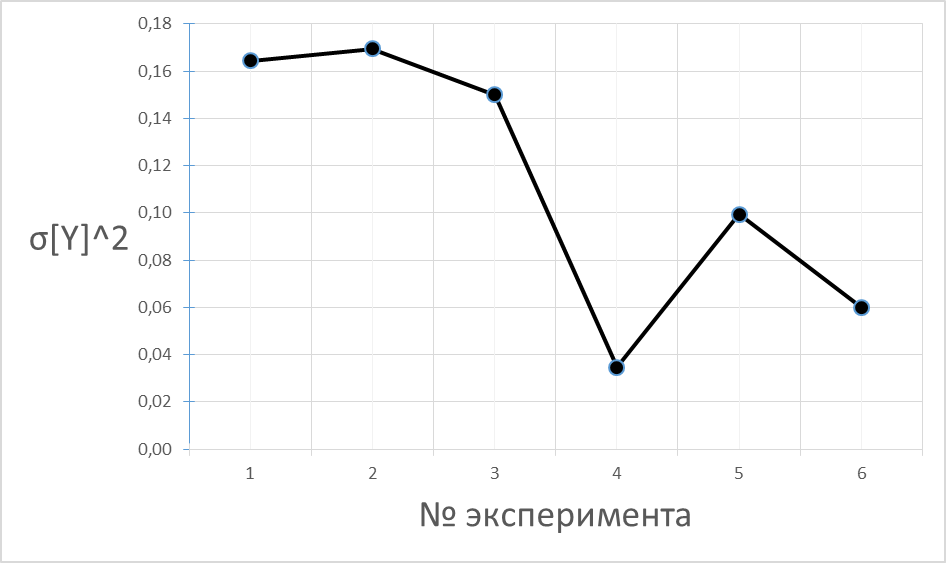
Зависимость, отражающая распределение значений дисперсий оценки выходной координаты.