Тема 1.5. Центр тяжести тела
§1. Центр тяжести однородного тела.
Рассмотрим твердое тело весом P и объемом V в системе координат Oxyz, где оси x и y связаны с поверхностью земли, а ось z направлена в зенит.
Если разбить тело на элементарные части объемом ∆ Vi, то на каждую его часть будет действовать сила притяжения ∆ Pi, направленная к центру Земли. Предположим, что размеры тела значительно меньше размеров Земли, тогда систему сил, приложенных к элементарным частям тела можно считать не сходящейся, а параллельной (рис.1), и к ней применимы все выводы предыдущей главы.
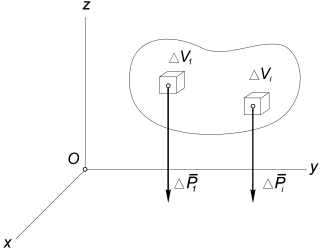 Рис.1.Параллельная система сил
Центром тяжести твердого теланазывается центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.1.Параллельная система сил
Центром тяжести твердого теланазывается центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
 Рис.2.Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.2.Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
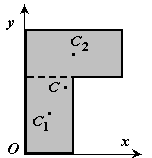 Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
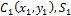 - центр тяжести и площадь первой фигуры; - центр тяжести и площадь первой фигуры;
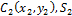 - центр тяжести и площадь второй фигуры; - центр тяжести и площадь второй фигуры;
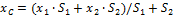 - координата центра тяжести сплошной сложной геометрической фигуры по оси x; - координата центра тяжести сплошной сложной геометрической фигуры по оси x;
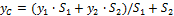 - координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей.Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 . - координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей.Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
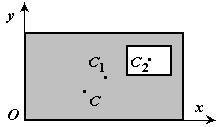 Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
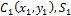 - центр тяжести и площадь первой фигуры; - центр тяжести и площадь первой фигуры;
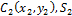 - центр тяжести и площадь второй фигуры; - центр тяжести и площадь второй фигуры;
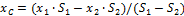 - координата центра тяжести сложной геометрической фигуры по оси x; - координата центра тяжести сложной геометрической фигуры по оси x;
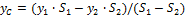 - координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3); yc =1/3(y1+y2+y3). - координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3); yc =1/3(y1+y2+y3).
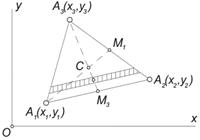 Рис.5.Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2; yc =h/2.
Рис.5.Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2; yc =h/2.
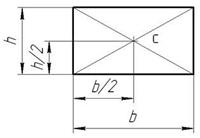 Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2; yc =4R/3π.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2; yc =4R/3π.
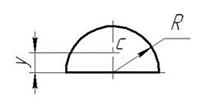 Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R; yc =R.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R; yc =R.
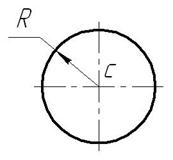 Рис. 8. Центр тяжести круга
Рис. 8. Центр тяжести круга
|
|
Поиск по сайту:
|
 Рис.1.Параллельная система сил
Центром тяжести твердого теланазывается центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
Рис.1.Параллельная система сил
Центром тяжести твердого теланазывается центр параллельных сил тяжести элементарных частей этого тела.
При определении центра тяжести полезны несколько теорем.
1) Если однородное тело имеет плоскость симметрии, то центр тяжести его находится в этой
плоскости.
2) Если однородное тело имеет ось симметрии, то центр тяжести тела находится на этой оси.
3) Если однородное тело имеет центр симметрии, то центр тяжести тела находится в этой точке.
§2. Способы определения координат центра тяжести.
1. Симметрия. Если однородное тело имеет плоскость, ось или центр симметрии (рис.2), то его центр тяжести лежит соответственно в плоскости симметрии, оси симметрии или в центре симметрии.
 Рис.2.Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
Рис.2.Центр тяжести тел, имеющих ось симметрии
2. Разбиение. Тело разбивается на конечное число частей (рис.3), для каждой из которых положение центра тяжести и площадь известны.
 Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
Рис.3. Центр тяжести сплошной
сложной геометрической фигуры
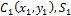 - центр тяжести и площадь первой фигуры;
- центр тяжести и площадь первой фигуры;
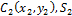 - центр тяжести и площадь второй фигуры;
- центр тяжести и площадь второй фигуры;
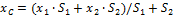 - координата центра тяжести сплошной сложной геометрической фигуры по оси x;
- координата центра тяжести сплошной сложной геометрической фигуры по оси x;
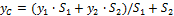 - координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей.Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
- координата центра тяжести сплошной сложной геометрической фигуры по оси y;
3. Метод отрицательных площадей.Частный случай способа разбиения (рис.4). Он применяется к телам, имеющим вырезы, если центры тяжести тела без выреза и вырезанной части известны. Тело в виде пластинки с вырезом представляют комбинацией сплошной пластинки (без выреза) с площадью S1 и площади вырезанной части S2 .
 Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
Рис.4. Центр тяжести сложной геометрической фигуры,
имеющей отверстие
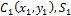 - центр тяжести и площадь первой фигуры;
- центр тяжести и площадь первой фигуры;
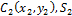 - центр тяжести и площадь второй фигуры;
- центр тяжести и площадь второй фигуры;
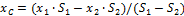 - координата центра тяжести сложной геометрической фигуры по оси x;
- координата центра тяжести сложной геометрической фигуры по оси x;
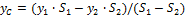 - координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3); yc =1/3(y1+y2+y3).
- координата центра тяжести сложной геометрической фигуры по оси y;
§3. Координаты центра тяжести некоторых простых фигур.
1. Центр тяжести треугольника. Центр тяжести треугольника лежит в точке пересечения его медиан (рис.5). Координаты центра тяжести треугольника представляют собой среднее арифметическое из координат его вершин: xc =1/3(x1+x2+x3); yc =1/3(y1+y2+y3).
 Рис.5.Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2; yc =h/2.
Рис.5.Центр тяжести треугольника
2. Центр тяжести прямоугольника. Центр тяжести прямоугольника лежит в точке пересечения его диагоналей (рис.6). Координаты центра тяжести прямоугольника рассчитываются по формулам: xc =b/2; yc =h/2.
 Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2; yc =4R/3π.
Рис. 6. Центр тяжести треугольника
3. Центр тяжести полукруга. Центр тяжести полукруга лежит на оси симметрии (рис.7). Координаты центра тяжести полукруга рассчитываются по формулам: xc =D/2; yc =4R/3π.
 Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R; yc =R.
Рис. 7. Центр тяжести полукруга
4. Центр тяжести круга. Центр тяжести круга лежит в центре (рис.8). Координаты центра тяжести круга рассчитываются по формулам: xc =R; yc =R.
 Рис. 8. Центр тяжести круга
Рис. 8. Центр тяжести круга