Для дальнейшего решения задачи следует вызвать мастер поиска решения, для чего необходимо выполнить операцию: Данные | Поиск решения.
После появления диалогового окна Поиск решения следует выполнить следующие действия:
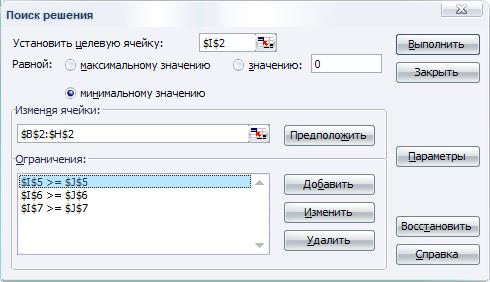
1. В поле с именем Установить целевую ячейку: ввести абсолютный адрес ячейки $I$2.
2. Для группы Равной: выбрать вариант поиска решения – минимальному значению.
3. В поле с именем Изменяя ячейки: ввести абсолютный адрес ячеек $B$2:$H$2.
4. Добавить 3 ограничения, представляющие минимальные суточные потребности в питательных веществах. С этой целью выполнить следующие действия:
§ для задания первого ограничения в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить (рис. 6.5, а);
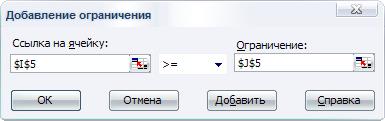
§ в появившемся дополнительном окне выбрать ячейку $I$5, которая должна отобразиться в поле с именем Ссылка на ячейку;
§ в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство "  ";
";
§ в качестве значения правой части ограничения выбрать ячейку $J$5;
§ для добавления первого ограничения в дополнительном окне нажать кнопку с надписью Добавить;
§ аналогичным образом задать оставшиеся два ограничения (рис. 6.5, б).
Добавить ограничение на допустимые значения переменных. С этой целью выполнить следующие действия:
§ в исходном диалоговом окне Поиск решения нажать кнопку с надписью Добавить;
§ в появившемся дополнительном окне выбрать диапазон ячеек $В$2:$Н$2, который должен отобразиться в поле с именем Ссылка на ячейку;
§ в качестве знака ограничения из выпадающего списка выбрать нестрогое неравенство "  ";
";
§ в качестве значения правой части ограничения в поле с именем Ограничение: ввести значение 0;
§ для добавления ограничения в дополнительном окне нажать кнопку с надписью Добавить (рис. 6.6, а).
 а
а

 б
б
Рисунок 6.5 – Параметры мастера поиска решения и базовые ограничения для задачи об оптимальной диете
 а
а
 б
б
Рисунок 6.6 – Ограничения на значения переменных и параметры мастера поиска решения для задачи об оптимальной диете
Этап. Параметры
В окне " Поиск решения " нажать клавишу " Параметры ", выбрать по " Поиск решения Линейных задач симплекс-методом ", нажать ОК, затем нажать Найти Решение (рис. 6.6, б).
После задания ограничений и целевой функции можно приступить к поиску численного решения, для чего следует нажать кнопку Выполнить. После выполнения расчетов программой MS Excel будет получено количественное решение, которое имеет вид, представленный на рис. 6.7.
Результатом решения задачи об оптимальной диете являются найденные оптимальные значения переменных: x1 = 0, x2 = 0,211, x3 = 0,109, x4= 1,887, x5 = 0, х6 = 0, x7 = 0, которым соответствует значение целевой функции: fопт= 2587,140. При выполнении расчетов для ячеек В2:I2 был выбран числовой формат с 3 знаками после запятой.
Анализ найденного решения показывает, что для удовлетворения суточной потребности в питательных веществах (белки, жиры, углеводы) следует использовать 211 г мяса баранины, 109 г сыра и 1887 г бананов, совсем отказавшись от хлеба, огурцов, помидоров и винограда. При этом общая калорийность найденной оптимальной диеты будетприближенно равна 2590 ккал, что вполне соответствует малоактивному образу жизни без серьезных физических нагрузок. Напомним, что согласно медицинским данным, энергетические затраты работников интеллектуального труда (юристы, бухгалтера, врачи, педагоги) лежат в пределах 3000 ккал.

Рисунок 6.7 – Результат количественного решения задачи
об оптимальной диете
Контрольные вопросы
1. Сформулировать основную задачу линейного программирования. Записать математическую модель ЗЛП.
2. Для чего предназначена надстройка Поиск решения?
3. Что понимают под целевой ячейкой, изменяемыми ячейками?
4. Основные этапы решения ЗЛП с помощью процессора Excel.
5. Как сохранить установочные параметры для поиска решения в виде модели?
6. Какие существуют виды отчетов и как их создать? Продемонстрировать на примере.