Модуль упругости бетона
Модуль упругости бетона
При расчетах бетонных и железобетонных конструкций по второй группе предельных состояний, в частности при определении прогибов, необходимо знать модуль упругости E (модуль Юнга) бетона при сжатии. При этом следует различать начальный Eb и приведенный Eb1 модули упругости.
Факторы, влияющие на значение расчетного модуля упругости
Более подробно сущность модуля упругости. предела пропорциональности, предела прочности, нормальных напряжений. деформаций и других понятий рассматривается отдельно. Здесь лишь отметим, что для материалов, у которых предел пропорциональности незначительно меньше предела текучести, можно использовать линейную деформационную модель. Т.е. предполагать деформации прямо пропорциональными нормальным напряжениям. Примером таких материалов являются стали различных марок. А вот бетон к таким материалам не относится. Более того, у бетона нет ярко выраженного предела пропорциональности и предела текучести. Диаграмма напряжений бетона при постепенном загружении выглядит приблизительно так:

Однако это далеко не единственная из возможных диаграмм напряжений бетона, так как на значение деформаций? будут влиять не только нормальные напряжения?. возникающие в поперечных сечениях, но и множество других факторов:
Класс бетона
Начальный модуль упругости бетона зависит от класса бетона. Значение начального модуля упругости можно определить по следующей таблице:
Таблица 1. Начальные модули упругости бетона (согласно СП 52-101-2003)

Время приложения нагрузки
При кратковременном действии нагрузки деформации бетона почти прямо пропорциональны напряжениям, кроме того такие деформации остаются упругими. При расчетах на кратковременное действие нагрузки (до 1-2 часов) значение приведенного модуля упругости на участках без трещин определяется по формуле:
где ?b1 = 0.85 - для тяжелых, мелкозернистых и легких бетонов на плотном мелком заполнителе; = 0.7 - для поризованных и легких бетонов на пористом мелком заполнителе.
При длительном действии нагрузки того же значения, деформации начинают увеличиваться до некоторого предела, например при? = Rb - до точки 1 на диаграмме напряжений. После снятия нагрузки пластические деформации ?пл останутся (потому они пластическими и называются), а при повторном загружении до указанного предела деформации будут прямо пропорциональны напряжениям. Процесс нарастания пластических деформаций с течением времени при постоянных нормальных напряжениях называется ползучестью бетона.
Так как при длительном действии нагрузки диаграмма напряжений стремится к показанной на рисунке 324.1, то при расчетах необходимо учитывать нелинейность изменения деформаций при линейно изменяющихся напряжениях. К тому же в изгибаемых элементах нелинейному изменению деформаций препятствует сам материал. Напомню, нормальные напряжения в поперечных сечениях изгибаемых элементов прямо пропорциональны расстоянию от центра тяжести сечения, через который проходит нейтральная линия, до рассматриваемой точки. Таким образом различные слои бетона, работающие совместно, приводят к частичному перераспределению деформаций по высоте элемента, при этом перераспределенную эпюру деформаций можно условно рассматривать как линейную:

На рисунке 324.2 показана некоторая высота сжатой зоны сечения у. при которой нормальные напряжения? будут прямо пропорциональны расстоянию от центра тяжести до рассматриваемой точки, это соответствует работе бетона в области условно упругих деформаций. При этом изменение деформаций можно рассматривать по зависимости, показанной на рисунке 324.2.а) или 324.2.б). Часто расчетами на прочность допускается наличие в сжатой области пластического шарнира, при котором изменяется эпюра напряжений и соответственно увеличивается значение деформаций:
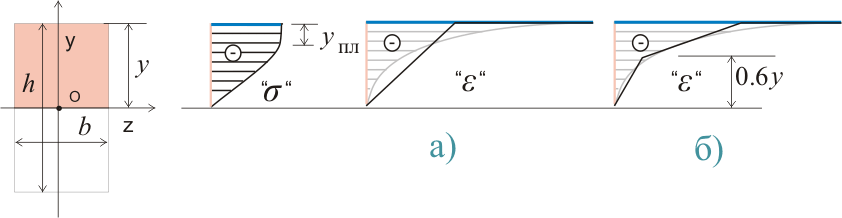
На основании этого для упрощения расчетов обычно принимается двухлинейная (рис. 324.3. а) или трехлинейная (рис. 324.3.б) диаграмма состояния сжатого бетона. Согласно СП 52.101.2003 трехлинейная диаграмма выглядит так:

Еb1 - при кратковременном действии нагрузки принимается равным Eb. а при длительном действии нагрузки определяется по следующей формуле:
где?b,cr - коэффициент ползучести бетона, определяемый в зависимости от класса бетона и влажности окружающей среды. Таким образом учитывается третий фактор, влияющий на модуль упругости бетона:
Влажность воздуха
Значение коэффициента ползучести определяется по следующей таблице:
Таблица 2. Коэффициенты ползучести бетона

а значения деформаций ?bo и ?b2 при необходимости (если нормальные напряжения больше 0.6Rb,n) определяются по таблице 3:
Таблица 3. Относительные деформации бетона (согласно СП 52-101.2003)
