Перпендикулярность плоскостей – признак и условие перпендикулярности.

Перпендикулярные плоскости, условие перпендикулярности плоскостей.

Эта статья о перпендикулярных плоскостях. Сначала дано определение перпендикулярных плоскостей, показаны обозначения и приведены примеры. После этого сформулирован признак перпендикулярности плоскостей и условие перпендикулярности двух плоскостей. В заключении детально разобраны решения характерных задач.

Навигация по странице.

• Перпендикулярные плоскости – основные сведения.
• Перпендикулярность плоскостей – признак и условие перпендикулярности.

Перпендикулярные плоскости – основные сведения.

Определение перпендикулярных плоскостей дается через угол между пересекающимися плоскостями.

Определение.

Две пересекающиеся плоскости называются перпендикулярными, если угол между ними равен девяноста градусам.

Для обозначения перпендикулярности используют символ вида « ». То есть, если плоскости и перпендикулярны, то можно кратко записать .

Если плоскости и перпендикулярны, то можно также сказать, что плоскость перпендикулярна к плоскости или плоскость перпендикулярна к плоскости . Поэтому перпендикулярные плоскости и часто называют взаимно перпендикулярными.

В качестве примера перпендикулярных плоскостей можно привести плоскости стены и пола в комнате.

К началу страницы

Перпендикулярность плоскостей – признак и условие перпендикулярности.

На практике часто приходится определять, перпендикулярны ли две заданные плоскости. Для этого можно найти угол между заданными плоскостями, и если он будет равен , то по определению плоскости будут перпендикулярными.

Также существует признак перпендикулярности двух плоскостей, который часто используется для доказательства перпендикулярности двух плоскостей. В его формулировке участвуют перпендикулярные прямая и плоскость. Сформулируем признак перпендикулярности двух плоскостей в виде теоремы.

Теорема.

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то заданные плоскости перпендикулярны.

Доказательство признака перпендикулярности двух плоскостей Вы можете посмотреть в учебнике по геометрии за 10 - 11 классы.

Из этого признака напрямую следует, что если плоскость перпендикулярна к линии пересечения двух заданных плоскостей, то она перпендикулярна к каждой из этих плоскостей.

Теперь рассмотрим необходимое и достаточное условие перпендикулярности двух плоскостей, которое удобно применять для проверки перпендикулярности плоскостей, заданных в прямоугольной системе координат в трехмерном пространстве. Определение нормального вектора плоскости позволяет доказать следующее необходимое и достаточное условие перпендикулярности двух плоскостей.

Теорема.

Для перпендикулярности двух пересекающихся плоскостей необходимо и достаточно, чтобы нормальные векторы этих плоскостей были перпендикулярны.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат. Если и - нормальные векторы плоскостей и соответственно, то необходимое и достаточное условие перпендикулярности векторов и имеет вид . Таким образом, если и - нормальные векторы плоскостей и соответственно, то для перпендикулярности плоскостей и необходимо и достаточно, чтобы скалярное произведение векторов и равнялось нулю, то есть, чтобы выполнялось равенство .

Разберем решения нескольких примеров.

Пример.

Перпендикулярны ли плоскости, заданные в прямоугольной системе координат Oxyz в трехмерном пространстве уравнениями и ?

Решение.

Чтобы ответить на вопрос о перпендикулярности заданных плоскостей, найдем координаты нормальных векторов этих плоскостей и проверим выполнение условия перпендикулярности этих векторв.

Общее уравнение плоскости позволяет сразу записать координаты нормального вектора: .

Чтобы определить координаты нормального вектора плоскости , перейдем от уравнения плоскости в отрезках к общему уравнению плоскости: . Таким образом, - нормальный вектор плоскости .

Вычислим скалярное произведение векторов и : . Так как оно отлично от нуля, то векторы и не перпендикулярны, следовательно, заданные плоскости не перпендикулярны.

Ответ:

нет, плоскости не перпендикулярны.

Пример.

В прямоугольной системе координат Oxyz в трехмерном пространстве заданы координаты четырех точек 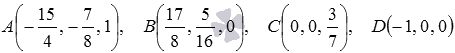. Проверьте перпендикулярность плоскостей АВС и ABD.

Решение.

Убедимся, что скалярное произведение нормальных векторов указанных плоскостей равно нулю – это будет доказательством перпендикулярности плоскостей. Для этого сначала нам нужно найти координаты нормальных векторов и плоскостей АВС и ABD соответственно.

По известным координатам точек А, В, С и D мы можем вычислить координаты векторов , и 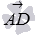(при необходимости смотрите статью вычисление координат вектора по координатам точек его конца и начала): .

Нормальным вектором плоскости АВС является векторное произведение векторов и , а нормальным вектором плоскости ABD является векторное произведение векторов и 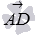, то есть,

Находим скалярное произведение векторов и : 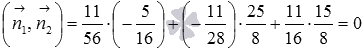. Оно равно нулю, что указывает на перпендикулярность нормальных векторов плоскостей АВС и ABD. Значит, плоскости АВС и ABD также перпендикулярны.

Заметим, что можно было по координатам заданных точек получить общие уравнения плоскостей АВС и ABD (смотрите статью уравнение плоскости, проходящей через три заданные точки), из них найти координаты нормальных векторов этих плоскостей, после чего проверить выполнение условия перпендикулярности нормальных векторов плоскостей.