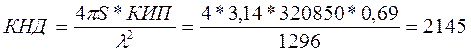Эффективная площадь антенны будет равна:
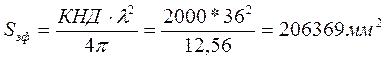
Найдем общую площадь антенны:
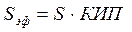
где КИП, это коэффициент использования поверхности (КИП=0.65). Следовательно, получаем что:
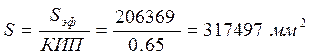
Для реализации ΔΘЕ=2 выберем Lx=930мм.
Тогда Ly=345мм.
В плоскости вектора Н выберем угол засветки φ=640
Найдем фокус антенны:
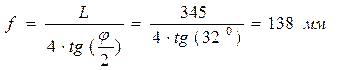
В декартовой системе координат параболоид вращения определяется уравнением (начало координат совпадает с вершиной параболоида) x2=4fz
Найдем глубину зеркала:
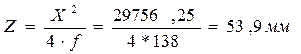
где X=L/2, а Z есть расстояние от края зеркала до облучателя.
Расстояние от облучателя до раскрыва антенны:
 |
 |
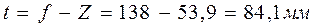
Рис. 5 Геометрические размеры антенны.
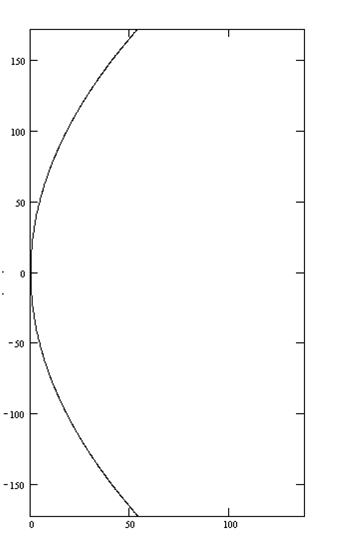
Рис. 6 раскрыв зеркала в плоскости Н.
Расчет амплитудного распределения (АР) в раскрыве зеркала
Для полученных размеров антенны и ДН облучателя рассчитываем в программе Mathcad по следующей формуле: g(θ)=Fобл(θ)cos2(θ/2).
Чтобы представить АР как функцию координаты плоского раскрыва, воспользуемся уравнением параболы x=2f tg(θ/2), откуда θ=arctg(x/2f). И пронормируем по радиусу.
Для полученного АР произведем аппроксимацию по стандартным функциям, приведенным в методичке. При этом можно определить апертурный КИП, которые представляет собой линейную комбинацию парциальных КИП (КИП i) со своими весами (Δ i)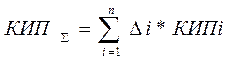 
Как было сказано раннее, ДН облучателя в плоскости вектора Н имеет следующий вид: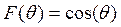 
, поэтому АР в этой плоскости определяется по формуле g(θ)= cos(θ)cos2(θ/2), и представлено на рисунке 7.
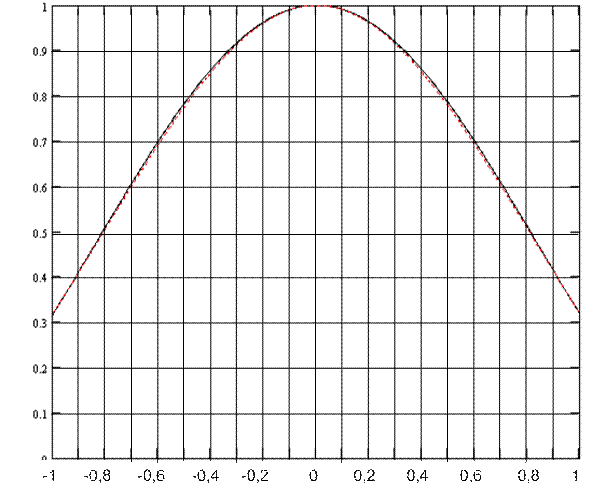
Рис. 7 АР в плоскости вектора Н (черное) и его аппроксимация (красное).
Аппроксимирующая функция имеет следующий вид:
|
|
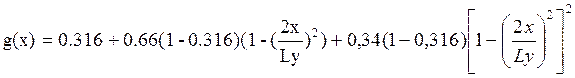
| R/Rmax | АР | Аппроксимация АР |
| 0,07 | 0,9958 | 0,9952 |
| 0,14 | 0,9836 | 0,9827 |
| 0,21 | 0,9632 | 0,9612 |
| 0,28 | 0,9355 | 0,9322 |
| 0,35 | 0,8995 | 0,8959 |
| 0,42 | 0,8587 | 0,852 |
| 0,49 | 0,8115 | 0,8029 |
| 0,56 | 0,7583 | 0,7506 |
| 0,63 | 0,7017 | 0,6939 |
| 0,7 | 0,6416 | 0,6344 |
| 0,77 | 0,5781 | 0,5726 |
| 0,84 | 0,5120 | 0,5079 |
| 0,91 | 0,4483 | 0,4461 |
| 0,98 | 0,3839 | 0,3827 |
| 0,3169 | 0,317 |
КИП=0,316*1+0,684*(0,66*0,833+0,34*0,667)=0,85
Как уже было сказано выше, АР для плоскости вектора Е будет равномерным.
Поэтому КИП=1
Среднее значение: КИП=0,92
Расчет ДН без учета тени.
ДН является линейной комбинацией соответствующих парциальных ДН (Fi) с теми же весами, умноженными на параметр амплитудного распределения (Mi),
.
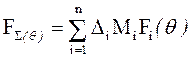Для плоскости вектора Н:
Ly=345мм
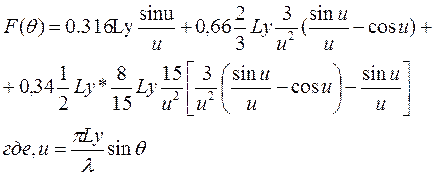
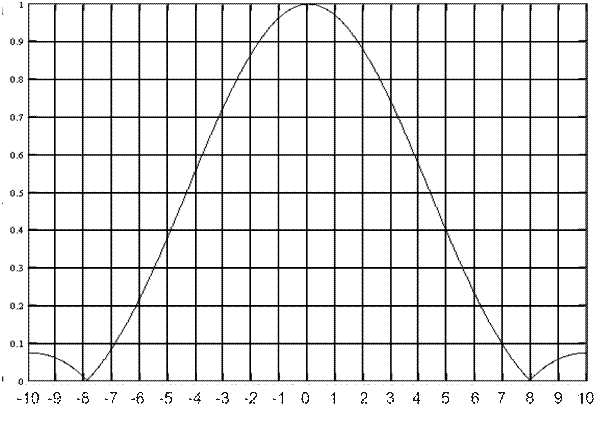
Рис. 8 ДН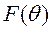 
в плоскости Н.
| Θ | F(Θ) | F(Θ) с тенью |
| 0,962 | 0,955 | |
| 0,870 | 0,854 | |
| 0,722 | 0,696 | |
| 0,560 | 0,497 | |
| 0,390 | 0,292 | |
| 0,226 | 0,102 | |
| 0,089 | 0,053 | |
| 0,001 | 0,154 | |
| 0,057 | 0,093 | |
| 0,077 | 0,073 |
Ширина ДН по уровню 0,707 ΔΘH=6,3
Для плоскости вектора Е:
Т.к. в данной плоскости равномерное распределение, то ДН будет иметь вид:
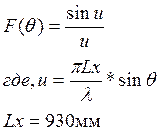
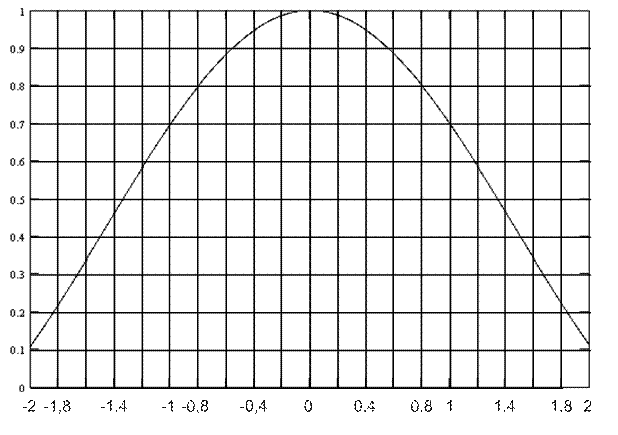
Рис. 9 ДН 
в плоскости Е.
| Θ | Fe(Θ) |
| 0,2 | 0,985 |
| 0,4 | 0,947 |
| 0,6 | 0,884 |
| 0,8 | 0,8014 |
| 0,696 | |
| 1,2 | 0,572 |
| 1,4 | 0,460 |
| 1,6 | 0,337 |
| 1,8 | 0,219 |
| 0,108 |
Ширина ДН по уровню 0,707 ΔΘЕ=1,97
Расчет ДН с учетом тени.
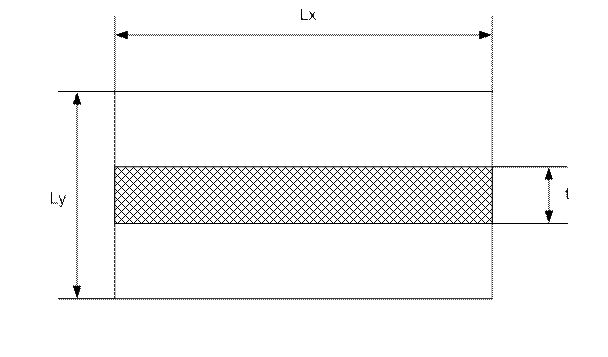
Рис. 10 Тень зеркала.
Итоговое амплитудное распределение представляется в виде суперпозиции двух амплитудных распределений: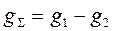 
.
Для прямоугольных раскрывов с разделяющимся по координатам АР g(X,Y)=g(X)g(Y) параметр М определяется тоже как произведение М = Мx*Мy, а параметры МX и MY имеют размерность длины. Обозначая размеры раскрыва и тени вдоль соответствующих осей через Lx, Ly и tx, ty и придавая параметру М, соответствующему тени, верхний индекс "Т", запишем ДН для плоскости XOZ
|
|
,
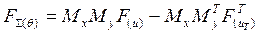где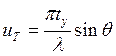 
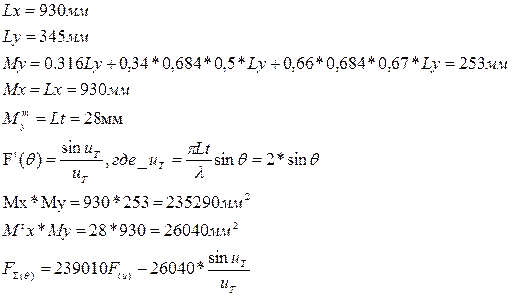
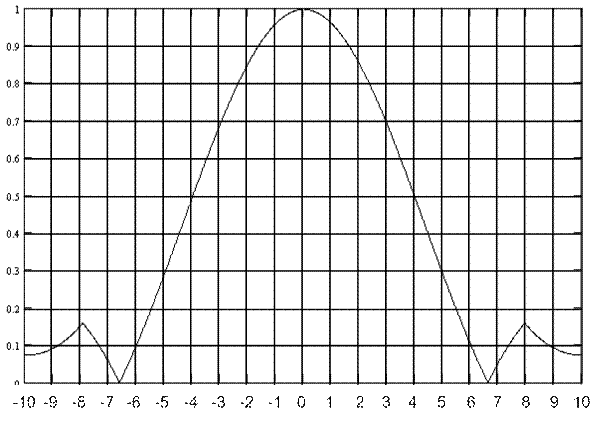Рис. 11 ДН 
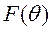в плоскости Н с учётом тени.
Ширина ДН по уровню 0,707 ΔΘН=5,7.
Расчет КИП антенны.
Полный КИП параболической антенны состоит из нескольких сомножителей: КИП=КИПА* КИПР*КИПТ,
Где КИПА-КИП раскрыва апертуры.
КИПР- КИП рассеяния.
КИПТ-КИП тени.
КИПА=0.92
КИП рассеянья:
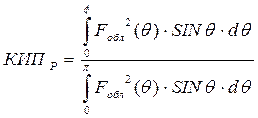
Для плоскости вектора Е: КИПР=0.9
Для плоскости вектора Н: КИПР=1
Среднее значение: КИПР=0.95
КИП тени.
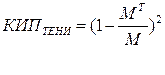
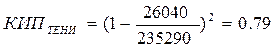
Следовательно:
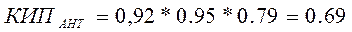
Для полученного значения КИП и площади антенны рассчитываем КНД:
