Спектральная плотность выходного сигнала находится как произведение спектральной плотности входного сигнала на ОПФ цепи.
В нашем случае:

Спектральная плотность амплитуд выходного сигнала находится как произведение спектральной плотности амплитуд на АЧХ всей цепи.
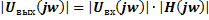
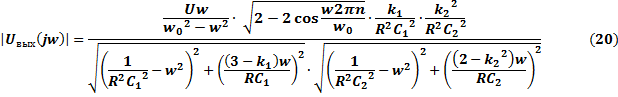
Спектральная плотность фаз выходного сигнала находится как сумма спектральной плотности фаз входного сигнала и ФЧХ всей цепи.

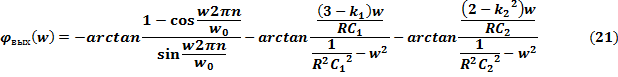
Все коэффициенты и значения берутся из рассчитанных выше пунктов.

Рис. 1.9 График спектральной плотности амплитуд выходного сигнала

Рис. 1.10 График спектральной плотности фаз выходного сигнала
6. Найдём реакцию цепи при подаче на её вход последовательности прямоугольных видеоимпульсов напряжения (см. рис. 1.1, б). Пусть период следования импульсов равен T 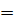 0,1(M + N)π
0,1(M + N)π 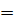 0,1(3+2)π
0,1(3+2)π 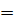 0,5π мс, а скважность Q
0,5π мс, а скважность Q 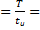 3. При таком значении скважности в ряду Фурье для воздействия будут отсутствовать третья и шестая гармоники (см. табл. 1.3). Частота первой гармоники равна
3. При таком значении скважности в ряду Фурье для воздействия будут отсутствовать третья и шестая гармоники (см. табл. 1.3). Частота первой гармоники равна  4∙
4∙ 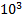
 . Тогда напряжение на входе цепи запишется с учётом данных табл. 1.3 в следующем виде:
. Тогда напряжение на входе цепи запишется с учётом данных табл. 1.3 в следующем виде:

u 1(t) 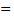 0,333
0,333 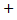 0,551∙ cos (4∙103 t –60°)
0,551∙ cos (4∙103 t –60°) 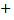 0,276∙ cos (8∙103 t –120°)
0,276∙ cos (8∙103 t –120°) 
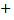 0,138∙ cos (16∙103 t –60°)
0,138∙ cos (16∙103 t –60°) 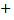 0,110∙ cos (20∙103 t –120°), В.
0,110∙ cos (20∙103 t –120°), В.
Реакция цепи u 2(t) на периодическое воздействие u 1(t) есть сумма реакций на гармонические составляющие этого воздействия:
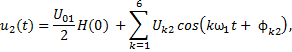
Uk2 = Uk1 ∙| H (jk ω1)|; 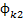 =
=  + ϴ(k ω1).
+ ϴ(k ω1).
Выражения для АЧХ и ФЧХ получены ранее:
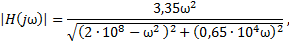
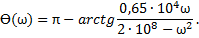
Вычислим значения АЧХ и ФЧХ на частотах гармоник входного напряжения.
При  : | H (j ω)|
: | H (j ω)| 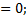 ϴ(ω)
ϴ(ω) 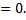
При ω 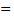 ω1
ω1 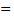 4 ∙103,
4 ∙103, 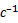 :
:


При ω 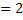 ω1
ω1  ∙103,
∙103, 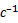 :
:
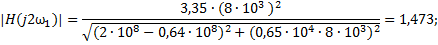

При ω  ω1
ω1 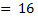 ∙103,
∙103, 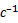 :
:
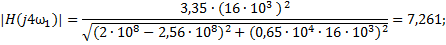

При ω  ω1
ω1  ∙103,
∙103, 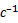 :
:
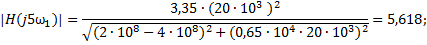
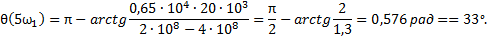
Примечание. При вычислении значений ФЧХ для четвёртой и пятой гармоник использовалась формула:
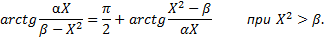
На выходе ARC -цепи амплитуда k -й гармоники изменяется в |H(jk 𝜔1)| раз, а начальная фаза – на величину ϴ(k ω1). Тогда напряжение на выходе ARC -цепи равно:
u 2(t) 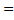 0,333∙0
0,333∙0 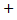 0,551∙0,288∙ cos (4∙103 t
0,551∙0,288∙ cos (4∙103 t 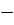 60°
60° 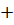 172°)
172°) 
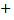 0,276∙1,473∙ cos (8∙103 t
0,276∙1,473∙ cos (8∙103 t  159,1°)
159,1°) 
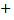 0,138∙7,261∙ cos (16∙103 t
0,138∙7,261∙ cos (16∙103 t  °
° 
 ∙5,618∙ cos (20∙103 t
∙5,618∙ cos (20∙103 t  °
° 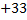 °)
°) 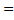
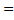 0,159∙cos(4∙103 t
0,159∙cos(4∙103 t 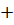 112°)
112°) 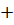 0,407∙cos(8∙103 t
0,407∙cos(8∙103 t 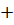 39,1°)
39,1°) 
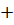 1,002∙cos(16∙103 t
1,002∙cos(16∙103 t 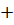 1,7°)
1,7°) 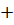 0,618∙cos(20∙103 t
0,618∙cos(20∙103 t 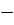 87°), B.
87°), B.
На рис. 1.7 представлены графики спектров амплитуд и фаз входного (а) и выходного (б) напряжений.
 а)
а)
 б)
б)
Рис. 1.7
Задание 2.
Расчёт LC -фильтра
Рассчитать двусторонне нагруженный LС-фильтр, полагая, что его элементы имеют пренебрежимо малые потери.
Исходные данные.
Код выполнения для варианта Б- 21. Следовательно, фильтр верхних частот (ФВЧ) с характеристикой Баттерворта
Исходные даны для расчёта ФВЧ с характеристикой Баттерворта:
a0 =17,0 дБ -минимально допустимое рабочее ослабление (затухание) в полосе задерживания;
f0=4,5M кГц=21кГц – граничная частота полосы пропускания для ФВЧ;
fk=3M кГц=15кГц – граничная частота полосы задерживания для ФВЧ;
∆a=3 дБ – неравномерность характеристики ослабления;
R1=100N Ом=100 Ом -внутреннего сопротивления источника на входе фильтра.
Решение.
В работе необходимо выполнить расчет LC-фильтра верхних частот удовлетворяющего равноволновой характеристике Баттерворта. При этом в полосе задержания затухание не должно быть меньше aQ=17дБ. В полосе пропускания - неравномерность ослабления должна быть не хуже ∆a=3 дБ (рисунок 2.1).
| a, дБ |
| Рисунок 2.1- Требования к характеристике затухания фильтра верхних частот |
| a0 |
| ∆ a |
| fk f0 |
| f, Гц |
При расчете LC фильтров используют методику, основанную на расчете низкочастотного фильтра прототипа (ФПНЧ), с последующим преобразованием его к требуемому виду. Воспользуемся данной методикой при расчете требуемого фильтра верхних частот.
В начале определяется порядок ФПНЧ:
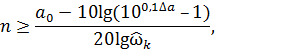
Где 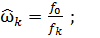 - нормированная частота для ФВЧ.
- нормированная частота для ФВЧ.
Подставляем исходные данные и вычисляем необходимый порядок фильтра:

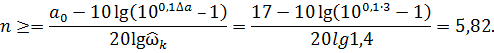
 Примем порядок фильтра n=6.
Примем порядок фильтра n=6.
Для ФПНЧ порядка п = 6 схема будет иметь вид, представленный на рисунке 2.2.

Данному порядку фильтра и виду характеристики по справочникам выбирают нормированные значения элементов. Так для фильтра 6-го порядка с характеристикой Баттерворта нормированные коэффициенты имеют следующие значения:
| n | |
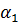
| 0,5176 |
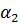
| 1,4140 |
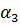
| 1,9320 |

| 1,9320 |
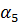
| 1,4140 |
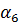
| 0,5176 |
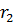
| 1,0000 |
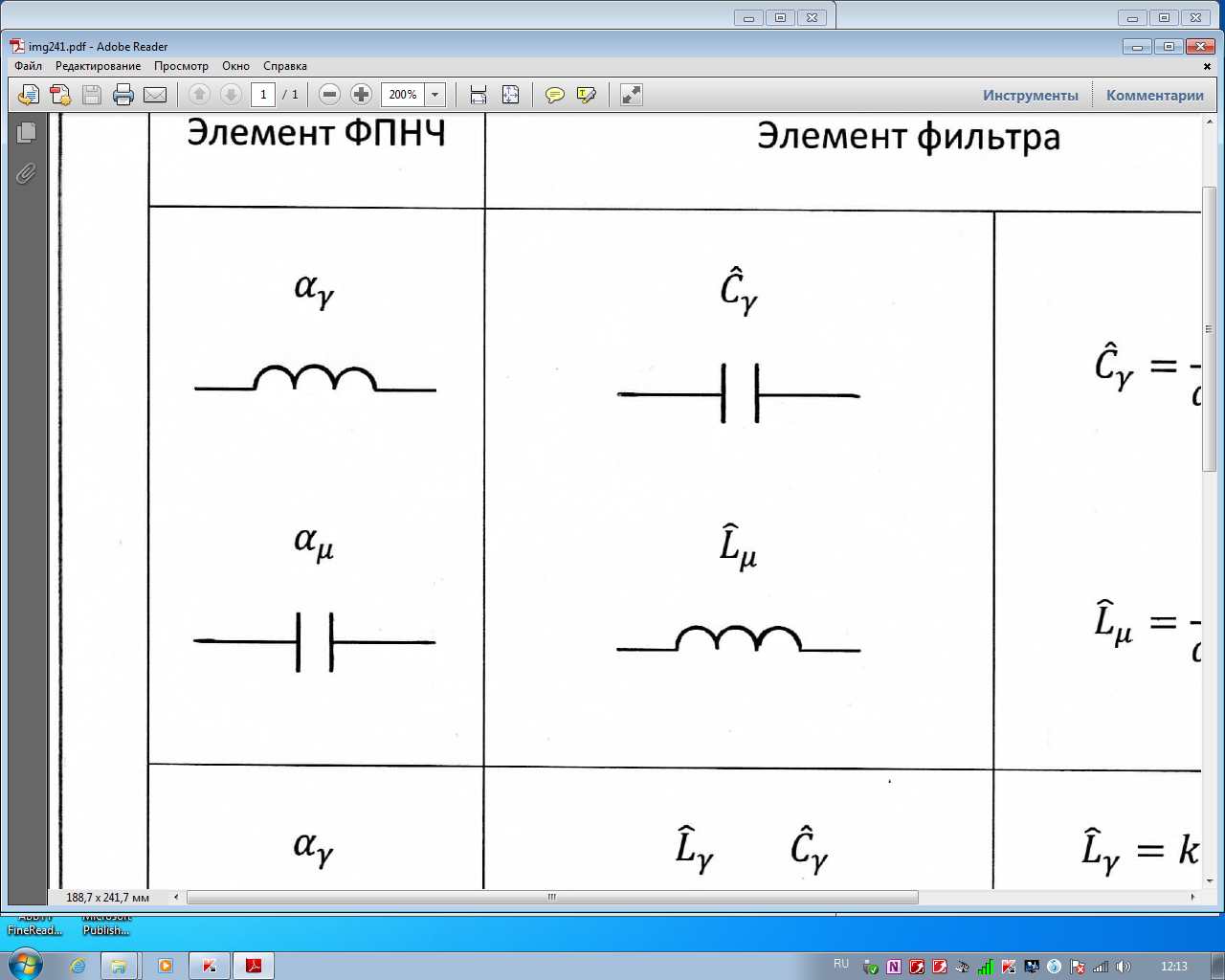
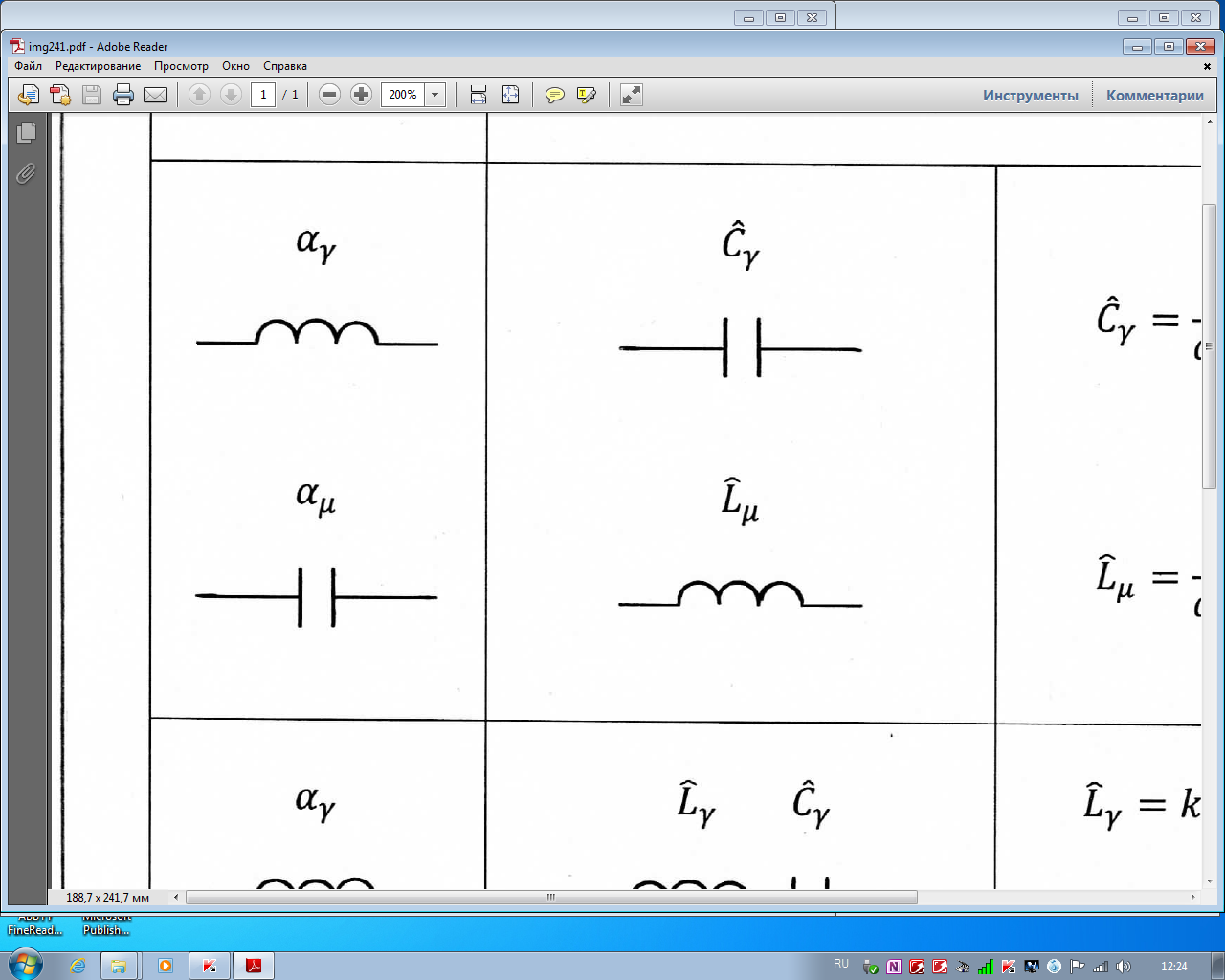
Выполняем переход от ФПНЧ к требуемому по заданию ФВЧ. Для этого необходимо на схеме ФПНЧ выполнить замену емкостей на индуктивности, и наоборот согласно таблице 2.1. В результате реальная схема ФВЧ примет вид представленный на рисунке 2.3.
Таблица 2.1- Преобразование элементов ФПНЧ в ФВЧ
| Элемент ФПНЧ | Элемент фильтра | Тип фильтра | |
| 
|
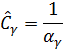
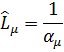
| ФВЧ |
Для вычисления номинальных значений параметров, т.е. значений соответствующих заданным величинам внутреннего сопротивления генератора 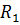 и частоты
и частоты 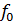 , следует воспользоваться формулами:
, следует воспользоваться формулами:

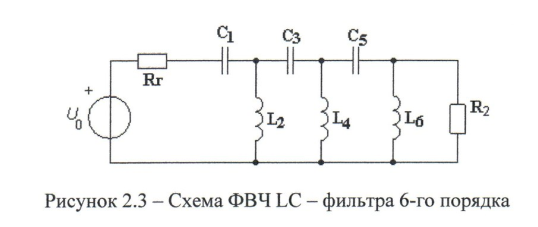
Вычисляем параметры номинальных элементов ФВЧ:
- находим нормированные значения элементов фильтра:
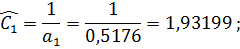





- вычисляем номинальные значения элементов:


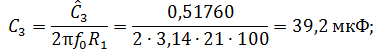
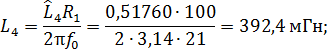

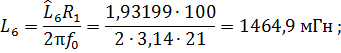
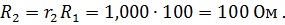
Вычислим величину затухания на границе полосы задержания. Величина ослабления определяется по аналогичному выражению, которое было использовано при расчете порядка фильтра:
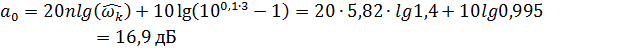
Для построения качественного графика воспользуемся программой моделирования FASTMEAN. Схема модели фильтра представлена на рисунке 2.4. В результате анализа частотной характеристики фильтра была получена АЧХ представленная на рисунке 2.5.
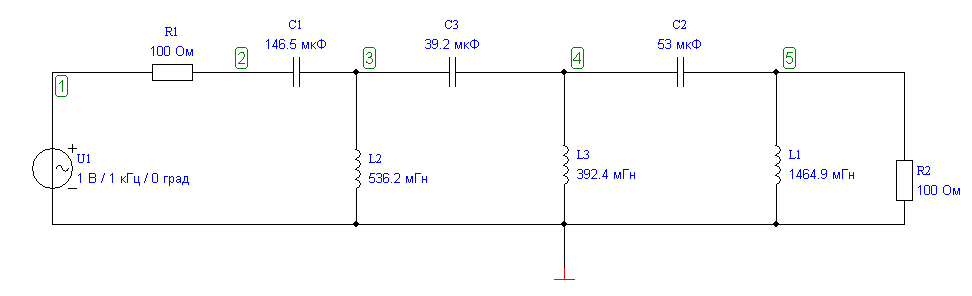

По АЧХ фильтра видим, что ожидаемое ослабление составит не менее в полосе задержания.


На рисунке 2.6 представлена результирующая схема ФВЧ, а в таблице 2.2 - значения элементов фильтра.
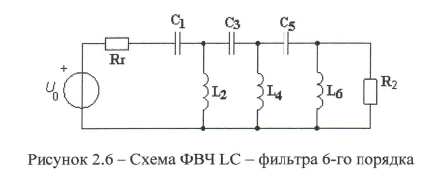
Таблица 2.2 Номиналы элементов фильтра
| R1, Ом | С2„ мкФ | 12,мГн | С3, мкФ | L4,мГh | С5, мкФ | L6, мГн | R2, Ом |
| 146,5 | 536,2 | 39,2 | 392,4 | 53,0 | 1464,9 |
Список использованной литературы
1. Белецкий А.Ф. Теория линейных электрических цепей: Учебник. 2-е изд. - СПб.: Издательство «Лань», 2009. - 544 с.
2. Бакалов В.П., Дмитриков В.Ф., Крук Б.И. Основы теории цепей: Учебник для вузов; Под редакцией В.П. Бакалова. 3-е изд. - М.: Горячая линия - Телеком, 2009. - 596 с.