Кусочно-полиномиальные функции

Интерполяция

Интерполяция – один из способов аппроксимации данных. В простейшем (одномерном) случае задача интерполяции [1-3] состоит в следующем: заданы точки (x_i, y_i), 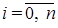, и требуется найти функцию j(x), которая проходит через эти точки (см. рис. 1), т.е.

j(x_i)= y_i, 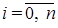. (1)

Точки (x_i, y_i) называют узлами интерполяции, а функцию j(x) – интерполирующей функцией или интерполянтом. Вид функции j(x) определяет способ интерполяции. На практике в качестве интерполирующей функции j(x) часто используются алгебраические полиномы различного вида, так как полиномы легко вычислять, дифференцировать и интегрировать. При этом интерполяция носит название полиномиальной.

Рассмотрим задачу линейной интерполяции. При этом интерполирующая функция имеет следующий вид:

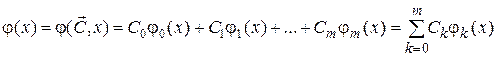, (2)

где j₀(x), j₁(x), …, j _m (x) – базисные функции.

Используя условие (1) и выражение (2), получаем систему уравнений

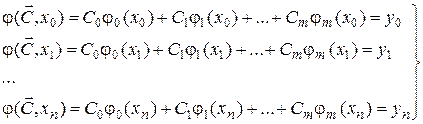(3)

Единственное решение системы (3) существует при двух условиях:

1) число точек (x_i, y_i), 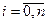равно числу коэффициентов С_k, ;

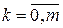2) система уравнений (3) должна быть невырожденной, т.е. определитель системы D ¹0.

Таким образом, если выполняются вышеуказанные условия, то через точки (x_i, y_i) проходит единственная функция .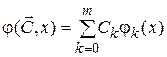

В случае линейной полиномиальной интерполяции базисные функции имеют следующий вид: j₀(x)= x ⁰=1, j₁(x)= x ¹= x, j₂(x)= x ², …, j _m (x)= x^m. Интерполирующая функция при этом имеет вид полинома степени m: j(x)= P_m (x)= C ₀ + C ₁ x + C ₂ x ² + … + C_m x ^m и, следовательно, система (3) примет вид

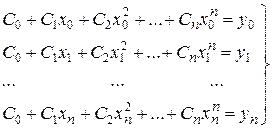(4)

В матричной форме систему (4) можно переписать как А*C = B, где

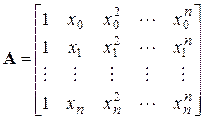– матрица Ван дер Монда; ; .

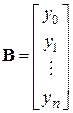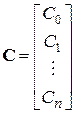Решением системы (4) будет вектор коэффициентов полинома С. Так как определитель матрицы Ван дер Монда всегда отличен от нуля (при x_i ¹ x_j), то решение системы (4) – единственное. Для решения системы (4) необходимо найти обратную матрицу A. В этом случае решением (4) будет C = A ^–1* B.

Вывод: Таким образом, через заданные на интервале [ a, b ] точки (x_i, y_i), всегда можно провести единственный интерполяционный полином j(x)= P_n (x)= C ₀ + C ₁ x + + C ₂ x ² + … + C_n x ⁿ, коэффициенты которого находятся в результате решения системы (4).

 

Пусть ординаты узлов интерполяции вычислены как значения некоторой заданной функции f: y _i= f (x_i) Выражение (1) определяет поведение функции j(x) только в узлах интерполяции (x_i, y_i), 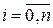. Между узлами j(x) может вести себя произвольным образом, сколь угодно далеко, в принципе, отклоняясь от зависимости f (x). Определить погрешность приближения можно, используя выражение для абсолютной ошибки e=| f (x) – j(x) |.

Ошибка полиномиальной интерполяции. Лучший способ проверить качество интерполяции – вычислить значения интерполирующей функции в большом числе точек и построить график. Однако в некоторых ситуациях качество интерполянта можно проанализировать. Предположим, что величина y_i представляет собой точные значения известной функции f (x) в точках x_i. Пусть P_n (x) – единственный полином n -й степени, интерполирующий функцию по этим точкам (x_i, y_i), 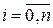. Предположим, что во всех точках х Î[ a, b ] функция f (x) имеет (n +1) непрерывную производную. Тогда можно показать [1, 2], что абсолютная ошибка интерполяции e(x)=| f (x)– P_n (x) | определяется выражением

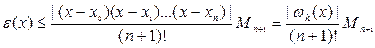, (5)

где 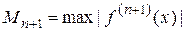- максимальное значение (n +1)-й производной функции f (x) на интервале [ a, b ]; .

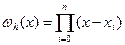Теперь посмотрим, что получится, если интерполировать известную функцию f (x) все в большем и большем числе точек на фиксированном интервале. Выражение для погрешности (5) состоит из трех разных частей; факториал и произведение разностей с увеличением n уменьшают ошибку, но порядок производной при этом растет. Для многих функций величина M_{n +1} увеличиваются быстрее, чем (n +1)!. В результате полиномиальные интерполянты редко сходятся к обычной непрерывной функции. Практический эффект выражается в том, что интерполирующий полином высокой степени может вести себя "плохо" в точках, отличных от узлов интерполяции (x_i, y_i), 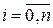. Поэтому на практике часто используют интерполянты степени не выше 5-6.

Рисунок 2 – интерполяция функции Рунге полиномом степени n

Примером может служить функция Рунге [4] вида R (x)=1/(1+25 x ²), график которой представлен на рис. 2. С увеличением порядка интерполирующего поли­нома при равномерном распределении узлов интерполяции на интервале [–1, 1] происходит ухудше­ние качества приближения на краях интервала. Это объясняется тем, что производные R (x), которые фигурируют в выражении для погрешности интерполя­ции (5), быстро растут с увеличением числа n.

 

Точность приближения зависит не только от числа узлов интерполяции (т.е. порядка интерполирующего полинома), но и от их расположения на интервале [ a, b ]. В простейшем случае выбирается равномерное расположение точек (x_i, y_i), 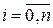на интервале [ a, b ] с шагом D x =(b – a)/(n –1). Однако, как показывает практика, равномерное расположение не является оптимальным с точки зрения лучшего приближения j(x) к зависимости f (x). Более оптимальным для полиномиальной интерполяции является расположение узлов на интервале [ a, b ] по формуле Чебышева

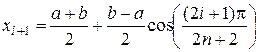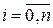, . (6)

Выражение (6) определяет так называемое оптимальное распределение узлов интерполяции на интервале [ a, b ].

 

 

Кусочно-полиномиальные функции

 

Функция f(х) называется кусочно-полиномиальной, если на каж­дом из отрезков 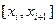(i = 1,2,...,n-1; х ₁ < х₂ < … < х_п) она представляет собой многочлен

f_i(x) = а_i1 х^k + а_i2 х^k-1 + …+ а_ik х + а_{i,k +1}.

Часто удобно иметь дело не с многочленами f(х), а с многочленами

h_i(x) = b_i1 х^k + b_i2 х^k-1 + …+ b_ik х + b_{i,k +1},

полученными из f_i(х) сдвигом отрезка 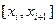в новое положение 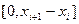. Связь коэффициентов этих двух систем многочленов устанавливается очевидным равенством

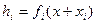
Для представления кусочно-полиномиальных функций система MATLAB использует структуру специального вида. Эту структуру мы будем называть рр-представлением.

Функция pp= mkpp (x,B) создает рр-представление кусочно-полиномиальной функции по узлам х и коэффициентам многочленов В. Вектор х должен иметь длину n и содержать координаты узлов х ₁, х_2,, …, х_п. Матрица В должна иметь размеры (n-1) х(k + 1) и содержать коэффициенты многочленов h_i (х):

Функция [x,B]= unmkpp (pp) возвращает вектор узлов х и матрицу коэффициентов В по представлению рр кусочно-полиномиальной функции.

Функция yy= ppval (pp,xx) возвращает набор значений уу в точках хх кусочно-полиномиальной функции, заданной представлением pp.

Пример. Рассмотрим кусочно-квадратичную функцию

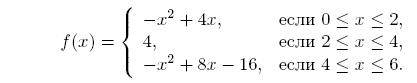
После сдвига получаем

h (x) = -x² + 4x,

h₂ (x) = 4,

h₃ (x) = - (х + 4)² + 8(x + 4) - 16 = -х² + 4.

Нарисуем графики функций h_i (x) и f (x):

xx=[0:0.05:2];

yyl=polyval ([-1 4 0],xx);

yy2=polyval([0 0 4],xx);

yy3=polyval ([-1 0 4],xx);

Subplot(2,3,2)

Plot(xx,yyl,xx,yy2,xx,yy3)

axis([0 2 0 5])

Title('h_l(x), h_2(x), h_3(x) ')

x= [0 2 4 6];

A=[-1 4 0; 0 0 4; -1 0 4];

pp=mkpp(x, A);

xx=[0:0.05:6];

yy=ppval(pp_, xx);

Subplot(2,1,2)

plot(xx,yy);

axis([0 6 0 5])

Title('f(x)')