Кусочно-полиномиальная интерполяция

Следующие функции по узлам х и значениям в узлах у находят кусочно-полиномиальный интерполянт и возвращают его значения в точках хх:

· interp1(x,y,xx, 'nearest') использует ступенчатую интерполя­цию.

· interp1 (x,y,xx) или interp1 (x,y,хх,'linear') строит кусочно-линейный интерполянт,

· spline(x,y,xx) или interp1 (x,y,xx, 'spline') находит кубиче­ский сплайн,

· pchip(x,y,xx) или interp1 (x,y,xx,'pchip') или interp1 (x,y,xx,'cubic') ищет эрмитов кубический интерполянт.

При равномерной сетке х можно использовать более быстрые мето­ды “со звездочкой”: nearest*, linear*, spline*, pchip* - например:

interp1(x,y,xx,'spline*')

Кроме этого, функции pp=spline(x,y) pp=pchip(x,y) возвращают pp-представление для сплайн-интерполянта и эрмитова кубического интерполянта соответственно.

Пример. Построим интерполянты функции Рунге по 9 точкам и вычислим абсолютные ошибки интерполяции:

x=-1:0.25:1;

y=1./(1+25*x.^2);

xx=-1:.01:1;

yy=1./(1+25*xx.^2);

yn=interp1(x,y,xx,'nearest');

yl=interp1(x,y,xx,'linear');

yc=interp1(x,y,xx,'cubic');

ys=interp1(x,y,xx,'spline');

plot(x,y,'o', xx,yy, xx,yn, xx,yl_, xx,yc_, xx,ys)

Legend('data',...

'function',...

'nearest' ,...

'linear',...

'cubic',...

'spline', 2);

Max(abs(yn-yy))

Max(abs(yl-yy))

Max(abs(yc-yy))

Max(abs(ys-yy))

Мы видим, что минимальную ошибку (0.02) дал кубический интерпо­лянт, на втором месте -- сплайн (0.06), далее— линейный интерполянт (0.064) и на последнем месте -- ступенчатый интерполянт (0.31).

В следующих разделах рассмотрим несколько подробнее эти способы интерполяции.

 

Эрмитов кубический интерполянт

Предположим, что в точках из­вестны не только значения функции , но и их произ­водные d ₁, d ₂...., d _n. Заменяя функцию g(х) на каждом из отрезков [x_i x_i+1] кубическим многочленом c_i(x), таким, что

мы получим эрмитов кубический интерполянт

.

Очевидно, что эрмитов кубический интерполянт имеет непрерывную производную. Из дальнейшего будет следовать, что по значениям функ­ции и ее первой производной в узлах, кубический интерполянт опреде­ляется единственным образом. Если g (x) имеет непрерывную четвертую производную, то погрешность интерполяции можно оценить как

где h-- максимальное расстояние между смежными узлами. Кроме то­го, можно показать, что

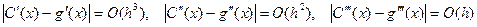
Для вывода расчетных формул рассмотрим отрезок [0,1] и условия

Легко проверить, что единственным многочленом степени не выше 3, удовлетворяющим этим условиям, является многочлен

,

где

 

Чтобы перейти к произвольному отрезку [ a, b ] достаточно рассмотреть р(а+(b-а)х).

Функция, которая находит рр-представление для кубического эрми­това интерполянта, может выглядеть следующим образом:

function p=cubic1(x,y,d);

n=length(x);

a=zeros(n-1,4);

for i=1:n-1

a(i,1)=2*y(i)-2*y(i+1)+d(i)+d(i+1);

a(i,2)=-3*y(i)+3*y(i+1)-2*d(i)-d(i+1);

a(i,3)=d(i);

a(i,4)=y(i);

a(i,1)=a(i,1)/(x(i+1)-x(i))^3;

a(i,2)=a(i,2)/(x(i+1)-x(i))^2;

a(i,3)=a(i,3)/(x(i+1)-x(i));

end;

p=mkpp(x,a);

Приведем пример использования этой функции:

x= [0 1 2 3 4 5];

y= [0 1 1 2 3 3];

d0= [0 0 0 0 0 0];

d1=[1 1 1 1 1 1];

p0=cubic1(x,y,d0);

p1=cubic1(x,y,d1);

xx=0:.05:5;

yy0=ppval(p0,xx);

yy1=ppval(p1,xx);

plot(x,y,'o',xx,yy0,xx,yy1);

Grid

Если значения производных в узлах не известны, то можно попро­бовать заменить их приближениями. Сложный алгоритм выбора d, реализован в стандартной функции pchip. Если х, у — абсциссы и ординаты узлов интерполяции, то ко­манда yyp=pchip(x,y,хх) строит кубический интерполянт и возвраща­ет его значения уур в точках хх. Построенный интерполянт обладает следующими особенностями:

· если на некотором отрезке данные монотонны, то монотонным будет сам интерполянт,

· если в некоторой точке данные имеют локальный экстремум, то ло­кальный экстремум в той же точке будет и у интерполянта,

Проверим это

x =0:8;

y = [0 1 1 2 3 4 3 2 1];

xx=0:.05:8;

yyp=pchip(x,y,xx);

plot(x,y, 'o',xx,yyp);

 

Сплайны

Не всегда кубический эрмитов интерполянт может нас удовлетво­рить: в общем случае его вторая производная разрывна и, следова­тельно, график не достаточно гладок. Пусть, как и раньше, функция g (x) в точках принимает значения соответственно. На каждом из отрезков [x_i x_i+1]заменим g (x) кубической функцией c_i(x),такой, что . Кусочно-кубическая функция

называется кубическим сплайном (или, просто, сплайном), если она вез­де имеет непрерывную вторую производную. Для того, чтобы сплайн определялся единственным образом, зададим также значения первой производной в концах рассматриваемого интервала. Сплайн, определя­емый условиями

называется естественным.

Если g(х) имеет непрерывную четвертую производную, то погреш­ность интерполяции можно оценить как

где h - максимальное расстояние между смежными узлами.

Функция yyp=spline(x,y,xx) по значениям у в узлах х строит есте­ственный сплайн и возвращает его значения уур в точках хх. Эта функ­ция выбирает такие значения первой производной в концевых точках, чтобы третья производная в узлах х ₁ и х_{n -1} была непрерывна.

Несмотря на то, что графики сплайнов более гладкие нежели графи­ки кубических интерполянтов, не всегда использование сплайнов дает удовлетворительные результаты.

Пример. Рассмотрим, например, случай, когда данные описывают некоторый естественный монотонный процесс:

x= [0 1 2 3 4 5];

y= [0 1 1 2 3 3];

xx=0:.05:5;

yyp=pchip(x,y,xx);

yys=spline(x,y,xx);

plot(x,y,'o',xx,yyp,xx,yys);

Сплайн оказался немонотонным, кубический интерполянт, который на­шла функция pchip, - монотонным.