Однако I1 и I2 — не единственные токи, протекающие в обмотках трансформатора. Кроме токов нагрузки в обмотках трансформаторов обнаруживаются еще и другие токи, которые замыкаются внутри отдельных проводов и между параллельными ветвями обмоток; эти токи в отличие от токов нагрузки не выходят за пределы обмоток. Токи, замыкающиеся внутри отдельных проводов, называют вихревыми (аналогично токам внутри пластин магнитной системы). Токи, замыкающиеся между параллельно соединенными обмотками или частями обмоток, называют циркулирующими. Эти токи вызываются полем рассеяния, т. е. той частью магнитного поля трансформатора, силовые линии которой сцепляются не со всеми, а только с частью витков обмоток и проходят главным образом в немагнитной среде (в воздухе, масле и т. п.). При расчете потерь в обмотках реальный ток, неравномерно распределяющийся по сечению проводов и между параллельными ветвями обмоток, обычно рассматривают как сумму трех токов: - тока нагрузки, равномерно распределяющегося по поперечному сечению и между параллельными ветвями; - циркулирующего тока, замыкающегося внутри контура, образованного параллельными ветвями; - вихревого тока, замыкающегося только в пределах каждого провода. При этом сумма потерь от трех указанных токов равна реальным потерям в обмотках трансформатора. Кроме потерь в обмотках поля рассеяния вызывают потери в стенках бака, прессующих кольцах, ярмовых балках и других элементах конструкции трансформатора. Добавочные потери снижают эффективность трансформатора; с ними ведется постоянная борьба с целью добиться их минимальной величины. Итак, в трансформаторе различают потери активной мощности, не зависящие от нагрузки (Р0); нагрузочные (Рнагр) и добавочные (Рдоб) потери, определяемые режимом работы (величиной нагрузки) трансформатора: ΣР = Р0 + Рнагр + Рдоб.
|
|
Постоянные и переменные потери. Уравнение баланса мощности в цепи с трансформатором
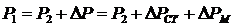 ,
,
где  – активная мощность, поступающая из сети питания (от источника);
– активная мощность, поступающая из сети питания (от источника); 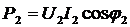 - активная мощность потребителей;
- активная мощность потребителей; 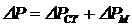 – суммарная мощность потерь в трансформаторе;
– суммарная мощность потерь в трансформаторе; 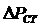 — мощность потерь в стали;
— мощность потерь в стали; 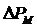 — мощность потерь в проводах обмоток.
— мощность потерь в проводах обмоток.
Мощность потерь в стали магнитопровода из-за гистерезиса и вихревых токов 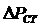 зависит от амплитуды магнитного потока
зависит от амплитуды магнитного потока 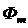 , а так как
, а так как 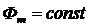 , то мощность потерь в стали не изменяется, т. е. не зависит от нагрузки при постоянном значении напряжения питания
, то мощность потерь в стали не изменяется, т. е. не зависит от нагрузки при постоянном значении напряжения питания 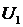 . Эти потери составляют 1—2 % номинальной мощности. Мощность потерь в проводах обмоток зависит от нагрузки, так как
. Эти потери составляют 1—2 % номинальной мощности. Мощность потерь в проводах обмоток зависит от нагрузки, так как 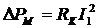
Зависимость потерь в стали и меди от коэффициента нагрузки 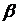 показана на рис. 2.16.
показана на рис. 2.16.
Коэффициент полезного действия трансформатора. КПД трансформатора можно рассчитать по формуле
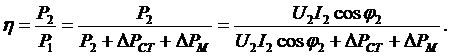
Так как коэффициент нагрузки 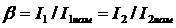 и в опытах холостого хода и короткого замыкания было получено, что
и в опытах холостого хода и короткого замыкания было получено, что 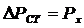 , а
, а 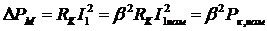 , то КПД
, то КПД
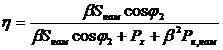 . (2.21)
. (2.21)
Годовой КПД трансформатора. Если в течение года часть времени трансформатор работает в режиме холостого хода, то эксплуатационный или годовой КПД
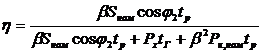 , (2.22)
, (2.22)
где 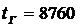 — число часов в году;
— число часов в году; 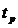 — число часов работы трансформатора при постоянной нагрузке.
— число часов работы трансформатора при постоянной нагрузке.
Если нагрузка трансформатора изменяется в течение суток так, что в течение времени 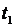 коэффициент нагрузки составляет
коэффициент нагрузки составляет 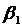 , в течение времени
, в течение времени 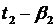 и т.д., то среднесуточный КПД
и т.д., то среднесуточный КПД
|
|
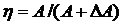 , где
, где 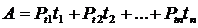 (
( 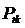 – активная мощность потребителей в течение времени
– активная мощность потребителей в течение времени 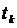 );
);
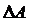 — потери, в трансформаторе за сутки, т.е.
— потери, в трансформаторе за сутки, т.е.
 ,
,
где
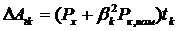 .
.
Зависимость КПД трансформатора от нагрузки. Из (2.21) можно найти значение нагрузки 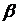 , при котором КПД максимален. Приравняв нулю производную
, при котором КПД максимален. Приравняв нулю производную 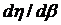 , получим:
, получим:
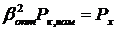 .
.
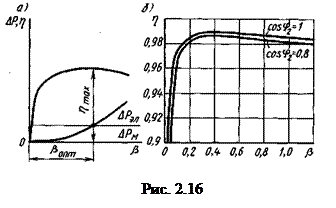
Это значит, что КПД 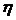 максимален при равенстве мощностей потерь в проводах обмоток и в стали. Следовательно, оптимальный коэффициент нагрузки
максимален при равенстве мощностей потерь в проводах обмоток и в стали. Следовательно, оптимальный коэффициент нагрузки
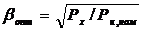 .
.
 Обычно для трансформатора
Обычно для трансформатора 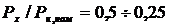 и, значит,
и, значит, 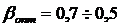 . Таким образом, наибольшее значение КПД трансформатора будет при нагрузке 70—50 % от номинальной.
. Таким образом, наибольшее значение КПД трансформатора будет при нагрузке 70—50 % от номинальной.
Зависимость КПД от нагрузки, построенная согласно (2.21), показана на рис. 2.16. Общая номинальная мощность установленных силовых трансформаторов в 4-6 раз превышает мощность генераторов, поэтому КПД трансформаторов имеет важное значение для рационального использования энергетических ресурсов. Максимальный КПД силовых трансформаторов доходит до 99,5 %..