Плотность потока нейтронов

Следующая из основных характерис­тик нейтронных полей - плотность потока нейтронов (Ф) - является поп­росту произведением первых двух: плотности нейтронов на их скорость:

Ф = n ^. v (2.3.8)

По физическому смыслу эта величина - суммарный секундный путь всех нейтронов в 1 см³среды. Однако размерность плотности потока - нейтр/см² с - может привести к путанице в попытках обна­ружить физический смысл этой величины в самой размерности: сразу воображается некая плоская площадка размером в 1 см², через которую ежесекундно проходит определённое число нейтронов. Такому представлению способствует прошлый опыт изучения сходным образом звучащих величин иной физической природы: плотности потока жидкости (из гидродинамики), плот­ности магнитного потока и плотности потока электронов в проводнике (из электродинамики), плотности теплового потока на теплоотдающей поверх­ности (из теплотехники) и другими. Аналогия плотности потока нейтронов с перечисленными величинами несостоятельна, так как все эти ве­личины характеризуют направленный перенос энергии, а нейтроны в единич­ном объёме среды движутся не направленно, а хаотично по всем возможным направлениям.

На первый взгляд эта характеристика вообще кажется лишней, т.к. она - простая комбинация двух других характеристик нейтронных полей - пло­тности (n) и скорости (v) нейтронов. Однако, самое простое рассуждение о том, что секундное количество актов любой нейтронной реакции в 1 см³ среды должно быть прямо пропорционально величинам и плотности нейтронов (n), и скорости их переноса (v), а, следовательно, - величине плотности потока нейтронов (Ф), даёт этой характеристике право на существование. Действительно, чем больше плотность нейтронов n и чем больше скорость их перемещения v, тем больше шансов имеют все эти нейтроны в 1см³ сре­ды провзаимодействовать с ядрами среды в течение 1 с и вызвать те или иные нейтронные реакции.

1.4 Выравнивание тепловыделения в активной зоне реактора

Из рассмотрения реакторов с однородной активной зоной и отражателем следует, что существует значительная неравно­мерность в распределении потока нейтронов (энерговыделения) по объему реактора. Так, в цилиндрической активной зоне реак­тора максимальная тепловая нагрузка превышает среднюю бо­лее чем в 3 раза. Поэтому необходимо применять какие-либо меры по выравниванию нейтронного потока, чтобы уменьшить коэф­фициенты неравномерности. Известно большое число способов уменьшения неравномерности энерговыделения в современных энергетических реакторах. Все они сводятся к выравниванию числа актов деления ядер топлива по объему активной зоны (физическое профилирование). Добиться требуемого выравнивания можно либо чисто внешними средствами (например, рабочими органами СУЗ, выго­рающими поглотителями и т. д.), либо изменяя концентрацию ядерного топ­лива по объему реактора. В современных реакторах чаще используют второй способ как наибо­лее эффективный. Для выравнивания тепло­выделения используются следующие способы:

1) применение эффективных отражателей нейтронов, расположенных вокруг активной зоны, позволяющих уменьшить утечку нейтронов и тем самым выровнять распределение плотности потока тепловых нейтронов и соот­ветственно тепловыделение;

2) создание многозонных реакторов, в которых распреде­ление ядер ²³⁵U по радиусу актив­ной зоны выполнено таким обра­зом, чтобы изменение концентрации ядер ²³⁵Uбыло примерно обратно пропор­ционально изменению плотности потока нейтронов;

3) применение твердых и жидких поглотителей, изго­товленных из материалов, сильно поглощающих тепловые нейтроны. Поглотитель стремятся располагать по радиусу и высоте активной зоны таким образом, чтобы его концент­рация была прямо пропорциональ­на плотности потока нейтронов.

Рассмотрим выравнивание энер­говыделения с помощью распре­деления топлива. Наиболее просто это можно осуществить по радиусу реактора. Однако добиться на практике физического профилирования энергетиче­ских реакторов с помощью непрерывного изменения концентра­ции делящегося вещества весьма трудно по технологическим и конструктивным причинам.

В связи с этим возникает задача о зонном профилировании активной зоны, при котором концентрация делящегося вещества меняется скачком от зоны к зоне, оставаясь практически по­стоянной внутри каждой из них. Число зон и их размеры зави­сят в основном от принятого режима перегрузки. Обычно на практике ограничиваются двумя зонами: центральной и периферийной. Зонная компоновка активной зоны широко используется в реакторах типа ВВЭР, где свежее топливо, т. е. более обо­гащенное, располагается в перифе­рийной зоне, а выгоревшее, т. е. ме­нее обогащенное, находится в цент­ральной зоне.

Действие отражателя основано на том, что покидающие активную зону нейтроны попадают в окру­жающую среду и находятся в ней в хаотическом движении, так же как в самой активной зоне. Поэто­му часть нейтронов, отражаясь от ядер среды, может возвратиться обратно. Отсюда результирующая утечка нейтронов из активной зоны уменьшается. Отношение числа нейтронов, возвращающихся в ак­тивную зону в результате отраже­ния, к числу попадающих в отра­жатель нейтронов называют коэф­фициентом внутреннего от­ражателя нейтронов или альбедо β.

В ядерных реакторах на тепло­вых и промежуточных нейтронах в качестве отражателей используют­ся вещества, хорошо замедляющие и слабо поглощающие нейтроны, т. е. вещества-замедлители нейтро­нов. Они обладают самыми высо­кими альбедо; например, у слоя обычной воды толщиной 2L, где L — длина диффузии тепловых нейтронов, β=0,8, у слоя бериллия той же толщины β=0,9, у графита β=0,94 и у тяжелой воды β=0,98.

При этом в отражателе помимо отражения собственно тепловых нейтронов в активную зо­ну происходит замедление быстрых нейтронов, причем более эффектив­но, чем в самой активной зоне, где имеется определенная вероятность захвата нейтронов. Часть замедлив­шихся нейтронов возвращается в активную зону и еще больше повы­шает плотность потока тепловых нейтронов вблизи отражате­ля. Влияние отражателя, грубо говоря, сводится к уменьшению утечки нейтронов из активной зоны и соответственно к уменьшению критических размеров реакто­ра. Наиболее эффектив­ными отражателями являются слои, рас­положенные вблизи активной зоны. С уве­личением расстояния от границы активной зоны эффективность отражения нейтронов падает, так как уменьшается доля нейтро­нов, попадающих в удаленные слои отра­жателя. Поэтому оказывается, что эффек­тивность слоя отражателя толщиной Т≈1,5М [где М — длина миграции в отра­жателе] близка к эффективности слоя бесконечной толщины, и дальнейшее увеличение толщины отражателя бесполез­но. Для графита предельная тол­щина составляет около 90 см, для обыч­ной воды — приблизительно 10 см. При оценке отражателей толщиной, равной или большей 1,5М, можно принять, что эффек­тивная добавка равна длине миграции в материале отражателя.

Для каждого замедляющего вещества существует предельная тол­щина отражателя, превышение которой практически не сказы­вается на распределении потока тепловых нейтронов в актив­ной зоне. Эта предельная толщина отража­теля составляет:

для тяжелой воды.......80 см

графита..........120 см

Природная вода из-за сильного поглощения ею нейтронов не годится в качестве отражателя. Если толщина отражателя меньше 30% предельных значений, то эффективные добавки следует принимать равными толщине отражателя. При от­ражателе предельной толщины эффективные добавки можно принимать равными 50% толщины отражателя. Для промежу­точных значений толщины отражателя эффективные добавки можно находить линейной интерполяцией.

В современных энергетических реакторах одновременно применя­ются все перечисленные выше спо­собы выравнивания тепловыделе­ния. В результате достигаются следующие значения коэффициен­тов неравномерности: по радиусу 1,2-1,5; по высоте k_z= 1,3-1,5; по объему 1,5‑2,5. Например, в реакторе типа ВВЭР это дало возможность снизить коэффициент k_v в 2 раза: с 4,8 (реактор ВВЭР-210 на I блоке Нововоро­нежской АЭС) до 2,4 (реактор серийный ВВЭР-440).

В процессе работы реактора происходит выгорание топлива и поглотителя, соответственно изменя­ется распределение тепловыделения по активной зоне. Поэтому прово­дится изменение распределения по­глотителей во времени таким обра­зом, чтобы обеспечить минимизацию рассмотренных коэффициентов неравномерности.

1.5 Температурные эффекты в реакторе

Температурным эффектом реактивности реактора при рассматриваемой средней температуре теплоносителя в активной зоне называется величина изменения реактивности при его разогреве от 20^оС до этой температуры. Из определения сразу следует, что величина температурного эффекта реактивности при температуре 20^оСравна нулю. Этой условностью догово­рились определитьначало отсчетавеличины температурного эффекта. Поскольку в определении идёт речь об изменении реактивности, ве­личина температурного эффекта (как и всякая реактивность) обозначается символом ρ_t c нижним индексом "t", позволяющим отличать температурный эффект от реактивности любого другого происхождения. Почему ρ_t, а не Δρ_t, т.к. в определении речь идет обизменении реактивности? - Именно потому, что ρ_t(20^oC) = 0.

Поскольку из определения можно понять, что величина температурного эффекта - изменяющаяся с температурой величина, нелишне указать в обо­значении, какой температуре соответствует данныйтемпературный эффект реактивности, - то есть полное обозначение ТЭР, исключающее какую-либо неопределённость толкования этой величины, должно быть ρ_t(t). Поэтому и изменение реактивности при разогреве реактора от 20^о до произвольной средней температуры теплоносителя t будет равно:

Δρ_t(t) = ρ_t(t) - ρ_t(20^oC) = ρ_t(t) - 0 = ρ_t(t)

из-за чего величина температурного эффекта реактивности при любой средней температуре теплоносителя t обозначается не Δρ_t, апросто ρ_t.

Наконец, поскольку ТЭР есть изменениереактивности реактора, то и измеряется онв единицах реактивности (в а.е.р.). Первые из указанных единиц чаще встречаются в научной и технической литературе (как более простые, интернациональные, понят­ные всем), а вторые - в операторской практике (они удобны в расчетах).

В определении ТЭРзафиксировано, что аргументом для функции ρ_t(t) являетсясредняя температура теплоносителя. С первого взгляда это ка­жется неверным, так как температурное поле в гетерогенной активной зо­не энергетического ВВР очень неоднородно: в топливе твэлов температура выше, чем температура оболочек твэлов, а температура оболочек твэлов - выше температуры теплоносителя, а, главное, что во всех материалах ак­тивной зоны в силу действия теплотехнических законов даже в стационар­ном режиме реактора температуры распределеныпо-разномуи в различных пределах. А так как нам уже понятно, что каждый материалпо-своему от­зывается на одинаковые изменения температуры, это означает, что каждый материал активной зоны даже при одинаковых изменениях в них температу­ры вносит в общий температурный эффект реактивности свою лепту темпе­ратурных изменений реактивности,отличающуюся по величине от вкладов в ТЭР реактора других материалов. При имеющемся в реальных реакторахнеодинаковом разогреве топлива, замедлителя, теплоносителя и других кон­струкционных материалов активной зоны вклады каждого материала в общий температурный эффект реактивности тем более неоднозначны, и потому од­но лишь изменение средней температуры теплоносителя не может быть ответственным за полное температурное изменение реактивности всего реак­тора. Понятно, что температурное изменение реактивности реактора должно определятьсянекоторойсреднеэффективнойвеличиной температуры ак­тивной зоны, в которой учитывались бы "весовые коэффициенты" темпера­турных изменений реактивности каждого материала и неравномерность ра­зогрева каждого материала активной зоны.

Однако для определения такой температуры потребовалось бы решить задачу чрезвычайной сложности, более обширную, чем детальный теплотех­нический и нейтронно-физический расчеты всего реактора.

В качестве определяющей температуры для оценки температурного эф­фекта реактивностивынужденно принимается средняя температура теплоно­сителя, поскольку это температура,которую легко практически измерить. Серии термопар, поставленных на входе и выходе активной зоны, дают по­сле усреднения результатов измерений точное представление о величинах температур теплоносителя на входе и выходе из активной зоны, а средняя арифметическая их величина

t_т^ср = 0.5(t_т^вх + t_т^вых) (10.1.1)

- достаточно точное представление о средней температуре теплоноси­теля в активной зоне; хотя от входа к выходу теплоноситель увеличивает температурунелинейно по длине ТВС, из-за небольшой разницы входной и выходной температур теплоносителя (не более 30 - 35^оС) среднеарифмети­ческое значение температуры теплоносителя почти не отличается отсредневзвешенного её значения в активной зоне. К тому же практически измерение крайних температур теплоносителя иполучение электрического сигнала, пропорционального величине средней температуры теплоносителя, не представляет собой сложной технической задачи по сравнению с измерением даже лока­льной температуры топлива (для чего понадобилось бы сверлить герметич­ную оболочку твэла для осуществления вывода электрического сигнала от микротермопары внутри твэла).

Более того, приняв в качестве аргумента для функции температурного эффекта реактивностиреактора ρ_t(t_т) среднюю температуру теплоносителя t_т, мы по крайней мере получаем возможностьэкспериментально измерятьвеличину составляющей общего температурного эффекта реактивности реак­тора, которая определяется только изменением температуры теплоносителя ( для этого надо медленно, равномерно разогревать работающий на минимально-контролируемом уровне мощности (МКУМ) реакторот постороннего источника тепла с тем, чтобы температура топлива в его твэлахнезначите­льно отличалась от температуры теплоносителя).

Если эксплуатировать ВВР от малых уровней мощности и до номиналь­ной её величиныпри постоянном расходе теплоносителя через его актив­ную зону, то появляется возможность экспериментально измерить величины температурного эффекта реактивности реактора путём его медленного или ступенчатого разогревасобственным теплом(путем медленного увеличения мощности реактора, обеспечивающегомалую скорость разогрева - не более 10^оС/час, - при которой нестационарный режим разогрева реактора можно с должной степенью точности считатьквазистационарным ). При этом изме­ренная экспериментально зависимость ρ_t(t_т) будетоднозначной (по край­ней мере, на данный момент кампании), поскольку изменение среднеэффек­тивной температуры топлива на разных уровнях мощности в процессе разо­грева реактора будет в силу теплотехнических закономерностей взаимно­однозначно связано с изменением среднеэффективной температуры теплоно­сителя.

Зависимость температурного эффекта реактивности от средней температуры теплоносителя ρ_t(t_т) является очень сложной функцией. Поэтому использо­вание аналитического выражения ρ_t(t_т) (допуская, что его можно получить в годном для пользования виде) для оператора реакторной установки было бы неудобным: чем сложнее формула, которая её описывает, тем более гро­моздкие расчеты приходилось бы вести при решении простой задачи о тем­пературном изменении реактивности.

Но оператору зависимость ρ_t(t_т) нужна для практического использо­вания, и пусть она будет не идеально-точной, но представлена она долж­на быть в такой форме, которая позволяла бы быстро оценивать величины температурных эффектов реактивности при различных средних температурах теплоносителя и оперативно находить температурные изменения реактивности реактора при заданных изменениях температур теплоносителя, не про­изводя при этом громоздких вычислений. Такой формой представления фун кции ρ_t(tτ) является ее график.

График ρ_t(t_т) в эксплуатационной практике чаще называют просто кривой температурного эффекта реактивности (кривой ТЭР) реактора.

Хорошо и в приемлемом масштабе вычерченная по результатам послед­них нейтронно-физических измерений кривая ТЭР позволяет быстро снять величину ТЭР при нужной температуре теплоносителя и в считанные секун­ды вычислить температурное изменение реактивности при конкретном изме­нении средней температуры теплоносителя от t_т1 до t_т2:

Δρ_t = ρ_t(t_т2) - ρt(t_т1), (10.1.2)

независимо от того, идет ли речь о разогреве реактора (t_т2 > t_т1) или о его расхолаживании (t_т2 < t_т1). Следуя формуле (10.1.2), мы ни­когда не ошибемся в знаке температурного изменения реактивности: поло­жительная величина Δρ_t означает, что при изменении Δt_т = t_т2-t_т1 имеет место высвобождение реактивности, а при Δρ_t < 0 - потеря реактивности за счёт изменения температуры активной зоны (отсчитываемого по измене­нию средней температуры теплоносителя).

Энергетическим реакторам свойственны кривые ТЭР трёх качественных типов (или форм), показанных на рис.10.1

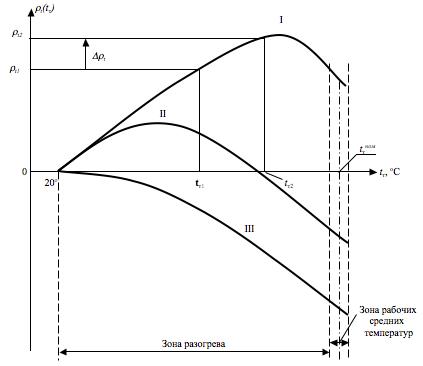
Кривая первого типа отличается восходящим до максимума характером с последующим снижением величины ТЭР, но вся она лежит в положительном квадранте величин ТЭР.
Кривая второго типа также имеет максимум, но в области значитель­но меньших температур, после чего она падает до нуля и переходит в от­рицательный квадрант величин ТЭР.
Кривая третьего типа имеет чисто падающий характер и целиком рас­полагается в отрицательном квадранте ТЭР при любых средних температу­рах теплоносителя.
Величины температурного эффекта, как следует из рис.10.1, могут быть положительными, отрицательными и даже принимать нулевые значения при некоторых (отличных от 20^оС) температурах теплоносителя.

Несколько слов о градации температур теплоносителя в энергетичес­ких реакторах. Любой энергетический реактор предназначается для работы при определенной (расчетной) средней температуре теплоносителя, кото­рая называется номинальной средней температурой теплоносителя. Неболь­шой интервал температур, в пределах которого изменяется величина сред­ней температуры теплоносителя около номинального значения, называется зоной рабочих средних температур. Интервал температур от 20^оС до наи­меньшего из значений рабочих температур называется зоной разогрева ре­актора. Таким образом, после пуска реактора на минимально-контролируе­мый уровень мощности (МКУМ), чтобы окончательно привести реактор в ра­бочее состояние (как говорят: ввести реактор в энергетический режим), его разогревают с ограниченной скоростью путём медленного подъёма мощ­ности до тех пор, пока средняя температура теплоносителя не достигнет своей номинальной величины. При дальнейшей работе средняя температура теплоносителя в стационарных режимах поддерживается постоянной в силу естественных теплообменных свойств активной зоны на постоянном уровне мощности реактора, а в переходных режимах - ещё и корректируется сред­ствами автоматики регулирования реактора. Однако, точно расчётное зна­чение номинальной средней температуры теплоносителя выдержать не полу­чается даже средствами автоматической коррекции; именно в переходных режимах работы реактора величина средней температуры теплоносителя ко­леблется в пределах нескольких градусов около номинального значения.

Разница наибольшего и наименьшего значений температур при этом и составля­ет упомянутую выше зону рабочих средних температур. Температурный эффект реактивности при номинальной средней темпе ратуре теплоносителя называется полным температурным эффектом реактивности реактора.

Величина полного температурного эффекта реактивности у реакторов может быть как положительной (кривая ТЭР 1 типа), так и отрицательной (кривые ТЭР 2-го и 3-го типов). Абсолютные величины полных ТЭР энерге­тических реакторов могут достигать 2 ¸ 3 %, а это, как предстоит убедить­ся далее, очень больщие реактивности, высвобождение которых может соз­дать ядерно-опасную ситуацию.

Температурным коэффициентом реактивности при данной средней температуре теплоносителя называется изменение реактивности реактора, вызванное его разогревом на 1^оС сверх этой температуры.
ТКР обозначается α_t(t_т), измеряется в 1/^оС или в %/^оС.

Обратим внимание, что кривые ТЭР в некоторых интервалах темпера­тур имеют восходящий характер, а в некоторых - падающий. Интенсивность возрастания или убывания величины ρ_t с ростом температуры не может нас не интересовать (и особенно - в зоне рабочих средних температур), т.к. это - реакция реактора на каждый градус изменения его температуры, которую для поддержания заданной мощности реактора оператор обязан скомпенсировать введением (или извлечением) в активную зону подвижных поглотителей.
Предположим, реактор разогревается от некоторой конкретной темпе­ратуры теплоносителя t_т на несколько градусов Δt_т, и при этом темпера­турное изменение реактивности составляет Δρ_t; отсюда следует, что сред­няя величина изменения температурного эффекта реактивности на 1^о этого интервала температур будет равна:

α_t = Δρ_t/Δt_т,

Но это - только средняя величина ежеградусного изменения темпера­турного эффекта реактивности в интервале температур от t_т до t_т+Δt_т, а при сужении интервала изменения температур Δt_т до элементарного (dt) в пределе получается локальное изменение температурного эффекта реактив­ности реактора при температуре t_т:

Это и есть локальная величина температурного коэффициента реактив­ности реактора при температуре t_т. Как видим, по отношению к функции температурного эффекта ρ_t(t_т) величина α_t - есть не что иное, как пер­вая производная функции температурного эффекта по средней температуре теплоносителя. Вот почему температурный коэффициент реактивности назы­вают дифференциальной мерой влияние температуры на реактивность реак­тора, в отличие от величины температурного эффекта реактивности:

который является интегральной мерой этого влияния.
Поскольку первая производная любой функции интерпретируется как тангенс угла наклона касательной к графику функции в данной точке, по­ложительный знак a_t при рассматриваемой температуре t_т свидетельствует, что функция температурного эффекта при этой температуре являются воз­растающей, а отрицательность a_t, напротив, означает, что функция тем­пературного эффекта при рассматриваемой температуре t_т убывает.
Форма кривых ТЭР 1 и 2-го типов, изображенных на рис.10.1, говорит о том, что в интервале температур от 20^оС до температуры, соответству­ющей максимуму кривой ТЭР, температурный коэффициент реактивности положителен, при температурах максимумумов - он равен нулю, а при более высоких температурах - отрицателен. Реактору с кривой ТЭР третьего ти­па отрицательный ТКР свойственен во всем диапазоне средних температур теплоносителя.
Оператору часто приходится решать задачи по оценке температурных изменений реактивности реактора при сравнительно небольших (в пределах <10^оС) изменений средней температуры теплоносителя (Δt_т). Кривой ТЭР в таких случаях пользоваться неудобно, поскольку она чаще всего вычерчи­вается в довольно крупном масштабе по оси температур (на одно деление приходится 5 ¸ 10^оС), и попытка снять малое изменение реактивности может обернуться большой относительной погрешностью из-за недостаточной ост­роты зрения и недостаточного качества исполнения графика ТЭР. В этом случае для нахождения Δρ_t пользуются тем, что в относительно небольшом интервале любая нелинейная зависимость мало отличается от линейной, и находят температурное изменение реактивности по формуле:

Δρ_t ≈ α_t(t_т) Δt_т (10.1.5)

Разумеется, для этого нужно знать величину α_t при температуре t_т. Поэтому для нахождения Δρ_t при небольшом (менее 10^оС) изменении средних температур теплоносителя в активной зоне (Δt_т) пользуются фор­мулой (10.1.5), а для более широких изменений температур теплоносителя (Δt_т>10^оС), в пределах которых нелинейностью функции ρ_t(t_т) пренебре­гать нельзя, - формулой (10.1.2).