Физические основы ядерной энергетики

Введение

ВВЭР (Водо-Водяной Энергетический Реактор) — водо-водяной корпусной энергетический ядерный реактор с водой под давлением, одна из наиболее удачных ветвей развития ядерных энергетических установок, получившая широкое распространение в мире.

ВВЭР был разработан в СССР параллельно с реактором РБМК и обязан своим происхождением одной из рассматривающихся в то время реакторных установок для атомных подводных лодок. Идея реактора была предложена в Курчатовском институте С. М. Фейнбергом. Работы над проектом начались в1954 году, в 1955 году ОКБ «Гидропресс» приступило к его разработке. Научное руководство осуществляли И. В. Курчатов и А. П. Александров.

Общее название реакторов этого типа в других странах — PWR, они являются основой мировой мирной ядерной энергетики. Первая станция с таким реактором была запущена в США в 1957 году, АЭС Шиппингпорт.

Первый советский ВВЭР (ВВЭР-210) был введен в эксплуатацию в 1964 году на первом энергоблоке Нововоронежской АЭС. Нововоронежская АЭС-2 - строящаяся станция неподалёку от Нововоронежской АЭС. Станция сооружается по новому проекту АЭС-2006, который предусматривает использование реакторов ВВЭР-1200, в настоящий момент ведётся сооружение 2-х энергоблоков общей мощностью 2400 МВт, в дальнейшем планируется построить ещё 2. Первоначально пуск первого энергоблока был запланирован на конец 2012 года, однако он был перенесён на 2014 год.

 

Физические основы ядерной энергетики

1.1. Цепная реакция деления ядер.

Рассмотрим механизм цепной реакции деления. При делении тяжелых ядер под действием нейтронов возникают новые нейтроны. Например, при каждом делении ядра урана ₉₂U²³⁵ в среднем возникает 2.4 нейтрона. Часть этих нейтронов снова может вызвать деление ядер. Такой лавинообразный процесс называется цепной реакцией.
Цепная реакция деления идет в среде, в которой происходит процесс размножения нейтронов. Такая среда называется активной зоной. Важнейшей физической величиной, характеризующей интенсивность размножения нейтронов, является коэффициент размножения нейтронов в среде k_∞. Коэффициент размножения равен отношению количества нейтронов в одном поколении к их количеству в предыдущем поколении. Индекс ∞ указывает, что речь идет об идеальной среде бесконечных размеров. Аналогично величине k_∞ определяется коэффициент размножения нейтронов в физической системе k. Коэффициент k является характеристикой конкретной установки.
В делящейся среде конечных размеров часть нейтронов будет уходить из активной зоны наружу. Поэтому коэффициент k зависит еще от вероятности Р для нейтрона не уйти из активной зоны. По определению

k = k∞P.

(1.1)

Величина Р зависит от состава активной зоны, ее размеров, формы, а также от того, в какой степени окружающее активную зону вещество отражает нейтроны.

С возможностью ухода нейтронов за пределы активной зоны связаны важные понятия критической массы и критических размеров. Критическим размером называется размер активной зоны, при котором k = 1. Критической массой называется масса активной зоны критических размеров. Очевидно, что при массе ниже критической цепная реакция не идет, даже если > 1. Наоборот, заметное превышение массы над критической ведет к неуправляемой реакции - взрыву.
Если в первом поколении имеется N нейтронов, то в n-м поколении их будет Nkⁿ. Поэтому при k = 1 цепная реакция идет стационарно, при k < 1 реакция гаснет, а при k > 1 интенсивность реакции нарастает. При k = 1 режим реакции называется критическим, при k > 1 – надкритическим и при k < 1 – подкритическим.
Время жизни одного поколения нейтронов сильно зависит от свойств среды и имеет порядок от 10^–4 до 10^–8 с. Из-за малости этого времени для осуществления управляемой цепной реакции надо с большой точностью поддерживать равенство k = 1, так как, скажем, при k = 1.01 система почти мгновенно взорвется. Посмотрим, какими факторами определяются коэффициенты k_∞ и k.
Первой величиной, определяющей k_∞(или k), является среднее число нейтронов, испускаемых в одном акте деления. Число зависит от вида горючего и от энергии падающего нейтрона. В табл. 1 приведены значения основных изотопов ядерной энергетики, как для тепловых, так и для быстрых (Е = 1 МэВ) нейтронов.

Рис.1. Энергетический спектр нейтронов, испущенных при делении тепловыми нейтронами ядра 235U

Энергетический спектр нейтронов деления для изотопа ²³⁵U приведен на рис. 1. Такого рода спектры сходны для всех делящихся изотопов: имеется сильный разброс по энергиям, причем основная масса нейтронов имеет энергии в области 1–3 МэВ. Возникшие при делении нейтроны замедляются, диффундируют на некоторое расстояние и поглощаются либо с делением, либо без него. В зависимости от свойств среды нейтроны успевают до поглощения замедлиться до различных энергий. При наличии хорошего замедлителя основная масса нейтронов успевает замедлиться до тепловых энергий порядка 0.025 эВ. В этом случае цепная реакция называется медленной, или, что то же самое, тепловой. При отсутствии специального замедлителя нейтроны успевают замедлиться лишь до энергий 0.1–0.4 МэВ, так как все делящиеся изотопы – тяжелые и поэтому замедляют плохо. Соответствующие цепные реакции называются быстрыми (подчеркнем, что эпитеты “быстрый” и “медленный” характеризуют скорость нейтронов, а не скорость реакции). Цепные реакции, в которых нейтроны замедляются до энергий от десятков до одного кэВ, называются промежуточными.
При столкновении нейтрона с тяжелым ядром всегда возможен радиационный захват нейтрона (n,γ). Этот процесс будет конкурировать с делением и тем самым уменьшать коэффициент размножения. Отсюда вытекает, что второй физической величиной, влияющей на коэффициенты k_∞, k, является вероятность деления при захвате нейтрона ядром делящегося изотопа. Эта вероятность для моноэнергетических нейтронов, очевидно, равна

,

(1.2)

где _nf, _nγ – соответственно сечения деления и радиационного захвата. Для одновременного учета как числа нейтронов на акт деления, так и вероятности радиационного захвата вводится коэффициентη, равный среднему числу вторичных нейтронов на один захват нейтрона делящимся ядром.

,

(1.3)

величина η зависит от вида горючего и от энергии нейтронов. Значения η для важнейших изотопов для тепловых и быстрых нейтронов приведены в той же табл. 1. Величина η является важнейшей характеристикой ядер горючего. Цепная реакция может идти только при η > 1. Качество горючего тем выше, чем больше значение η.

 

Таблица 1. Значения ν, η для делящихся изотопов

Ядро	92U233	92U235	94Pu239
Тепловые нейтроны (Е = 0.025 эВ)	ν	2.52	2.47	2.91
η	2.28	2.07	2.09
Быстрые нейтроны (E = 1 МэВ)	ν	2.7	2.65	3.0
η	2.45	2.3	2.7

Качество ядерного горючего определяется его доступностью и коэффициентом η. В природе встречаются только, три изотопа, которые могут служить ядерным топливом или сырьем для его получения. Это изотоп тория ²³²Th и изотопы урана ²³⁸U и ²³⁵U. Из них первые два цепной реакции не дают, но могут быть переработаны в изотопы, на которых реакция идет. Изотоп ²³⁵U сам дает цепную реакцию. В земной коре тория в несколько раз больше, чем урана. Природный торий практически состоит только из одного изотопа ²³²Th. Природный уран в основном состоит из изотопа²³⁸U и только на 0.7% из изотопа ²³⁵U.
На практике крайне важен вопрос об осуществимости цепной реакции на естественной смеси изотопов урана, в которой на одно ядро ²³⁵U приходится 140 ядер ²³⁸U. Покажем, что на естественной смеси медленная реакция возможна, а быстрая – нет. Для рассмотрения цепной реакции на естественной смеси удобно ввести новую величину – среднее сечение поглощения нейтрона, отнесенное к одному ядру изотопа ²³⁵U. По определению

.

(1.4)

где верхний индекс указывает массовое число соответствующего изотопа урана. Вероятность того, что нейтрон, поглотившись в естественной смеси, вызовет деление, равна

.

Умножив эту вероятность на число ν нейтронов, вылетающих в среднем при делении одного ядра, мы получим по аналогии с (3) коэффициент η^ест для естественной смеси:

.

(1.5)

Для тепловых нейтронов = 2.47, = 580 барн, = 112 барн, = 2.8 барн (обратите внимание на малость последнего сечения). Подставив эти цифры в (5), мы получим, что для медленных нейтронов в естественной смеси

ест(медл.) = 1.32 > 1.

(1.6)

Это означает, что 100 тепловых нейтронов, поглотившись в естественной смеси, создадут 132 новых нейтрона. Отсюда прямо следует, что цепная реакция на медленных нейтронах в принципе возможна на естественном уране. В принципе, потому что для реального осуществления цепной реакции надо уметь замедлять нейтроны с малыми потерями.
Для быстрых нейтронов ν = 2.65, 2 барн, 0.1 барн. Если учитывать деление только на изотопе ²³⁵U, получим

235(быстр.) 0.3.

(1.7)

Но надо еще учесть, что быстрые нейтроны с энергиями больше 1 МэВ могут с заметной относительной интенсивностью делить и ядра изотопа ²³⁸U, которого в естественной смеси очень много.

Для деления на ²³⁸U коэффициент равен примерно 2.5. В спектре деления примерно 60% нейтронов имеют энергии выше эффективного порога 1.4 МэВ деления на ²³⁸U. Но из этих 60% только один нейтрон из 5 успевает произвести деление, не замедлившись до энергии ниже пороговой за счет упругого и особенно неупругого рассеяния. Отсюда для коэффициента ²³⁸(быстр.) получается оценка

η238(быстр.) = 0.6ν238/5 ≈ 0.3.

(1.8)

Полный коэффициент η^ест для быстрой реакции равен сумме:

ηест(быстр.) = η235(быстр.) + η238(быстр.) ≈ 0.6 < 1.

(1.9)

Таким образом, на быстрых нейтронах цепная реакция в естественной смеси (²³⁵U + ²³⁸U) идти не может. Экспериментально установлено, что для чистого металлического урана коэффициент размножения достигает значения единицы при обогащении 5.56%. Практически оказывается, что реакцию на быстрых нейтронах можно поддерживать лишь в обогащенной смеси, содержащей не меньше 15% изотопа ²³⁵U.

Естественную смесь изотопов урана можно обогащать изотопом ²³⁵U. Обогащение является сложным и дорогостоящим процессом из-за того, что химические свойства обоих изотопов почти одинаковы. Приходится пользоваться небольшими различиями в скоростях химических реакций, диффузии и др., возникающими вследствие различия масс изотопов. Цепную реакцию на ²³⁵U практически всегда осуществляют в среде с большим содержанием ²³⁸U. Часто используется естественная смесь изотопов, для которой η = 1.32 в области тепловых нейтронов, так как ²³⁸U также полезен. Изотоп ²³⁸U делится нейтронами с энергией выше 1 МэВ. Это деление приводит к небольшому дополнительному размножению нейтронов.
Сравним цепные реакции деления на тепловых и быстрых нейтронах.
У тепловых нейтронов сечения захвата велики и сильно меняются при переходе от одного ядра к другому. На ядрах некоторых элементов (например, на кадмии) эти сечения в сотни и более раз превосходят сечения на ²³⁵U. Поэтому к активной зоне установок на тепловых нейтронах предъявляются требования высокой чистоты по отношению к некоторым примесям.
Для быстрых нейтронов все сечения захвата малы и не так уж сильно отличаются друг от друга, так что проблемы высокой чистоты материалов не возникает. Другим преимуществом быстрых реакций является более высокий коэффициент воспроизводства.
Важное отличительное свойство тепловых реакций состоит в том, что в активной зоне топливо значительно сильнее разбавлено, т. е. на одно ядро топлива приходится значительно больше не участвующих в делении ядер, чем в быстрой реакции. Например, в тепловой реакции на естественном уране на ядро топлива ²³⁵U приходится 140 ядер сырья ²³⁸U, а в быстрой реакции на ядро ²³⁵U может приходиться не более пяти-шести ядер ²³⁸U. Разбавленность топлива в тепловой реакции приводит к тому, что одна и та же энергия в тепловой реакции выделяется в значительно большем объеме вещества, чем в быстрой. Тем самым из активной зоны тепловой реакции легче отводить тепло, что позволяет осуществлять эту реакцию с большей интенсивностью, чем быструю.
Время жизни одного поколения нейтронов для быстрой реакции на несколько порядков меньше, чем для тепловой. Поэтому скорость протекания быстрой реакции может заметно измениться через очень короткое время после изменения физических условий в активной зоне. При нормальной работе реактора этот эффект несуществен, поскольку в этом случае режим работы определяется временами жизни запаздывающих, а не мгновенных нейтронов.
В однородной среде, состоящей только из делящихся изотопов одного вида, коэффициент размножения был бы равен η. Однако в реальных ситуациях, кроме делящихся ядер, всегда присутствуют другие, неделящиеся. Эти посторонние ядра будут захватывать нейтроны и тем самым влиять на коэффициент размножения. Отсюда следует, что третьей величиной, определяющей коэффициенты k_∞, k, является вероятность того, что нейтрон не будет захвачен одним из неделящихся ядер. В реальных установках “посторонний” захват идет на ядрах замедлителя, на ядрах различных конструктивных элементов, а также на ядрах продуктов деления и продуктов захвата.
Для осуществления цепной реакции на медленных нейтронах в активную зону вводят специальные вещества – замедлители, которые превращают нейтроны деления в тепловые. На практике цепная реакция на медленных нейтронах осуществляется на естественном или слегка обогащенном изотопом²³⁵U уране. Присутствие большого количества изотопа ²³⁸U в активной зоне усложняет процесс замедления и делает необходимым предъявление высоких требований к качеству замедлителя. Жизнь одного поколения нейтронов в активной зоне с замедлителем приближенно можно разбить на две стадии: замедление до тепловых энергий и диффузия с. тепловыми скоростями до поглощения. Для того чтобы основная часть нейтронов успела замедлиться без поглощения, необходимо выполнение условия

σупр/σзахв >> n,

(1.10)

Рис. 2. Сечение радиационного захвата нейтронов ядрами изотопа урана 238U в резонансной области энергий

где σ_упр, σ_захв – усредненные по энергиям сечения соответственно упругого рассеяния и захвата, а n – число столкновений нейтрона с ядрами замедлителя, необходимое для достижения тепловой энергии. Число n быстро растет с ростом массового числа замедлителя. Для урана ²³⁸U число n имеет порядок нескольких тысяч. А отношение σ_упр/σ_захв для этого изотопа даже в сравнительно благоприятной области энергий быстрых нейтронов не превышает 50. Особенно же “опасна” в отношении захвата нейтронов так называемая резонансная область от 1 кэВ до 1 эВ. В этой области полное сечение взаимодействия нейтрона с ядрами ²³⁸U имеет большое число интенсивных резонансов (рис. 2). При низких энергиях радиационные ширины превышают нейтронные. Поэтому в области резонансов отношение σ_упр/σ_захв становится даже меньше единицы. Это означает, что при попадании в область одного из резонансов нейтрон поглощается практически со стопроцентной вероятностью. А так как замедление на таком тяжелей ядре, как уран, идет “мелкими шагами”, то при прохождении через резонансную область замедляющийся нейтрон обязательно “наткнется” на один из резонансов и поглотится. Отсюда следует, что на естественном уране без посторонних примесей цепную реакцию осуществить нельзя: на быстрых нейтронах реакция не идет из-за малости коэффициента η, а медленные нейтроны не могут образоваться, Для того чтобы избежать резонансного захвата нейтрона, надо использовать для замедления очень легкие ядра, на которых замедление идет “крупными шагами”, что резко увеличивает вероятность благополучного “проскакивания” нейтрона через резонансную область энергий. Наилучшими элементами-замедлителями являются водород, дейтерий, бериллий, углерод. Поэтому используемые на практике замедлители в основном сводятся к тяжелой воде, бериллию, окиси бериллия, графиту, а также обычной воде, которая замедляет нейтроны не хуже тяжелой воды, но поглощает их в гораздо большем количестве. Замедлитель должен быть хорошо очищен. Заметим, что для осуществления медленной реакции замедлителя должно быть в десятки, а то и в сотни раз больше, чем урана, чтобы предотвратить резонансные столкновения нейтронов с ядрами ²³⁸U.

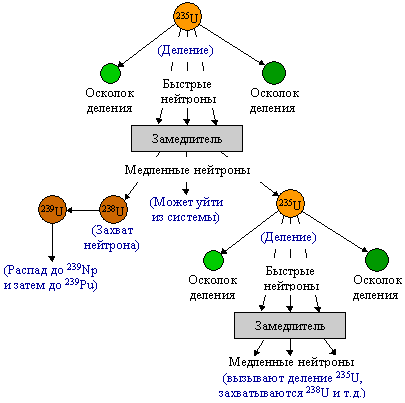Рис. 3. Схема цепной реакции в среде с замедлителем

 

Замедляющие свойства активной среды приближенно могут быть описаны тремя величинами: вероятностью нейтрону избежать поглощения замедлителем во время замедления, вероятностью р избежать резонансного захвата ядрами ²³⁸U и вероятностью f тепловому нейтрону поглотиться ядром горючего, а не замедлителя. Величина f называется обычно коэффициентом теплового использования. Точный расчет этих величин сложен. Обычно для их вычисления пользуются приближенными полуэмпирическими формулами.

Величины p и f зависят не только от относительного количества замедлителя, но и от геометрии его размещения в активной зоне. Активная зона, состоящая из однородной смеси урана и замедлителя, называется гомогенной, а система их чередующихся блоков урана и замедлителя называется гетерогенной. Качественно гетерогенная система отличается тем, что в ней образовавшийся в уране быстрый нейтрон успевает уйти в замедлитель, не достигнув резонансных энергий. Дальнейшее замедление идет уже в чистом замедлителе. Это повышает вероятность p избежать резонансного захвата

p_гет > p_гом.

С другой стороны, наоборот, став в замедлителе тепловым, нейтрон должен для участия в цепной реакции продиффундировать, не поглотившись в чистом замедлителе, до его границы. Поэтому коэффициент теплового использования f в гетерогенной среде ниже, чем в гомогенной:

f_гет < f_гом.

Для оценки коэффициента размножения k_∞ теплового реактора используется приближенная формула четырех сомножителей

k∞ = ηpfε.

(1.11)

Первые три сомножителя мы уже рассматривали ранее. Величина ε называется коэффициентом размножения на быстрых нейтронах. Этот коэффициент вводится для того, чтобы учесть, что часть быстрых нейтронов может произвести деление, не успев замедлиться. По своему смыслу коэффициент ε всегда превышает единицу. Но это превышение обычно невелико. Типичным для тепловых реакций является значение ε = 1.03. Для быстрых реакций формула четырех сомножителей неприменима, так как каждый коэффициент зависит от энергии и разброс по энергиям при быстрых реакциях очень велик.
Поскольку величина η определяется видом топлива, а величина ε для медленных реакций почти не отличается от единицы, то качество конкретной активной среды определяется произведением pf. Так, преимущество гетерогенной среды перед гомогенной количественно проявляется в том, что, например, в системе, в которой на одно ядро естественного урана приходится 215 ядер графита, произведение pf равно 0,823 для гетерогенной среды и 0,595 для гомогенной. А так как для естественной смеси η = 1,34, то мы и получим, что для гетерогенной среды k_∞ > 1, а для гомогенной k_∞ < 1.
Для практического осуществления стационарно текущей цепной реакции надо уметь этой реакцией управлять. Это управление существенно упрощается благодаря вылету запаздывающих нейтронов при делении. Подавляющее большинство нейтронов вылетает из ядра практически мгновенно (т. е. за время, на много порядков меньшее времени жизни поколения нейтронов в активной зоне), но несколько десятых процента нейтронов являются запаздывающими и вылетают из ядер-осколков через довольно большой промежуток времени – от долей секунды до нескольких и даже десятков секунд. Качественно влияние запаздывающих нейтронов можно пояснить так. Пусть коэффициент размножения мгновенно возрос от подкритического значения до такого надкритического, что k < 1 при отсутствии запаздывающих нейтронов. Тогда, очевидно, цепная реакция начнется не сразу, а лишь после вылета запаздывающих нейтронов. Тем самым процесс течения реакции будет регулируемым, если время срабатывания регулирующих устройств будет меньше сравнительно большого времени задержки запаздывающих нейтронов, а не очень малого времени развития цепной реакции. Доля запаздывающих нейтронов в ядерных горючих колеблется от 0.2 до 0.7%. Среднее время жизни запаздывающих нейтронов составляет приблизительно 10 с. При небольшой степени надкритичности скорость нарастания интенсивности цепной реакции определяется только запаздывающими нейтронами.
Захват нейтронов не участвующими в цепной реакции ядрами снижает интенсивность реакции, но может быть полезным в отношении образования новых делящихся изотопов. Так, при поглощении нейтронов изотопов урана ²³⁸U и тория ²³²Th образуются (через два последовательных b-распада) изотопы плутония ²³⁹Pu и урана ²³³U, являющиеся ядерным горючим:

,

(1.12)

 

.

(1.13)

Эти две реакции открывают реальную возможность воспроизводства ядерного горючего в процессе течения цепной реакции. В идеальном случае, т. е. при отсутствии ненужных потерь нейтронов, на воспроизводство может идти в среднем – 1 нейтронов на каждый акт поглощения нейтрона ядром горючего.

1.2 Зависимость эффективного коэффициента размножения от обогащения ядерного топлива.

На рис. 2.3 показана зависимость k_∞ от обогащения (2.11). Видно, что при увеличении e5 от 0,712% до 5% значение k_∞ возрастает от 1,0 до 1,42, хотя темп роста постепенно падает.

Рис.2.3 Зависимость эффективного коэффициента размножения от обогащения ядерного топлива

Условия критичности реактора.

Итак, выше были определены способы оценки коэффициентов размножения для бесконечной среды k_∞, теперь необходимо связать свойства реального реактора конечных размеров и состава среды и указать условия критичности для него.

Для этого для реактора на тепловых нейтронах в модели диффузии необходимо ввести ряд понятий.

Материальный параметр реактора c2м определяется как величина:

c2м =1/L2*(nfSf /Sа –1) (2.13)

Геометрический параметр реактора В20 (или баклинг) в наиболее распространенном случае цилиндрического реактора определяется как:

В20=(2.405/R)2+(p/H)2 (2.14)

Где: R – радиус, а Н – высота реактора, соответственно.

Следует отметить, что в состав c2м входят только характеристики материального состава реактора (диффузионные, поглощающие и т.п.). В состав В20 входят напротив только характеристики размеров реактора.

Условие критичности реактора без отражателя формулируется следующим образом: «Необходимым и достаточным условием критичности для реактора без отражателя (только для тепловых нейтронов в диффузионном приближении) является равенство материального и геометрического параметров» т.е.:

c2м = В20. (2.15а)

Другой формой этого же условия является уже известное нам соотношение:

Kэфф = k_∞ *Р (2.15в)

Где Р- вероятность избежать утечки в диффузионном приближении. Эта вероятность может быть записана как:

Р=1/(1+ L2 *В02)

Тогда выражение для Kэфф приобретает самый известный вид:

Kэфф = k_∞ */(1+ L2 *В02) (2.15с)

Практическая важность этих условий состоит в том, что они указывают пути вывода реактора в критическое состояние. В соответствии с (2.15а) реактор можно вывести в критическое состояние (а потом удерживать в нем) только двумя путями:

При фиксированном составе среды (обогащении топлива и поглощении) реактор можно сделать критическим путем изменения размера размножающей среды (т.е. В02). Это можно реализовать догрузкой топливных кассет, изменением уровня воды в решетке топливных элементов и т.п.

При фиксированном размере реактор можно вывести в критическое состояние (а потом удерживать в нем) изменением состава среды – т.е. загрузкой свежего топлива и выгрузкой выгоревшего (изменение обогащение топлива) или введением/извлечением поглотителей (т.е. изменением c2м).

Реально можно использовать оба пути, но в реакторах ВВЭР изменение поглощения обычно регулируется с помощью борной кислоты или стержней системы управления, а изменение свойств деления –загрузкой свежего топлива. Указанные соотношения получены аналитически, но в них учтены вклады только тепловых диффундирующих нейтронов.

Если в рассмотрении учесть также замедляющиеся нейтроны, то оценки будут точнее. Для замедляющихся нейтронов вводится понятие «возраст нейтронов»:

t(u)= (2.16)

где u- летаргия нейтронов (u=ln(2МэВ/Е)). Вводится характеристика, объединяющая характеристики замедления и диффузии, называемая «площадью миграции» - М2= L2 +t.

Тогда более точной и наиболее употребляемой оценкой для Кэф, аналогичной (2.15c), будет:

Кэфф = k_∞ */(1+ М2 *В02) (2.15d)

Наконец, последнее уточнение этих соотношений необходимо, если в реакторе используется отражатель толщиной D. Тогда в геометрическом параметре вместо радиуса R и высоты реактора Н используется (R+d) и (Н+d), где d -т.н. эффективная добавка отражателя d. Реакторы на ториевом топливном цикле подобны реакторам на быстрых нейтронах. В реакторах этого типа естественный торий-232 при поглощении нейтронов превращается в делящийся изотоп урана (уран-233). Этот изотоп, участвуя в цепной реакции деления, выделяет теплоту и избыточные нейтроны, которые преобразовывают еще большее количество тория в U-233. Такая технология привлекательна тем, что, во-первых, позволяет избежать производства плутония, во-вторых, в качестве топлива используется довольно распространенный торий, а, в-третьих, эффективность использования топлива может быть близка к эффективности реакторов на быстрых нейтронах.

1.3 Характеристики поля нейтронов

Плотность нейтронов

Плотность нейтронов (n) - это число нейтронов, находящихся в данный момент времени в единичном объёмесреды.
Из определения следует, что размерность плотности нейтронов - нейтр./см³, или, более формально - см^-3.
Плотность нейтронов является сугубо статической характеристикой: в определении нет и намёка на то, что нейтроны движутся; в нём внима­ние сосредоточено только на факте присутствия в данный момент времени в единичном объёме среды определённого числа нейтронов и не дает представления ни о характере, ни о нап­равлении, ни о скорости их движения. Это определение не даёт представ­ления о том, равномерно или неравномерно размещены эти нейтроны в этом объёме. Для математического описания больших количеств нейтронов в больших объёмах среды с помощью непрерывных функций необходимо иметь строгое определение, охватывающее понятие и локальной плотности нейтронов.
Вот почему Ядерный Стандарт рекомендует более общее определение:
Плотность нейтронов - это отношение числа нейтронов, находящихся в данный момент времени в объёме элементарной сферы, к величине объёма этой сферы.
Элементарный объём - это объём, величина которого может быть сколь угодно малой, поэтому (в соответствии с понятием математики) оправдан­ным является его обозначение как dV. Значит, если в объёме dV в данный момент времени содержится dN нейтронов, то локальная плотность нейтро­нов в этом элементарном объёме (практически - "в точке", т.к. в преде­ле элементарный объём стягивается в точку) будет:

n = dN/dV. (2.3.1)

Стандартное определение плотности нейтронов является величиной непрерывной, меняющей­ся в объёме среды плавно, "от точки к точке", допуская при этом, что n может принимать не только целые значения, но и дробно-долевые, например, n = 0.0784 нейтр/см³ или n = 3.496 нейтр/см³.

 

А это удобно тем, что для математического описания нейтронных по­лей становится возможным использовать компактный аналитический аппарат непрерывных функций, который во всех отношениях удобнее дискретных описаний.

1.3.2. Скорость движения нейтронов (v) или их кинетическая энер­гия (Е).

В ядерном реакторе функционируют свободные нейтроны широкого диапазона кинетических энергий - от 10^-3 эВ до десятков МэВ. Для удобс­тва их различий они классифицируются на:
- быстрые нейтроны (с кинетическими энергиями выше 0.1 МэВ);
- промежуточные нейтроны ( с энергиями 0.625эВ < E < 0.1МэВ);
- медленные нейтроны ( с энергиями ниже 0.625 эВ).
Необходимость такой классификации обусловлена тем, что нейтроны различных кинетических энергий обладают различной с клонностью к вступ­лению в одни и те же нейтронные реакции с ядрами одних веществ.
Особую часть медленных нейтронов составляют тепловые нейтроны - то есть нейтроны, находящиеся в кинетическом равновесии с ядрами среды, в которой они движутся. Поскольку энергетическое распределение молекул (а следовательно, и атомов, и ядер атомов) в их тепловом движении имеет вид спектра Л.Больцмана:

N(E) = N _о ^.C ^.E exp(-E / kT),

- аналогичное распределение должны иметь в непоглощающей среде и тепловые нейтроны: раз они находятся в кинетическом равновесии с ядра­ми атомов среды, то каждой группе ядер, имеющих определенную энергию Е, должна соответствовать пропорциональная по численности группа нейтро­нов той же энергии. Поэтому энергетический спектр тепловых нейтронов – спектр Максвелла - в непоглощающих средах формально описы­вается тем же выражением:

n(E) = n_o C E exp(-E / kT) (2.3.3)

где: n(E) - плотность тепловых нейтронов, имеющих энергии в элементар­ном интервале dE вблизи значения Е;
n_o - интегральная плотность тепловых нейтронов всех возможных энергий в среде с термодинамической температурой Т;
k = 8.62 ^.10^-5 эВ/К - постоянная Больцмана;
С - постоянный сомножитель нормировки.
В реальной (поглощающей нейтроны) среде максвелловское распреде­ление тепловых нейтронов по энергиям, конечно, нарушается. Однако, ком­пактное математическое удобство этого выражения настолько велико, что условились считать, что и в поглощающей тепловые нейтроны среде энер­гетическое распределение тепловых нейтронов сохраняет ту же (гауссову) форму, что и в непоглощающей среде:

n(E) = n_o C E exp(-E / kT_н), (2.3.4)

с той лишь разницей, что в показателе экспоненциала стоит не термодинамическая температура среды Т, а так называемая темпера­тура нейтронов Т_н.
Максвелловский спектр тепловых нейтронов (рис.2.9) характеризует­ся следующими присущими ему энергиями тепловых нейтронов:
а )Наиболее вероятной энергией Е_нв = kT_н, соответствующей макси­муму распределения тепловых нейтронов по энергиям при данной темпе­ратуре нейтронов Т_н. Это означает, что тепловых нейтронов с кинетичес­кой энергией Е_нв в среде больше, чем тепловых нейтронов любых других энергий (до 36% от общего числа всех тепловых нейтронов).
б) Средней энергией тепловых нейтронов:

Е_ср = (1/n_o) ∫₀^∞E n(E) dE (2.3.5)

Подстановка в (2.3.5) выражения (2.3.4) приводит к величине:

E_ср = 4kT_н / p ≈ 1.273 kT_н = 1.273 Е_нв (2.3.6)

В частности при температуре нейтронов Т_н = 293К (или 20^оС), называемой стандартной температурой, наиболее вероятная и средняя энергии тепло­вых нейтронов соответственно равны:
E_нв = 0.0253 эВ

Е_ср = 0.0322 эВ
Важным свойством максвелловского спектра является:
Отношение средней и наиболее вероятной энергий нейтронов в спектре Максвелла при постоянной температуре нейтронов есть величина постоянная, равная Е_ср/Е_нв= 4/ π ≈ 1.273.
Таким образом, отношение скоростей нейтронов, соответствующих средней и наиболее вероятной энергиям тепловых нейтронов:

v_ср/v_нв = √4/ π = 2/ √π ≈ 1.128, (2.3.7)

- то есть также является постоянной величиной. Понятие средней энергии тепловых нейтронов нужно для того, чтобы поведение и взаимодействия всей совокупности различных по энергиям тепловых нейтронов заменить эквивалентным их взаимодействием с ядрами среды так, словно все они одинаковы по энергиям, а значит - и по своим свойствам. Суммирование кинетической энергии всех тепловых нейтронов и раздел этой суммы поровну между всеми тепловыми нейтронами - см. формулу (2.3.5) - как раз и приводит к понятию "среднего теплово­го нейтрона", подобно понятию «среднего нейтрона деления». Спектр нейтронов, то есть их энергетическое распределение в среде, является второй характеристикой нейтронного поля.
К сожалению, теория реакторов до сих пор не располагает компакт­ным аналитическим выражением для спектра всех нейтронов в реакторе, и поэтому задачу по выяснению реакторного спектра приходится решать путём громоздких вычислений с помощью ЭВМ. Частные же задачи теории решаются на базе трёх энергетических спектров: спектр нейтронов деления (Уатта); спектр тепловых нейтронов (Максвелла) и спектр замедляющихся нейтронов (Ферми), с которым мы познакомимся позже.