Если прямая линия лежит на поверхности, то она — геодезическая линия этой поверхности. Действительно, кривизна прямой γ тождественно равна нулю. Поэтому в каждой точке P∈γ вектор кривизны k  , а, следовательно, и его ортогональная проекция
, а, следовательно, и его ортогональная проекция  g на касательную плоскость TPΠ равны нулю, откуда kg≡0. Таким образом, прямолинейные образующие однополостного гиперболоида, эллиптического параболоида, конуса с выколотой вершиной и цилиндра являются примерами геодезических линий на этих поверхностях.
g на касательную плоскость TPΠ равны нулю, откуда kg≡0. Таким образом, прямолинейные образующие однополостного гиперболоида, эллиптического параболоида, конуса с выколотой вершиной и цилиндра являются примерами геодезических линий на этих поверхностях.
Теперь докажем, что геодезическими линиями на плоскости являются прямые и только они.
Первый способ. Как сказано выше, любая прямая, лежащая на поверхности, является геодезической линией. Поскольку через любую точку P плоскости в данном направлении можно провести прямую, и она — геодезическая, то в силу единственности непараметризованной геодезической линии, проходящей через данную точку в данном направлении (теорема 3), других геодезических на плоскости нет.
Второй способ. Пусть Π— плоскость в E3. Тогда, в силу замечания можно выбрать прямоугольную систему координат Oxyz в E3 так, чтобы плоскость Oxy совпадала с плоскостью Π.
Замечание
В силу того, что кривая γ на поверхности Π является геодезической линией тогда и только тогда, когда ее касательные векторы образуют поле параллельного переноса вдоль γ, и того, что свойство гладкого векторного поля  (t)быть параллельным вдоль кривой σ на гладкой поверхности Π не зависит как от выбора параметризации поверхности, так и от параметризации кривой, то свойство гладких кривых γ на поверхности Π быть геодезическими линиями не зависит от параметризации поверхности.
(t)быть параллельным вдоль кривой σ на гладкой поверхности Π не зависит как от выбора параметризации поверхности, так и от параметризации кривой, то свойство гладких кривых γ на поверхности Π быть геодезическими линиями не зависит от параметризации поверхности.
Тогда Π задана уравнением z=0 или вектор-функцией 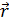 (x, y) ={x, y, 0}, где x, y - любые действительные числа. Откуда
(x, y) ={x, y, 0}, где x, y - любые действительные числа. Откуда 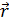 1=
1= 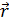 x={1,0,0},
x={1,0,0}, 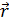 2=
2= 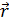 y={0,1,0} и (gij) =
y={0,1,0} и (gij) =  . Так как каждый элемент gij не зависит от x и y, то
. Так как каждый элемент gij не зависит от x и y, то  ≡0, поэтому система дифференциальных уравнений геодезических линий на плоскости Π имеет вид
≡0, поэтому система дифференциальных уравнений геодезических линий на плоскости Π имеет вид 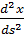 =0,
=0,  =0. Решения этой системы x(s)=c1s+c2, y(s)=c3s+c4, где c1, c2, c3, c4— произвольные константы, представляют собой все прямые на плоскости Π.
=0. Решения этой системы x(s)=c1s+c2, y(s)=c3s+c4, где c1, c2, c3, c4— произвольные константы, представляют собой все прямые на плоскости Π.
Геодезические на прямом геликоиде
Напомним, что, если прямая линия лежит на поверхности, то она — геодезическая линия этой поверхности. Действительно, кривизна прямой γ тождественно равна нулю. Поэтому в каждой точке P∈γ вектор кривизны k  , а, следовательно, и его ортогональная проекция
, а, следовательно, и его ортогональная проекция  gна касательную плоскость TPΠ равны нулю, откуда kg≡0. Таким образом, прямолинейные образующие однополостного гиперболоида, эллиптического параболоида, конуса с выколотой вершиной и цилиндра являются примерами геодезических линий на этих поверхностях.
gна касательную плоскость TPΠ равны нулю, откуда kg≡0. Таким образом, прямолинейные образующие однополостного гиперболоида, эллиптического параболоида, конуса с выколотой вершиной и цилиндра являются примерами геодезических линий на этих поверхностях.
Найти геодезические линии на прямом геликоиде 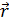 (u, v)={u*cosv, u*sinv, h*v}.
(u, v)={u*cosv, u*sinv, h*v}.
Решение:
Вычислим матрицу (gij) первой квадратичной формы поверхности и обратную к ней (gij):
(gij)= 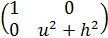 ; (gij)=
; (gij)=  .
.
Находим символы Кристоффеля второго рода
( ) =
) =  ; (
; (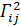 ) =
) =  .
.
Координатные линии v= const представляют собой прямые и как уточнено выше, являются геодезическими линиями прямого геликоида. Дифференциальное уравнение
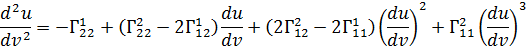
запишется в виде:
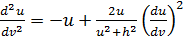 . (1)
. (1)
Сделаем замену:
p=  ,считаяp=p(u),
,считаяp=p(u),
при этом  и уравнение (1) примет вид:
и уравнение (1) примет вид:
 . (2)
. (2)
Положимq=p2,тогда 
из (2) имеем  (3)
(3)
Решаем соответствующее однородное уравнение:
 ,откуда
,откуда  и ln|q|=2ln(u2+h2)+lnc1.
и ln|q|=2ln(u2+h2)+lnc1.
Запишем общее решение однородного уравненияq=c1(u2+h2)2.В качестве частного решения неоднородного уравнения (3) возьмемq=−(u2+h2).Тогдаq=c1(u2+h2)2−(u2+h2)— общее решение уравнения (3). Возвращаясь к переменнымu, v, мы получаем:
 .
.
Следовательно,
 ,
,
где c1иc2— произвольные константы, причем  .
.
Ответ:v=c0=constиv=F(u, c1,c2),  ,— множество геодезических линий прямого геликоида.
,— множество геодезических линий прямого геликоида.
Замечание
Для простоты все отображения, кривые и поверхности предполагаются требуемого класса гладкости.
Напомним, что гладкая кривая ρ=ρ(t), при t∈(α, β), называетсярегулярной,если ρ=0,∀t∈(α, β). Далее все кривые предполагаются регулярными. Все индексы, обозначенные малыми латинскими буквами i, j, k, l, s, mпринимают значения1 и 2, если не оговорено противное. Так же будут использовать тензорные обозначения.
Литература
1. Геодезические линии. Степанов С. Е. 2000г. МАТЕМАТИКА
2. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ НА ПОВЕРХНОСТЯХ. Составители:Жукова Н.И., Багаев А.В. Учебно-методическое пособие. — Н. Новгород:Издательство Нижегородского госуниверситета. — 2008. – 54 с.
3. Картан Э. Внешние дифференциальные системы и их геометрические приложения. М.: Изд-во МГУ, 1962
4. Рашевский П.К. Курс дифференциальной геометрии (3-е изд.). М.-Л.: ГИТТЛ, 1950