4.1. Проектирование прямозубой эвольвентой передачи
Для проектирования заданными являются числа зубьев колес z1 = 15,
z2 = 32 и модуль m = 4,0 мм. Так как, z1 < zmin = 17, шестерню необходимо нарезать со смещением инструмента, чтобы обеспечить приемлемые эксплуатационные характеристики передачи.
По блокирующему контуру [3] для передачи, составленной из зубчатых колес с заданными числами зубьев, определяем коэффициенты смещения
x1 = 0,46, x2 = 0,25
4.1.1. Геометрический расчет передачи
Выполняем геометрический расчет передачи по методике, изложенной в [4]. Определяем коэффициент суммы смещений
ХΣ = х1 + х2 = 0,46 + 0,25= 0,71
и определяем угол зацепления αw
inv αw = (2 · ХΣ · tgα)/(z1 + z2) + invα;
inv αw = (2 · 0,71 · tg20˚)/(15 + 32) + inv20˚ = 0,025901
Значение αw определяем по значению эвольвентой функции из таблиц:
αw = 23,8695˚
Делительное межосевое расстояние
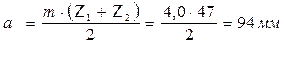
Межосевое расстояние
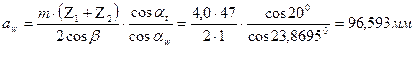
Рассчитываем диаметры зубчатых колес.
Делительные диаметры
d1 = m · z1 = 4,0 · 15 = 60 мм
d2 = m · z2 = 4,0 · 32 = 128 мм
Передаточное число
u12 = z2 / z1 = 32/15 = 2,133
Начальные диаметры
dw1 = 2аw/(u + 1) = 2 · 96,593/(2,133 + 1) = 61,655 мм
dw2 =2аwu12/(u + 1) =2 · 96,593 · 2,133/(2,133 + 1) = 131,531 мм
Коэффициент воспринимаемого смещения
y = (аw - а)/m = (96,593 – 94)/4,0 = 0,648
Коэффициент уравнительного смещения
Δy = ХΣ - y = 0,71 – 0,648= 0,062
Диаметры вершин зубьев
da1 = d1 + 2m(hа* + х1 - Δy) = 60 + 2 · 4,0 · (1 + 0,46 - 0,062) = 71,185 мм
da2 = d2 + 2m(hа* + х2 - Δy) = 128 + 2 · 4,0 · (1 + 0,25 - 0,062) = 137,505 мм
Диаметры впадин зубьев (справочный размер)
df1 = d1 - 2m(hа* + c* - х1) = 60 – 2 · 4,0·(1 + 0,25 – 0,46) = 53,68 мм
df2 = d2 - 2m(hа* + c* - х2) = 128 – 2 · 4,0·(1 + 0,25 – 0,25) = 120 мм
Основные диаметры
db1 = d1cosα = 60 · cos20˚ = 56,382 мм
db2 = d2cosα = 128 · cos20˚ = 120,281 мм
Нормальная толщина (по дуге делительной окружности) определяется как
Sn1 = m(π/2 + 2х1tgα) = 4,0 · (π/2 + 2 · 0,46 · tg20˚) = 7,623 мм
Sn2 = m(π/2 + 2х2tgα) = 4,0 · (π/2 + 2 · 0,25 · tg20˚) = 7,011 мм
Для зубчатых колес с положительным смещением необходимо проверять условие отсутствия заострения зуба, т.е. условие Sa > 0,2m.
Толщина зуба по дуге окружности вершин корригированной шестерни 1 определяется по формуле
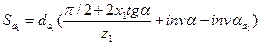
Sа1 = 71,185 · [(π/2 + 2 · 0,46 · tg20˚)/15 + inv20˚ - inv37,624˚] = 1,982 мм
где αа1 - угол профиля в точке на концентрической окружности диаметром dа1, рассчитывается как
соs αа1 = (d/dа1)cosα = (60/71,185)cos20˚ = 0,792;
αа1 = 37,624˚
Так как Sа1 = 1,982 мм > 0,2m = 0,2 · 4,0 = 0,8 мм,
то заострения корригированной шестерни 1 нет.
Толщина зуба по дуге окружности вершин корригированного колеса 2 определяется по формуле
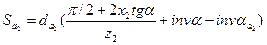

Sа2 = 137,505 · [(π/2 + 2 · 0,25 · tg20˚)/32 + inv20˚ - inv28,987˚] = 2,968 мм
где αа1 - угол профиля в точке на концентрической окружности диаметром dа1, рассчитывается как
соs αа2 = (d/dа2)cosα= (128/137,505)cos20˚ = 0,875;
αа2 = 28,987˚
Так как Sа2 = 2,968 мм > 0,2m = 0,2 · 4,0 = 0,8 мм,
то заострения корригированного колеса 2 нет.
Шаг зацепления по основной окружности (основной шаг) определяется
по зависимости
pα = π · m · cosα = π · 4,0 · cos20˚ = 11,809 мм
4.1.2. Построение картины зацепления
Проводим линию центров и в масштабе 0,00028 м/мм откладываем межосевое расстояние аw = 96,593 мм. Из центров вращения шестерни О1 и колеса О2 проводим окружности: начальные, основные, делительные, вершин и впадин зубьев.
Проводим общую касательную к основным окружностям - линию зацепления. Она проходит через точку касания начальных окружностей - полюс зацепления Р, что косвенно свидетельствует о правильности расчетов.
На основных окружностях строим эвольвенты. Для этого откладываем ряд одинаковых дуг и в точках деления проводим касательные. Вдоль касательных откладываем отрезки, равные длинам дуг разбиения. Полученные точки лежат на эвольвентах. Отложив по делительным окружностям нормальные толщины зубьев и отобразив симметрично эвольвенты, выстраиваем полный профиль зубьев. Выполняем шаблоны зубьев колес.
Строим картину пары зубьев, зацепляющихся в полюсе, а затем, откладывая по основным окружностям основной шаг, выстраиваем еще по паре зубьев.
Точки пересечения окружностей вершин с теоретической линией зацепления дают отрезок аb - рабочий участок линии зацепления.
4.1.3. Расчет эксплуатационных характеристик передачи
Коэффициент перекрытия определим по формуле
ε = ab/(π · m · cosα) = 15,96/(π · 4,0 · cos20˚) = 1,352,
где ab = 15,96 мм - длина рабочего участка линии зацепления с учетом масштаба построения.
Значение коэффициента торцового перекрытия показывает, что передача работает плавно (т.к. ε > 1,05).
Коэффициенты удельных скольжений рассчитываем по формулам
λ12 = 1 - (АВ - X)/(X·u12)
λ21 = 1 - (X·u12)/(АВ - X),
где АВ = 139,595 мм - длина теоретического участка линии зацепления без учета масштаба, Х - переменное расстояние от начала теоретического участка линии зацепления (точки А) до точки, в которой определяется коэффициент. Расчетные данные сводим в таблицу 4.1.
Таблица 4.1. Значения коэффициентов удельных скольжений
| Х, мм | 20,603 | 28,586 | 36,569 | АP=44,552 | 55,568 | 66,585 | 77,601 | 139,595 | |
| λ12 | - ∞ | -1,707 | -0,82 | -0,321 | 0,291 | 0,486 | 0,626 | ||
| λ21 | 0,631 | 0,451 | 0,243 | -0,411 | -0,946 | -1,67 | - ∞ |
По рассчитанным данным строим график удельных скольжений, приняв масштаб 0,025 1/мм.
4.2. Проектирование планетарного механизма
Для привода механизма выбираем двигатель с рабочей частотой вращения 8000 об/мин (ωдв = πn/30 = π · 8000/30 = 837,758 1/с). Привод, состоящий из открытой зубчатой передачи с заданными числами зубьев 15 и 32 и одноступенчатого планетарного редуктора, обеспечивает вращение входного кривошипа механизма с угловой скоростью 110 1/с.
Потребное передаточное число планетарного редуктора определим
iред = z1ωдв / (z2ω1) = (15 · 837,758)/(32 · 110) = 3,569
Выбираем схему планетарного редуктора и подбираем числа зубьев колес этого редуктора для обеспечения передаточного отношения iред= 3,569.
Принимаем z3 = 37 из условия подрезания зуба
Рассчитываем число зубьев опорного колеса 3
Z5 = (u3Н - 1) z3 = (3,569 - 1)37 = 95,09
Условие отсутствия заклинивания для внутреннего зацепления (z5>85),
Принимаем число z5 = 95 одинаковой чётности. Из условия соосности получаем: z4 = (z5 – z3)/2 = (95 - 37) / 2 = 29
Таким образом получаем z3 = 37, z4 = 29, z5 = 95
Из условия соседства число сателлитов не должно превышать К, где
К = 180˚/[arcsin((z4 + 2)/(z3 + z4))].
К=180˚/[arcsin((29 + 2)/(37 + 29))] = 6,425
Принимаем число сателлитов равным 6, т.е. К = 6, и проверяем условие сборки
С = (z3 + z5)/К = (37 + 95)/6 = 22
Поскольку С = 22 - целое число, то механизм может быть собран без натягов.
Проверяем условие обеспечения заданного передаточного отношения
U3Н = 1+ z5 /z3 = 1 + 95/37 = 3,568
Отклонение передаточного отношения составляет 0,068 %, что допустимо, поэтому принимаем z3 = 37, z4 = 29, z5 = 95.
Приняв модуль m = 4 мм, строим кинематическую схему планетарного редуктора на листе.
На схеме планетарного редуктора строим треугольник скоростей. По треугольнику скоростей определяем передаточное отношение редуктора.
Скорость точки А
VA = ωдв(mz3)/2 = 837,758 · (4 · 37)/2 = 61994,095 мм/с = 61,994095 м/с
На чертеже скорость т. А изображаем вектором длиной 100 мм. В полученном масштабе скорость точки В по треугольнику скоростей получаем в виде вектора длиной 50 мм. Тогда скорость точки В
VВ = (61,994095/100) · 50 = 30,997 м/с = 30997 мм/с,
а угловая скорость вала водила
ωН = VВ/(m(z3 + z4)/2) = 30997 /(4·(37 + 29)/2) = 234,826 1/с
Передаточное отношение редуктора по построению
iред = ωдв/ωН = 837,758/234,826= 3,567
Различие с аналитически определенным передаточным отношением составило 0,028 % что допустимо.
Вывод
В результате курсового проектирования был спроектирован механизм поперечно-строгального станка.
На первом этапе курсового проектирования я построил кинематическую схему в восьми положениях. Для каждого положения построил план скоростей и план ускорений. Также построили график зависимости угловых скоростей звеньев и линейных скоростей центров масс звеньев от угла поворота входного звена. Также построил график зависимости перемещения выходного звена от угла поворота входного звена. Дважды продифференцировал и получил график скоростей и ускорений выходного звена.
На втором листе был произведен кинетостатический расчет механизма и были определены реакции в кинематических парах и уравновешивающие силы. Определил уравновешивающую силу методом рычага Жуковского.
На третьем листе курсового проекта я определил приведенный момент инерции и приведенный момент сил сопротивления, построил диаграмму Виттенбауэра и определил размеры маховика.
На четвертом листе я построил картину зацепления зубчатых колес, рассчитал коэффициент удельного скольжения. Также подобрал количество чисел зубьев планетарного редуктора, для обеспечения заданного передаточного числа привода механизма поперечно-строгального станка.