Комплексная лабораторная работа № 7-8
Тема: Исследование цепи с емкостью. Исследование последовательной и параллельной RC цепи
Цель работы: Отработка практических навыков и проверка на опыте теоретических положений о распределении напряжений и фазовых сдвигов в электрической цепи при последовательном соединении RC- элементов
Часть лабораторной работы
Теоретическая часть.
Последовательное соединение RC элементов цепи
Реальный конденсатор характеризуется двумя параметрами: активным сопротивлением R и емкостным Хc (рисунок 1).

Рис.1 Электрическая цепь с резистивным и емкостным элементом
Полное напряжение цепи U определяется по теореме Пифагора из векторной диаграммы (рисунок 2).

Рис.2 Векторная диаграмма RC цепи
 U = √(UR)2 + (Uc)2, В
U = √(UR)2 + (Uc)2, В
где UR – напряжение на активном сопротивлении, В;
Uс - напряжение на емкостном сопротивлении, В
Действующее значение напряжения U
 |
I – ток цепи;
Z – полное сопротивление RC цепи из треугольника сопротивлений
 |
Z = √ R2 + (Xc)2, Ом
По закону Ома действующее значение тока в цепи:
I = U/Z, А
Сдвиг фаз:
 |
Пояснения к работе:
Студент при выполнении работы должен хорошо представлять, какие физические процессы происходят в электрической цепи.
Задание и исходные данные
1. 1. Приступая к выполнению данной лабораторной работы необходимо запустить программу ELECTRONICS WORKBENCH. После запуска она будет выглядеть следующим образом

1.2.Для работы необходимо построить или загрузить схему исследования.
При наличии загрузочного файла – после нажатия кнопки  открывается окно, в котором курсором необходимо пометить файл < Последовательное соединение RC .ewb > и нажать кнопку «Открыть». Появится схема, имеющая следующий вид:
открывается окно, в котором курсором необходимо пометить файл < Последовательное соединение RC .ewb > и нажать кнопку «Открыть». Появится схема, имеющая следующий вид:

3.Чтобы схема начала функционировать, необходимо нажать кнопку в верхнем правом углу.

Порядок выполнения работы
2.1. Опыт 1:Включить источник и произвести измерения в соответствии с ТАБЛИЦЕЙ. Выключить источник
2.2. Опыт 2:Изменить значения параметров схемы (в соответствии с таблицей) и провести исследование Результаты измерений занести в таблицу.
Провести расчет следующих величин
I = U/Z Xc = 1/ (ωC) Z=  cosj =
cosj = 
Полученные данные занести в таблицу
По опытным данным убедиться, что U = 
ТАБЛИЦА
| О П ЫТ | Измеренные величины | Расчетные величины | ||||||||
| С мкф | R кОм | U В | I мА | Uа В | Uс В | Xс | Z кОм | I мА | Cosj | |
| Опыт 1 | 0.0009 | 0.0009 | 133,3 | |||||||
| Опыт 2 | 4.6 | 7.5 | 0.0009 | 8,57 | 15,6 |
R– сопротивление резистора (резистор с переменным сопротивлением - реостат)
Обработка и анализ результатов
3.1. Данные измерений и расчетов внести в таблицу
3.2. Полученные данные занести в таблицу по опытным данным убедиться, что
U = 
3.3 Построить векторные диаграммы
Контрольные вопросы:
1. Как измениться угол сдвига фаз при уменьшении емкости конденсатора С?
Часть лабораторной работы
Теоретическая часть
Параллельное соединение RC
Параллельное соединение активного сопротивления, индуктивности и емкости.
Рассмотрим схему, состоящую из параллельно соединенных активного и реактивных элементов (рис.1, а).
Метод проводимостей и векторных диаграмм
Токи ветвей находятся сразу:  ,
,  ,
,  .
.
Для определения общего тока  необходимо построить векторную диаграмму (рис. 1, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем
необходимо построить векторную диаграмму (рис. 1, б). Построение начинаем с вектора напряжения, так как оно является общим для всех ветвей. Из векторной диаграммы имеем

или  ,
,
где  – полная проводимость цепи, равная
– полная проводимость цепи, равная
 .
.
Разность индуктивной и емкостной проводимостей представляет собой общую реактивную проводимость цепи  .
.

Рис. 2.31. Электрическая цепь и ее векторная диаграмма
Векторы токов на диаграмме образуют треугольник токов. Его горизонтальный катет, представляющий проекцию вектора тока на вектор напряжения, называется активной составляющей тока и равен току в активном элементе цепи:  (рис. 2, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов
(рис. 2, а). Проекция вектора тока на направление, перпендикулярное напряжению, – это реактивная составляющая тока. Она равна суммарному току реактивных элементов  и определяется как разность длин векторов:
и определяется как разность длин векторов:
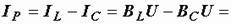
 (см. рис. 1, б и 2, а).
(см. рис. 1, б и 2, а).

Рис. 2 Треугольники токов и проводимостей
Разделив все стороны треугольника токов на  , получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями:
, получим треугольник проводимостей (рис. 2.32, б), стороны которого связаны следующими соотношениями:
 ,
,  ,
, 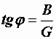 ,
,  .
.
Пояснения к работе:
Студент при выполнении работы должен хорошо представлять, какие особенности реализуются в электрической цепи.