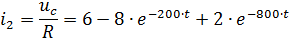САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПЕТРА ВЕЛИКОГО
ИНСТИТУТ ЭНЕРГЕТИКИ И ТРАНСПОРТНЫХ СИСТЕМ
Кафедра «Теоретическая электротехника и электромеханика»
КУРСОВая РАБОТА
по дисциплине «Теоретические основы электротехники»
Анализ процессов в электрических цепях
Выполнил
студент гр. 23231/4 __________________ Н.В. Варнаков
Руководитель
доцент, к.т.н. __________________ С.Е. Виноградов
«___»_______________ 2018__ г.
Санкт-Петербург
Расчет установившихся синусоидальных режимов
В сложной электрической цепи при заданных параметрах источников и потребителей, рассчитать токи и напряжения в установившемся режиме в каждой ветви с помощью методов контурных токов и узловых напряжений.
Определить мощности, потребляемые в ветвях, проверить баланс активной и реактивной мощности в цепи.
Записать мгновенные значения токов во всех ветвях.
Построить на комплексной плоскости векторную диаграмму тока и напряжений в одной из ветвей, содержащей не менее двух элементов.
Расчет переходного процесса в цепи второго порядка
В заданной электрической цепи рассчитать токи и напряжения классическим методом и построить графики их изменения после коммутации.
Определить один из токов операторным методом.
 |
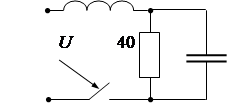U = 240 В, L = 0,25 Гн, С = 25 мкФ, сопротивления резисторов указаны на схеме в омах.
Расчет переходных процессов в однородных линиях
Две однородные воздушные линии без потерь включаются со стороны зажимов 1-1 под действие постоянного напряжения U 0 =360 кВ. Волновые сопротивления линий одинаковы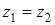 
= 400 Ом. Длина первой линии 200 км, а второй – 100 км.
На стыке двух линий включен четырехполюсник, а в конце второй линии нагрузка.
На стыке двух линий:
 |
В конце 2-й линии:
 |
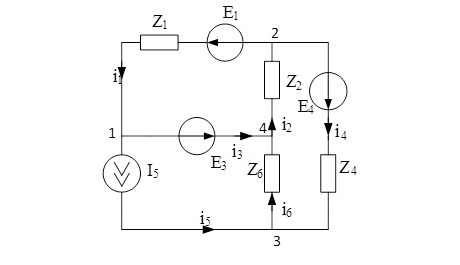
Расчет установившихся синусоидальных режимов
Расчётная схема для анализа синусоидальных режимов
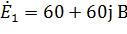
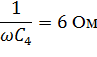
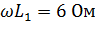
Расчёт цепи синусоидального тока методом контурных токов.
Заменим исходную цепь на цепь для расчёта.
Где
=60+60j B;
=360 B;
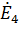=120-180j B;
=4+6j A;
=6j Ом;
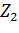=6+2j Ом;
=6-2j Ом;
=6-4j Ом;
В контуре 3 содержится идеальный источник тока. В нем я принимаю значение контурного тока равным току источника, а для остальных контуров составляю уравнения в матричной форме.
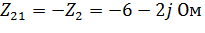
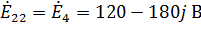
Далее решаю систему уравнений и получаю матрицу значений контурных токов.
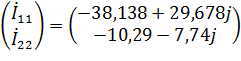
Тогда
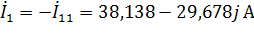
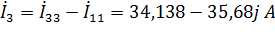
Расчёт цепи синусоидального тока методом узловых напряжений.
На одном из зажимов идеального источника ЭДС выбираю точку 0, тогда напряжение на зажимах 10 равно: 
= 
Запишу систему уравнений в матричном виде.
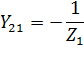
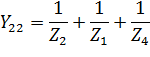
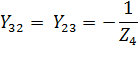
Решаю систему уравнений и получаю.
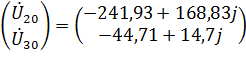
Найду значение токов
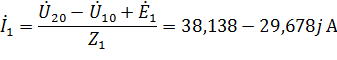
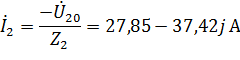
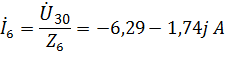
Токи в ветвях с идеальными источниками
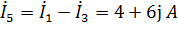
Построение векторной диаграммы.
Расчёт цепи при переходных процессах.
Задание: В заданной цепи для указанных параметров рассчитать в переходном процессе все токи и напряжение на конденсаторе, построить графики найденных токов и напряжения. Найти один из токов операторным методом.
U = 240 В, L = 0,25 Гн, С = 25 мкФ, R1=40
Классический метод расчёта переходных процессов.
Начальные условия:
Система уравнений по законам Кирхгофа:
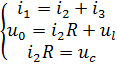
Решаю данную систему уравнений и привожу её к дифференциальному уравнению второго порядка.
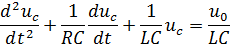
Решаю дифференциальное уравнение в виде
где 
- значение в установившемся режиме, 
- преходящая
Нахожу корни характеристического уравнения
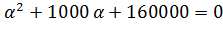
Корни этого выражения равны
После коммутации
Установившаяся составляющая уравнения равна, т.е. напряжение на конденсаторе равно 240 В.
Уравнение запишется в виде
Подставляю в уравнение t=0
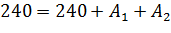
Нахожу ток, как производную напряжения по времени, делённую на ёмкость конденсатора
Нахожу начальный ток в ветви с конденсатором
Запишу полученные уравнения в систему.
Решая систему уравнений получаю, что 
Напряжение на конденсаторе:
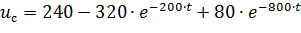
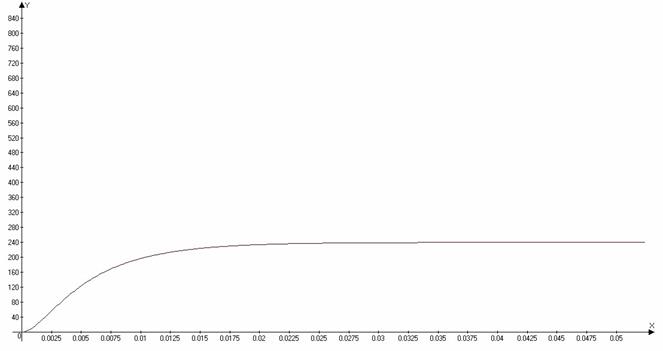
Нахожу токи:
