Итак, четко выделим АЛГОРИТМ НАХОЖДЕНИЯ ТОКОВ

1. По закону Ома находим общий ток 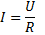или определяем силу тока по формуле: І = √ P/ R

2. Находим в цепи участок (один или несколько резисторов), в котором проходит общий ток. Для этого участка сила тока в резисторе равна общему току, например, I_общ = I₁.

3. Определяем напряжение на разветвлении по формуле:

^{, где RАВ --сопротивление разветвления}

4. Определить силу тока в ветвях

4.1 Находим силу тока в первой ветви (сопротивление R_123,)

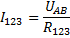
Определяем ток каждого резистора ветви, так как R_1,R₂ и R₃ включены последовательно:

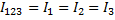
4.2.Определяем ток во второй ветви (сопротивление R_45,)

4.2.1.Определяем ток каждого резистора ветви (т.к. R₄ и R₅ включены последовательно)

Методические указания к решению задач по теме «Однофазные электри-ческие цепи переменного синусоидального тока». В этих цепях, так же как и в цепях постоянного тока, при решении задач используют закон Ома, первый закон Кирхгофа, формулы мощности, свойства последовательного и параллельного соединений. Однако из-за того, что в переменном токе действует три вида совершенно различных по характеру сопротивлений (активное R, индуктивное X_L и ёмкостное X_C) форма записи законов изменяется. Иначе устанавливается связь и между однородными электрическими величинами. Так, при последовательном соединении в постоянном токе общее сопротивление было равно арифметической сумме сопротивлений, в переменном токе берется уже геометрическая сумма R, X_L и X_C. Геометрически складывается также напряжения и мощности на этих сопротивлениях.

В разветвлённых цепях постоянного тока первый закон Кирхгофа устанавливая связь между токами в арифметической форме, в переменном токе эта связь будет геометрическая. В связи с особенностями однофазных электрических цепей синусоидального тока рассмотрим основные соотношения между электрическими величинами для наиболее характерных цепей.

Однофазная электрическая цепь переменного синусоидального тока с последовательным соединением активного R, индуктивное X_L и ёмкостное X_C сопротивлений (рис.11)

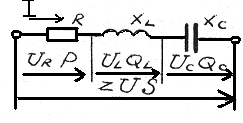
Рис.11

На этой схеме:

I, А – ток, потребляемый цепью, единица измерения – ампер;

R, Ом – активное сопротивление цепи, единица измерения – Ом;

U_R, В – напряжение на активном сопротивлении, единица измерения – вольт;

P, Вт – активная мощность цепи, единица измерения – ватт;

X_L, Ом – индуктивное (реактивное) сопротивление цепи, единица измерения – Ом;

U_L, В – напряжение на индуктивном сопротивлении, единица измерения – вольт;

Q_L, ВАр – индуктивная (реактивная) мощность, единица измерения Q_L, вар – индуктивная (реактивная) мощность, единица измерения вольт-ампер реактивный;

X_C, Ом – ёмкостное (реактивное) сопротивление цепи, единица измерения – Ом;

U_C, В – напряжение на ёмкостном сопротивлении, единица измерения – вольт;

Q_C, ВАр – ёмкостная (реактивная) мощность, единица измерения – вольт-ампер реактивный;

Z, Ом – полное сопротивление цепи, единица измерения – Ом;

U, В – полнле напряжение, подведенное к зажимам цепи, единица измерения – вольт;

S, ВА – полная мощность, единица измерения – вольт-ампер.

На основании закона Ома напряжение на активном, индуктивном и ёмкостном сопротивлениях могут быть определены по формулам:

U_R=I*R U_L=I*X_L U_C=I*X_C

При этом следует иметь в виду, что U_R – совпадаетпо фазе с током, – U_L – опережает по фазе ток на 90⁰, U_C – отстаёт от тока на 90⁰.

Результирующее напряжение U представляет геометрическую сумму напряжений U_R, U_L и U_C. На рис. 12 представлена векторная диаграмма этих направлений.

Рис. 12

 

Результирующее напряжение U,которое является напряжением, подведённым к зажимам цепи, можно найти не только графически (в этом случае диаграмма должна быть построена в масштабе), но и математически, на основании теоремы Пифагора:

U =√U²_R +(U_L -U_C)²

Если каждое из напряжений на векторной диаграмме (рис.12) разделить на ток 1, то получится фигура, подобная векторной диаграмме, которая будет называться треугольником сопротивлений (рис.13) т.к.

Рис. 13

 

R =U_R /I, X _L=U_L /I, X_C =U_C /I, Z=U/I.

Из треугольника сопротивлений следует, то Z=√R²+(X_L-X_C)²

 

Если каждое из напряжений на векторной диаграмме (рис.12) умножить на ток I, то получится фигура, подобная векторной диаграмме, которая будет называться треугольником мощностей (рис.14), так как

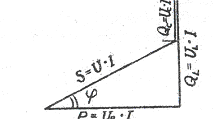Рис. 14

 

P=U_R*I Q_L=U_L*I Q_C=U_C*I S=U*I

Из треугольника мощностей следует, что S=√P²+(Q_L-Q_C)²

Используя закон Ома для каждого элемента цепи, мощность можно также найти по формулам:

P=I²*R, Q_L=I²*X_L, Q_C=I²*X_C, S=I²*Z или

P=I²_R/R, Q_L=I²_L*X_L, Q_C=I²_C*X_C, S=I²*Z

Из треугольника мощностей (рис.14) также следует, что

P=S*cos ϕ P=U*I*cos ϕ

Q=S*sin ϕ Q=U*I*sin ϕ

где Q=Q_L-Q_C - результирующая реактивная мощность.

Анализируя векторную диаграмму напряжений (рис.12), треугольник сопротивлений (рис.13), треугольник мощностей (рис.14), можно сделать вывод, что при U_L>U_C (X_L>X_C) результирующий вектор напряжения U опережает вектор тока 1 на угол ϕ <90⁰, а при U_L<U_C (X_L<X_C) результирующий вектор напряжения отстает от вектора тока на угол ϕ.

Тригонометрические функции угла сдвига фаз можно записать в виде: cos ϕ=U_R/U cos ϕ=R/Z cos ϕ=P/S

sin ϕ= (U_L-U_C)/U sin ϕ=(X_L-X_C) /Z sin ϕ=Q_L-Q_C/S

cos ϕ = P/S – называется коэффициентом мощности

 

Особенности расчета цепи при другой комбинации элементов схемы.

При отсутствии одного из реактивных сопротивлений все электрические параметры определяются по вышеперечисленным формулам. При этом из них нужно исключить параметры с индексом отсутствующего элемента.

 

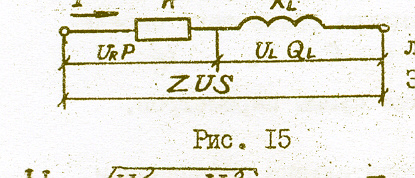
Рис. 15

 

На рис.15 изображена цепь с последовательным соединением R и X_{L .} Значит X_С отсутствует, поэтому:

U=√U²_R+U²_L Z=√R²+X²_L S=√P²+Q²_L Q=Q_L

sin ϕ = U_L/U sin ϕ = X_L /Z sin ϕ = Q_L/S

Векторная диаграмма, треугольник сопротивлений и треугольник мощностей будет иметь вид, изображенный на рис.16

Векторная диаграмма, треугольник сопротивлений и треугольник мощностей будет иметь вид, изображенный на рис.16

 

Рис.16

 

 

 

Рис.17

 

На рис.17 изображенная цепь с последовательным соединением R и X_С, элемент X_L отсутствует, поэтому:

U=√U²_R+U²_С Z=√R²+X²_С S=√P²+Q²_С Q=Q_L sin ϕ = - U_С/U sin ϕ = - X_С /Z sin ϕ = - Q_С/S

Векторная диаграмма, треугольник сопротивлений и треугольник мощностей будет иметь вид, изображенный на рис.18

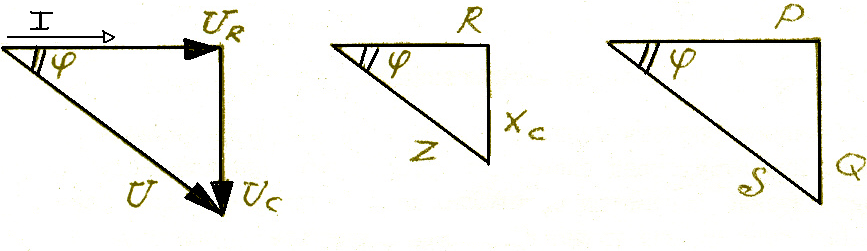
Рис.18

 

Если схема имеет несколько одинаковых по характеру элементов, то в этом случае электрические параметры опять-таки определяются по формулам, приведенным для цепи с R, X_С, X_L, при этом в них нужно ввести арифметические суммы параметров, имеющих одинаковые индексы.

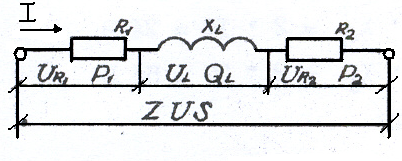
На рис.19 изображена цепь с последовательным соединением R₁, X_L и R ₂ (т.е. в схеме два активных

рис.19 сопротивления), поэтому:

U = √ (U_R1+U_R2)²+U²_L Z = √(R₁+R₂)²+X²_L S =√(P₁+P₂)²+Q²_L

cos ϕ = (U_R1+U_R2)/U cos ϕ = (R₁+R₂) /Z cos ϕ = (P₁+P₂)/S

Векторная диаграмма, треугольник сопротивлений и треугольник мощностей будет иметь вид, изображенный на рис.20 Рис.20

 

Пример 2.

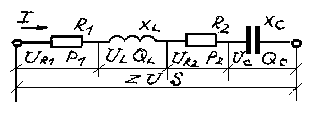Дано: U=50 В R₁=9 Ом X_L=12 Ом X_С=27 Ом R₂=11 Ом

Определить: Z, I, U_R1, U_L, U_C, P, Q, S, cos ϕ.

Построить в масштабе векторную диаграмму напряжений.

 

Решение

1. Определяем полное сопротивление цепи

Z = √ (R₁+R₂)²+(X_L - X_C)² = √(9+11)²+(12 - 27)² =25 Ом

2. Определяем ток цепи

I=U/Z =50/25=2A

3. Определяем падение напряжения:

- на активном сопротивлении R₁ U_R1=I*R₁ =2*9=18 B

- на активном сопротивлении R₂ U_R2=I*R₂ =2*11=22 B

- на индуктивном сопротивлении U_L=I*X_L =2*12=24 B

- на ёмкостном сопротивлении U_C=I*X_C =2*27=54 B

4. Определяем коэффициент мощности цепи

cos ϕ = (R₁+R₂) /Z =9+11/25=0,8.

5. Угол сдига фаз ϕ находим по синусу во избежание потери знака угла (косинус является четной функцией)

sin ϕ = (X_L-X_C)/ Z = ( 12-27)/25 = - 0,6

Используя микрокалькулятор или таблицы Брадиса, находим ϕ = - 36⁰ 52'

6. Определяем активную мощность цепи

P=U*I*cosϕ = 50*2*0,8=80 Вт

Активную мощность можно найти по формулам

P=P₁+P₂ = I² *R₁ + I² *R₂

P=P₁+P₂ = U_R1*I + U_R2*I

P=P₁+P₂ = U² _R1 /R₁ + U²_R2 /R₂

Проверьте это.

7. Определяем реактивную мощность

Q=U*I*sin ϕ = 50*2*(-0,6) = - 60 ВАр.

Реактивную мощность можно также найти по формулам

Q=Q_L-Q_C= I² *X_L - I² *X_C

Q=Q_L+Q_C= U_L *I - U_C *I

Q=Q_L+Q_C= U² _L /X_L - U²_C /X_C

Проверьте это.

7. Определяем полную мощность цепи

S=U*I =50*2=100 BA

Полную мощность можно также найти по формулам

S=I²*Z S=U²/Z

S=√P²+Q² Q=Q_L- Q_C

Проверьте это.

Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току и по напряжению

m_i = 1 A/ см m_u= 5 B/ см

Здесь m_i и m_u – масштабные коэффициенты. Они показывают, сколько ампер или вольт содержится в 1 см. Масштаб можно задавать и графически, см. рис.22

Порядок построения.

От точки 0 горизонтально вправо проводим вектор тока общий для всей цепи. В выбранном масштабе его длина будет

l₁=I/m₁ =2 А/1 А/см=2 см.

Рис.22

 

7. Вектор активного напряжения U_R1 совпадает по фазе с током, угол сдвига фаз между ними равен 0, поэтому откладываем его вдоль вектора тока от точки 0 вправо.

Его длина

l_UR1 = U_R1/m_U = 18 В/5 В/см = 3,6 см

8. От конца вектора U_R1 откладываем вправо вдоль вектора тока вектор активного напряжения U_R2.

Его длина

l _{UR 2} = U_R2/m_U = 22 В/5 В/см = 4,4 см

9. От конца вектора U_R2 откладываем вертикально вверх вектор падения напряжения U_L на индуктивном сопротивлении, так как он опережает ток на угол 90⁰.

Его длина

l u_L = U_L/m_U = 24 В/5 В/см =4,8 см

10. От конца вектора U_L откладываем вертикально вниз вектор падения напряжения U_С на ёмкостном сопротивлении, т.к. он опережает ток на угол 90⁰.

Его длина

l _UC = U_C/m_U = 54 В/5 В/см = 10,8 см

Геометрическая сумма векторов U_{R1 ,} U_R2, U_L и U_C должна быть равна полному напряжению U, приложенному к зажимам цепи, т.е.

U = U_R1 +U_R2+U_L+U_C

Измерив длину этого вектора, убеждаемся, что она L_U =10см. Это значит, что с учетом масштаба его величина будет:

U = l_U*m_U = 10см*5 В/см = 50 В

По условию задачи именно такое напряжение приложено к зажимм цепи.

Примечание:

Если в выбранном масштабе вектор суммарного напряжения не будет равен приложенному к зажимам цепи напряжению, то это будет говорить об ошибке, допущенной в решении задачи или в построении векторной диаграммы. Её нужно найти и устранить.

Чаще всего наблюдаются ошибки, связанные с искажением масштабов при построении векторной диаграммы пользуйтесь чертёжным инструментом. Выполняйте диаграмму точно и аккуратно.

 

Методические указания к решению задач по трёхфазным электрическим цепям переменного синусоидального тока.

 

В трёхфазных цепях потребители соединяют по схеме «звезда» или «треугольник».

При соединении приемников энергии звездой линейные напряжения обозначаются U_АВ, U_ВС, U_СА, а в общем виде -U_С; фазные напряжения обозначаются U_А, U_В, U_С, а в общем виде - U_ф.

Токи обозначаются - I_А, I_В, I_С, причем ток линейный равен току фазному, поэтому в общем виде I_А=I_ф.

При наличии нулевого провода при любой нагрузке, а при равномерной нагрузке и без нулевого провода U_A=√3*U_ф (линейное напряжение больше фазного в √3 раз).

При равномерной нагрузке фаз активная мощность всей цепи.

Р=√3U_A*I_A*cosγ_ф или P=3U_ф*I_ф*cosγ_ф

При неравномерной нагрузке мощность всей цепи

Р=Р_ф1+Ф_ф2+Р_ф3 или P=U_ф*I_ф*cosγ_ф

При соединении потребителей треугольником фазное напряжение равно линейному: U_ф=U_А, обозначаются напряжения U_АВ, U_ВС, U_СА.

Фазные токи обозначаются I_АВ, I_ВС, I_СА, в общем виде I_ф.

Линейные токи обозначаются I_А, I_В, I_С, в общем виде I_А.

При равномерной нагрузке фаз I_А=√3*I_ф

При неравномерной нагрузке линейные токи определяются на основании первого закона Кирхгофа из векторной диаграммы, как геометрическая разность фазных токов.

При соединении приемников энергии звездой сеть может быть четырехпроводной – при наличии нулевого провода, или трехпроводной – без нулевого провода.

При соединении приемников энергии треугольником сеть может быть только трехпроводной.

 

Пример 4.

В четырехпроводную сеть (рис.27) трехфазного тока с линейным напряжением U_Л =380 В включены по схеме «звезда» три группы электрических ламп накаливания одинаковой мощности. В каждой группе лампы соединены паралельно. В среднем сопротивление одной лампы составляет R_ламп= 484 Ом.

Дано:

U_Л =380 В

R _ламп=484 Ом

n _А=88 шт.

n _В=33 шт

n _С=55 шт.

Определить: U _ламп , I_ламп , Р _ламп, I_А, I_В, I_С, Р_А, Р_В, Р_С, Р.

I₀ – графически из векторной диаграммы Рис.27

 

Первая группа ламп включена в фазу А, число ламп в ней n_А=88 шт.

Вторая группа ламп включена в фазу В, число ламп в ней n_В=33 шт.

Третья группа ламп включена в фазу С, число ламп в ней n_С=55 шт.

Определить ток I ламп, напряжение U ламп, мощность Р_ламп , на которую рассчитана лампа; токи I_А, I_В, I_С, протекающие в фазах и линейных проводах; мощности Р_А, Р_В, Р_С, Р, потребляемые фазами и всей цепью. Построить в масштабе векторную диаграмму напряжений и токов и из неё графически определить величину тока в нулевом проводе I₀. Построить в масштабе векторную диаграмму напряжений и токов.

1. U _Л – запись линейных напряжений U_АВ, U_ВС, U_СА, в общем виде

По условию задачи U_АВ =U_ВС = U_СА = 380 В.

Тогда фазные напряжения U_А, U_В, U_С в общем виде U_Ф будут: U_Ф= U_Л/√3 = 380/√3 = 220 В, таким образом, U_А =U_В = U_С=220 В.

2. Все лампы цепи включены на фазные напряжения, поэтому U _ламп =U_Ф=220 В.

3. Ток ламп по закону Ома

I _ламп =U _ламп /R _ламп,=220/484=0,455 А

4. Мощность лампы

Р_ламп =U _ламп * I _ламп,=220*0,455=100 Вт

Мощность лампы модно также найти по формулам

Р _ламп =U² _ламп /R _ламп или Р _ламп =I² _ламп *R _ламп

Проверьте это.

5. Сопротивления фаз (они активные)

R _А = R _ламп /П _А=484/88=5,5 Ом

R _В = R _ламп /П _В=484/33=14,6 Ом

R _С = R _ламп /П _С=484/55=8,8 Ом

6. Токи фаз по закону Ома

I _А=U _А/R _А=220/5,5=40 А

I _В=U _В/R _В=220/14,6=15 А

I _С=U _С/R _С=220/8,8=25 А

Фазные токи ламп можно было найти по значению тока лампы и количеству ламп в фазе I_A=I_ламп*П_А, I_В=I_ламп*П_В, I_С=I_ламп*П_С.

Проверьте это.

7. Мощности, потребляемые фазами (они активные)

Р _А=U _А* I_А=220*40=8800 Вт

Р _В=U _В* I_В=220*15=3300 Вт

Р _С=U _С* I_С=220*25=5500 Вт

Другие способы определения мощностей фаз:

Р _А=U ²_А /R _А Р _В=U ²_В /R _В Р _С=U ²_С /R _С

Р _А= I²_А /R _А Р _В= I²_В /R _В Р _С= I²_С /R _С

Р _А= Р_ламп *n _А Р _В= Р_ламп *n _В Р _С= Р_ламп *n _С

8. Мощность, потребляемая цепью,

Р=Р_А+Р_В+Р_С=8800+3300+5500=17600 Вт.

9. Векторная диаграмма напряжений и токов. Построение векторной диаграммы начинаем с вывода масштаба для напряжения и тока (в контрольной работе эти масштабы вам заданы).

Пусть m_U =44 В/см, m_I=10 А/см.

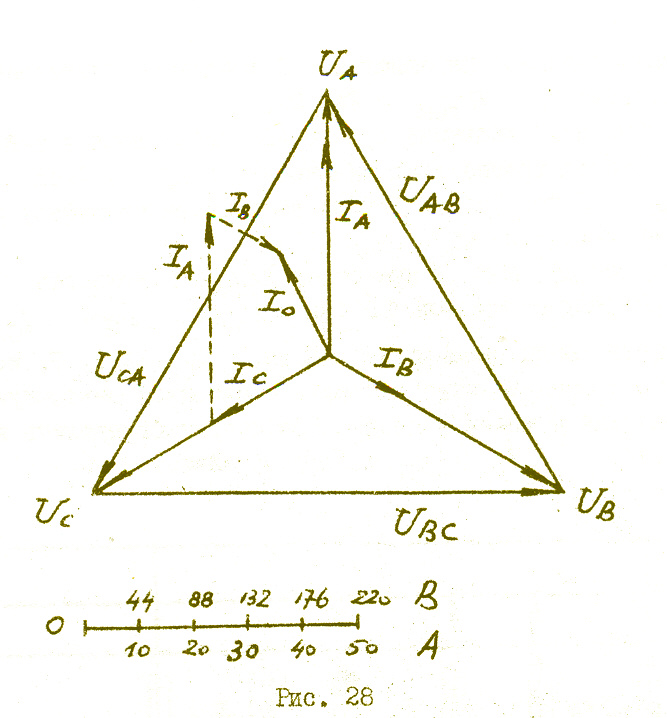
Порядок выполнения, рис.28.

1. Из точки 0 проводим три вектора фазных напряжений U_А, U_В и U_С, углы между которыми составляют 120 ⁰ (эти углы строят с максимально возмодной точностью, используя циркуль или транспортир). В выбранном масштабе их длина будет l _UФ=U_Ф/m_U=220 В/44 В/см=5 см.

4. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений U_АВ, U_ВС, U_СА.

Направление этих векторов совпадает с обходом против часовой стрелки. Возможны и другие способы изображения линейных напряжений (см. их в учебной литературе).

Измерив векторы линейных напряжений, можно убедиться, что с учетом масштаба их длина будет равна 380 В.

 

5. Нагрузка фаз активная (электрические лампы накаливания обладают активным сопротивлением), поэтому токи I_А, I_В, I_С будут совпадать по фазе с соответствующими фазными напряжениями. В выбранном масштабе их длина будет:

l _IA= I_A/m_I = 40 А/10 А/см = 4 см

l _IB= I_B/m_I = 15 А/10 А/см = 1,5 см

l _IC= I_C/m_I = 25 А/10 А/см = 2,5 см

4. Геометрически складываем токи I_А, I_В, I_С и получаем ток в нулевом проводе:

I₀ = I_А + I_В + I_С

При этом векторы токов можно складывать в любой последовательности. Так, на диаграмме к концу вектора I_С путем паралельного переноса пристроен вектор I_А, к концу вектора I_А пристроен путем паралельного переноса вектор I_В. Точка 0 соединена с концом вектора I_В – это и есть ток в нулевом проводе I₀ . Величина тока в нулевом проводе

I₀= l _Io*m_I = 2,2 см*10 А/см = 22 А

Т.е. ток в нулевом проводе определен графически, его величина

I₀=22 А

Пример 5.

В трехпроводную сеть (рис.29) трехфазного тока с линейным напряжением U_A =220 В включены по схеме «треугольник» три группы электрических ламп накаливания одинаковой мощности. В каждой группе

лампы соединены паралельно. В среднем сопротивление одной лампы составляет R _ламп = 242 Ом.

Первая группа ламп включена в фазу АВ, число ламп в ней n _АВ =11 шт.

Вторая группа ламп включена в фазу ВС, число ламп в ней n _ВС =22 шт. Третья группа ламп включена в фазу СА, число ламп в ней n _СА =33 шт.

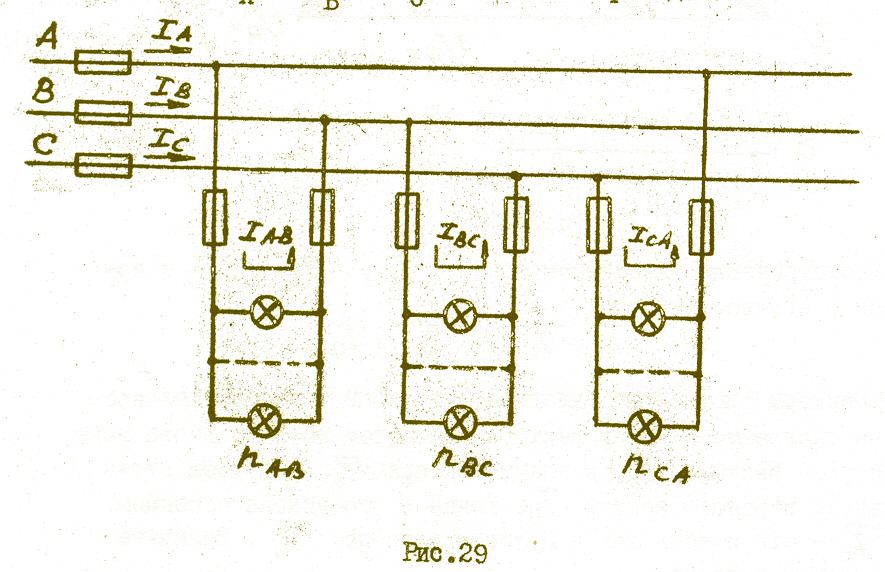Определить ток I ламп, напряжение U _ламп и мощность Р _ламп , на которые расчитана лампа; токи I_АВ, I_ВС, I_СА , протекающие в фазах цепи; мощности Р_АВ, Р_ВС, Р_СА, Р, потребляемые фазами и всей цепью. Построить в масштабе векторную диаграмму напряжений и токов и из неё графически определить величину токов I_А, I_В, I_С в линейных проводах.

 

 

Рис.29

 

Дано:

U _A=220 В R _ламп=242 Ом n _АВ=11 шт. n _ВС=22 шт n _СВ=33 шт.

Определить: U _ламп , I_ламп , Р _ламп, I_АВ, I_ВС, I_СА, Р_АВ, Р_ВС, Р_СА, Р.

I_А, I_В, I_С, – графически из векторной диаграммы.

Построить в масштабе векторную диаграмму напряжений и токов.

1. U _А запись линейных напряжений U_АВ, U_ВС, U_СА. в общем виде. По условию задачи U_АВ=U_ВС = U_СА=220 В. При соединении «треугольником» линейное напряжение равно фазному, поэтому U_A=U_Ф.

6. Все лампы цепи включены на фазное напряжение, поэтому U_ламп= U_Ф = = 220 В.

7. Ток лампы по закону Ома

I _ламп= U _ламп/R _ламп=220/242=0,909 А

8. Мощность лампы

Р_ламп= U _ламп*I _ламп=220*0,909=200 Вт

Мощность лампы можно также найти по формулам

Р_ламп= U² _ламп/R _ламп или Р_ламп= I² _ламп*R _ламп

Проверьте это.

9. Сопротивления фаз (они активные)

R _АВ = R _ламп /n _АВ=242/11=22 Ом

R _ВС = R _ламп /n _ВС=242/22=11 Ом

R _СА = R _ламп /n _СА=242/33=7,33 Ом

10. Токи фаз по закону Ома

I _АВ=U _АВ/R _АВ=220/22=10 А

I _ВС=U _ВС/R _ВС=220/11=20 А

I _СА=U _СА/R _СА=220/7,33=30 А

11. Фазные токи можно было найти по значению тока лампы и количеству ламп в фазе I_AВ=I_ламп*П_АВ, I_ВС=I_ламп*П_ВС, I_СА=I_ламп*П_СА

Проверьте это.

12. Мощности, потребляемые фазами (они активные)

Р _АВ=U _АВ* I_АВ=220*10=2200 Вт

Р _ВС=U _ВС* I_ВС=220*20=4400 Вт

Р _СА=U _СА* I_СА=220*30=6600 Вт

Другие способы определения мощностей фаз:

Р _АВ=U ²_АВ /R _АВ Р _ВС=U ²_ВС /R _ВС Р _СА=U ²_СА /R _СА

Р _АВ= I²_АВ /R _АВ Р _ВС= I²_ВС /R _ВС Р _СА= I²_СА /R _СА

Р _АВ= Р_ламп *n _АВ Р _ВС= Р_ламп *n _ВС Р _СА= Р_ламп *n _СА

Проверьте это.

13. Мощности, потребляемая трехфазной цепью

Р=Р_АВ+Р_ВС+Р_СА=2200+4400+6600=13200 Вт.

14. Векторная диаграмма напряжений и токов (рис.30). Построение векторной диаграммы начинают с выбора масштаба для напряжения и токов (в контрольной работе эти масштабы вам заданы).

Пусть m_U =55 В/см, m_I=10 А/см.

Порядок выполнения.

Из точки 0 проводим три вектора фазных напряжений U_АВ, U_ВС и U_СА, углы между которыми составляют 120 ⁰ (эти углы строят с максимально возможной точностью, используя циркуль или транспортир). В выбранном масштабе их длина будет l_UФ = U_Ф/m_U = 220 В/55 В/см = 4 см.

Следует иметь в виду, что эти векторы напряжений одновременно являются и векторами линейных напряжений.

 

Рис. 30

 

 

Нагрузка фаз активная (электрические лампы наккаливания обладают активным сопротивлением), поэтому токи I_АВ, I_ВС, I_СА будут совпадать по фазе с соответствующими фазными напряжениями. В выбранном масштабе их длина будет:

l_IAВ =I_AВ/m_I=10 А/10 А/см=1 см

l_IBС =I_BС/m_I=20 А/10 А/см=2 см

l_ICА =I_CА/m_I=30 А/10 А/см=3 см

Соединив концы векторов фазных токов, получим треугольник линейных токов I_А, I_В, I_С, направление этих векторов совпадает с обходом по часовой стрелке. Возможны и другие способы изображения линейных токов (см. их в учебной литературе).

Измерив длину линейных токов и учитывая масштаб, определяем их значение

l_A=m_I /I_IA=10 А/см*3,6см=36 А

l_В=m_I /I_IВ=10 А/см*2,6см=26 А

l_С=m_I /I_IС=10 А/см*4,4см=44 А