ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ
Методические указания к решению задач по теме «Электрические цепи постоянного тока». Решение их требует знания закона Ома, формул мощности, первого закона Кирхгофа, свойств последовательного и параллельного соединения резисторов.
Краткие сведения о перечисленных выше понятиях.
Закон Ома для участка цепи

Рис. 1
На рис.1 изображен резистор, представляющий участок электрической цепи, где: U – электрическое напряжение на резисторе (участке цепи); R – электрическое сопротивление резистора (участка цепи); I – сила тока на резисторе (участке цепи).
Между этими электрическими величинами существует строго определенная связь. Она устанавливается законом Ома:
Сила тока 1 на участке электрической цепи прямо пропорциональна напряжению U на его зажимах и обратно пропорциональна сопротивлению R этого участка цепи, т.е.
I=U/R, тогда U=I*R, а R=U/I
Единицы измерения:
тока I – А (ампер), напряжения U – В (вольт),
сопротивления R – Ом (ом).
Примечание:
Единицы измерения всех электрических величин, получивших название в честь ученых, пишутся с прописной (заглавной) буквы, поэтому А, В, Ом.
Мощность, потребляемая цепью Мощность – это скорость, с которой происходит преобразование энергии. Для участка цепи, изображенного на рис. 1, электрическая мощность может быть определена по формулам:
P=U*I, P=I2*R, P=U2/R
Единица измерения мощности Р – Вт (ватт).
 Первый закон Кирхгофа
Первый закон Кирхгофа
На рис. 2 показана часть электри-ческой схемы с электрическим узлом или точкой разветвления (см. точку А). Это такая точка электрической схемы, где соединены три или большее число проводов (на рис. 2 таких проводов 5). Рис. 2
Первый закон Кирхгофа устанавливает сотношение междутоками в узле. Он формулируется так:
Сумма токов, направленных к узлу, равна сумме токов, направленных от него. Для узла А можно написать:
I1+I2 = I3+I4+I5
или так: I1+I2+(-I3)+(-I4)+(-I5) = 0
а в общем виде ∑I=0, т.е. алгебраическая сумма токов в узле равна нулю. При этом токи, направленные от узла, считаются отрицательными.
Последовательное соединение резисторов (рис. 3)
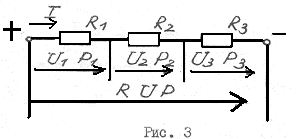
Рис. 3
Свойства последовательного соединения:
1. На всех резисторах (участках) этой цепи протекает один и тот же ток: I1= I2= I3= I
2. Эквивалентное сопротивление последовательной цепи равно сумме сопротивлений её резисторов (участков): R = R1+R2+R3
3. Напряжение на зажимах цепи равно сумме падений напряжений на её отдельных резисторах (участках): U = U1+U2+U3
4. Мощность, потребляемая цепью, равна сумме мощностей, потребляемых каждым из резисторов (участков): Р = Р1+Р2+Р3
При решении задач, содержащих последовательное соединение элементов, следует учитывать не только вышеперечисленные свойства, но и правильно применять закон Ома и формулы мощности, необходимость использования которых может возникнуть как на отдельном участке, так и для всей цепи в целом. Для схемы, изображенной на рис.3, они должны быть записаны в виде:
I=U1/R1 I=U2/R2 I=U3/R3 I=U/R
P1=U1*I1 P2=U2*I2 P3=U3*I3 P=U*I P1=I12*R1 P2=I22*R2 P3=I32*R3 P=I2*R P1=U12/R1 P2=U22/R2 P3=U32/R3 P=U2/R
Паралельное соединение резисторов (рис. 4)

Рис.4
Свойства параллельного соединения:
1. На всех резисторах (участках) такой цепи действует одно и то же напряжение: U1=U2=U3=U
2. Ток в неразветвлённой части цепи равен сумме токов её ветвей: I=I1+I2+I3 (это следует из 1 закона Кирхгофа).
3. Полная (эквивалентная) проводимость параллельной цепи равна сумме проводимостей её резисторов (участков): G=G1+G2+G3 или 1/R=1/R1+1/R2+1/R3
4. Мощность, потребляемая цепью, равна сумме мощностей, потребляемых каждым из резисторов (участков): Р = Р1+Р2+Р3
Примечание:
При определении эквивалентного сопротивления трёх и большего числа резисторов рекомендуется вначале найти проводимость цепи, а затем её сопротивление.
G = 1/R1 + 1/R2 +…+ 1/Rп; R = 1/G, Ом
При определении эквивалентного сопротивления двух резисторов рекомендуется применить формулу: R = R1*R2/(R1+R2), Ом
При решении задач, содержащих параллельное соединение элементов, следует учитывать не только вышеперечисленные свойства, но и правильно применять закон Ома и формулы мощности, необходимость использования которых может возникнуть как на отдельном участке, так и для всей цепи в целом. Для схемы, изображённой на рис. 4 они должны быть записаны в виде:
I=U/R1 I=U/R2 I=U/R3 I=U/R
P1=U*I1 P2=U*I2 P3=U*I3 P=U*I P1=I12*R1 P2=I22*R2 P3=I32*R3 P=I2*R P1=U2/R1 P2=U2/R2 P3=U2/R3 P=U2/R
Обратитесь к подобным формулам последовательного содержания. Проанализируйте их. Разберитесь, что в них общего и чем они отличаются друг от друга.
Пример 1:

Рис. 5
Для схемы, приведённой на рис. 5 и представляющей смешанное соединение сопротивлений, известно, что U=250В, R1=14 Ом, R2=20 Ом, R 3=50 Ом, R 4=200 Ом, R 5=40 Ом, R 6=150 Ом, R 7=60 Ом. Определить эквивалентное сопротивление R этой цепи, ток I и мощность P, потребляемые цепью, а также токи I1, I2, I3, I4, I5, I6, I7, напряжения U1, U2, U3, U4, U5, U6, U7 и мощности P1, P2, P3, P4, P5, P6, P7 на каждом резисторе. Проверить решение задачи методом баланса мощностей.
Перед решением примера 1 необходимо внимательно прочитать общие методические указания к решению задач 1….5 и только после этого приступить к решению.
В этом примере и в задачах индекс тока, протекающего через резистор, индекс напряжения на нём и индекс мощности, потребляемой резистором, соответствуют индексу резистора. Например, на рис. 5 резистор R3 характеризуется током I3, напряжением U3, мощностью P3 и т.д.
Схема электрической цепи, изображенная на рис. 5, представляет собой смешанное резисторов (оно состоит из последовательных и паралельных соединений элементов схемы), эквивалентное сопротивление такой цепи находится путем постепенного упрощения схемы и «свертывания» её так, чтобы получить одно сопротивление. При расчете токов в отдельных ветвях схему «развертывают» в обратном порядке.
Решение
Два резистора R3 и R4 соединены параллельно, поэтому их эквивалентное сопротивление R34 = R3 R4 / (R3 +R4) = 50*200 / (50+200)=40 Ом
теперь схема принимает вид, показанный на рис. 6 на этой схеме выделены буквами три участка (ав, вс, сд), которые соединены друг с другом последовательно.

Рис. 6
5. Резисторы R 2 и R 34 (см. рис. 6) соединены последовательно, их общее сопротивление: R 234 = R 2 +R 34 =20+40=60 Ом.
Соответствующая схема приведена на рис. 7
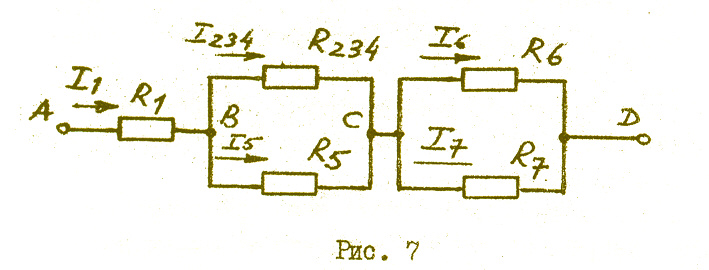
Рис. 7
3. Резисторы R 234 и R 5 соединены параллельно, их общее сопротивление RВС= R234* R5 / (R234 +R5) = 60*40 / (60+40)=24 Ом
Теперь схема цепи примет вид, приведенный на рис. 8

Рис.8
4. Резисторы R 6 и R 7 соединены паралельно, их общее сопротивление
RСД=R6* R7/ (R6 +R7) = 15*60 / (15+60) =12 Ом
Теперь схема цепи примет вид, приведенный на рис. 9

Рис. 9
5. Находим эквивалентное сопротивление цепи, рис. 10:
R = R АД = R АВ +R ВС +R СД = 14+24+12=50 Ом
R АВ = R 1 =14 Ом
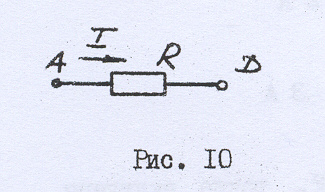
рис. 10
6. Для схемы, изображенной на рис. 10, нетрудно найти ток, потребляемый цепью, который одновременно является током неразветвленной части цепи.
На основании закона Ома
I=U/R=250/50=5A
Переходя от схемы к схеме в обратном порядке, найдём остальные токи. Так как схема, изображённая на рис. 9, представляет последовательное соединение участков АВ, ВС, СД, то на основании первого свойства этого вида соединения следует, что
I=IАВ=IВС=IСД=5А
(IАВ=I1)
7. Используя закон Ома, найдём падение напряжения на участках АВ, ВС и СД:
U АВ=U 1=IR 1 =5*14=70 В,
U ВС=U 1=IR ВС =5*24=120 В,
U СД=U 1=IR СД =5*12=60 В.
По ходу решения можно проверить правильность её решения. Так, на основании третьего свойства последовательного соединения следует, что
U=UАД=UАВ +UВС +UСД
Подставив значения напряжений участка, получаем:
U=UАВ +UВС +UСД = 770+120+60=250 В, что соответствует законному напряжению. Зная значения напряжений на участках ВС и СД, определим токи в ветвях (см. рис. 7).
8. На участке ВС резисторы R234 и R5 включены паралельно. На основании первого свойства этого вида соединения следует, что: UВС =U234 =U5 =120 В
Применяя закон Ома, находим токи ветвей участка ВС:
I234=UВС /R 234=120/60=2 А
I5=UВС /R 5=120/40=3 А
9. На участке СД резисторы R6 и R7 также включены паралельно, поэтому UСД=U6 =U7 =60 В
I6=UСД /R 6=60/15=4 А,
I7=UСД /R 7=60/60=1 А
На основании второго свойства паралельного соединения можно убедиться на этом этапе в правильности решения задачи, применив первый закон Кирхгофа. Из схемы (рис. 7) следует, что:
I=I1=I234+I5 и I=I1=I6+I7
Действительно:
I1=I234+I5 = 2+3 =5 А I=I1=5 А
I1=I6+I7 = 4+1=5 А
10. На рис. 8 видно, что на участке ВС верхняя ветвь представляет собой последовательное соединение резисторов R2 и R34, поэтому: I234=I2=I34 =2 А (смотри первое свойство данного вида соединений).
11. Для определения токов резисторов R3 и R4 предварительно найдем напряжение на резисторе R34 (рис.6), которое эквивалентно им, UСД=I34*R 34= 2*40=80 В
Так как резисторы R3 и R4 на реальной схеме (смотри рис.5) соединены паралельно U34=U3 =U4, то:
I3=U34/R 3 =80/50=1,6 А и I4=U34/R 4 =80/200=0,4 А
Проверка:
I2=I3+I4 =1,6+0,4=2 А (смотри первый закон Кирхгофа и второе свойство цепи с параллельным соединением)
12. При определении токов резисторов на каждом из них, кроме R2, было определено напряжение, что требуется также по условию задачи. Осталось найти напряжение на резисторе R2.
Это можно сделать двумя способами:
на основании закона Ома U2= I2*R 2 = 2*20 = 40 В
или на основании третьего свойства последовательного соединения. На участке ВС верхняя ветвь представляет собой последовательное соединение резисторов R2 и R34 (смотри рис. 6), поэтому UВС=U2 +U34,
отсюда U2=UВС –U34 = 120-80=40 В
Переходим к определению мощности, потребляемой цепью и каждым резистором в отдельности.
13. Мощность, потребляемая цепью P=U*I =250*5=1250 Вт. Мощности, потребляемые каждым резистором:
P1=U1*I1 =70*5=350 Вт
P2=U2*I2 =40*2=80 Вт
P3=U3*I3 =80*1,6=128 Вт
P4=U4*I4 =80*0,4=32 Вт
P5=U5*I5 =120*3=360 Вт
P6=U6*I6 =60*4=240 Вт
P7=U7*I7 =60*1=60 Вт
14. Проверим решение задачи на основании баланса мощностей, а
это значит, что:
P =P1+ P2+ P3+ P4+ P5+ P6+ P7 = 350+80+128+32+360+240+60=1250 Вт;
Вывод
Определение мощности цепей на основании баланса мощностей подтверждает значение мощности, полученной по формуле P=U*I
Значит задача решена правильно.
Примечание.
В рассмотренном примере пояснительный текст дан достаточно подробно для того, чтобы учащийся мог самостоятельно разбираться в решении задач, подобных примеру. При решении задач контрольной работы пояснения следует давать в обязательном порядке, но давать это более кратко.
Например, пункт 6 примера при оформлении может быть записан так:
6) Ток, потребляемый цепью, I = U/R = 250/50 = 5A;
Пункт 12:
12) Напряжение на резисторе R 2.
U2=I2*R 2 =2*20=40 В или
U2=UВС –U34 = 120-80=40 В и т.д.