Рассчитать и исследовать разветвленную электрическую цепь постоянного тока с использованием первого и второго законов Кирхгофа и методом контурных токов.
Для расчета разветвленной электрической цепи существенное значение имеет число ветвей и узлов в цепи.
Ветвью электрической цепи называется участок, состоящий только из последовательно соединенных элементов.
Вдоль ветви протекает неизменный ток, ветвь соединяет два узла.
Узлом электрической цепи называется точка соединения нескольких ветвей, в которой происходит разветвление тока.
В программе EWB понятие ≪узел≫ имеет другой смысл, – это любая точка схемы, имеющая потенциал, отличный от нуля и от потенциала других узлов. Так, одна ветвь в соответствии с теорией электрических цепей не имеет узлов, тогда как в программе EWB на одной ветви может быть несколько узлов рис.3.

Рис. 3. Пример понятия ≪узел≫ в программе EWB.
На (рис.3) слева показано, что в незаземленной цепи программа определяет три узла с разными потенциалами, заземленный участок узлом не считается, – (рис.1) справа. С точки зрения теории электрических цепей узел в приведенной схеме существует как раз на (рис.1) справа, в точке подключения заземления.
При обходе по соединенным в узлах ветвям можно получить замкнутый контур.
Замкнутый контур представляет собой замкнутый путь, проходящий по нескольким ветвям, при этом каждый узел в рассматриваемом контуре встречается не более одного раза.
Первый закон Кирхгофа применяется к узлам и формулируется следующим образом:
Алгебраическая сумма токов в узле равна нулю
 . (3)
. (3)
Алгебраической сумма называется потому, что должно быть учтено направление тока по отношению к узлу. Все токи, направленные к узлу входят в сумму с одним знаком, а направленные от узла – с противоположным. Первый закон Кирхгофа может быть сформулирован иначе:
Сумма токов, втекающих в узел, равна сумме токов вытекающих
из узла:
 . (4)
. (4)
Физический смысл первого закона Кирхгофа заключается в том, что в узлах электрической цепи не может происходить накопление заряда.
Второй закон Кирхгофа применяется к замкнутым контурам электрической цепи и формулируется следующим образом:
В любом замкнутом контуре алгебраическая сумма напряжений на
элементах контура равна сумме ЭДС в этом контуре
 (5)
(5)
В данном определении также подчеркивается, что сумма должна быть алгебраическая, это значит необходимо учесть знаки входящих в сумму напряжений и ЭДС. В замкнутом контуре ток может протекать только в одном направлении, поэтому должно быть выбрано направление протекания тока. После этого выполняется обход контура в выбранном направлении и падение напряжения на элементе или ЭДС источника считаются положительными, если ток через элемент или ЭДС совпадает с направлением обхода. В противном случае соответствующие напряжения и ЭДС суммируются с обратным знаком.
На основании законов Кирхгофа составляются уравнения для неизвестных токов в ветвях. Система полученных уравнений линейна, ее решение позволяет найти неизвестные токи в ветвях цепи. Результат расчета может быть проверен в программе EWB, подключением амперметров в разрыв соответствующих ветвей.
Варианты заданий
Принципиальные схемы для расчета приведены в таблице 4, варианты заданий и номинальные значения сопротивлений и ЭДС источников в таблице 5.
Таблица 4.
Принципиальные схемы
| № | схема | № | схема |

| 
| ||

| 
| ||

| 
| ||
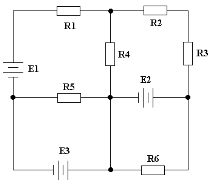
| 
| ||

| 
|
Таблица 5.
Параметры элементов схемы
| Ва- ри- ант | Схема | Значения сопротивлений, Ом | ЭДС источников, В | |||||||
| R1 | R2 | R3 | R4 | R5 | R6 | E1 | E2 | E3 | ||
Ход выполнения работы
1. Во вводной части сформулировать используемые теоретические закономерности;
2. Определить исходные данные для расчета: схему соединений, номиналы резисторов и ЭДС источников;
3. Ввести в схему условные обозначения узлов, контуров. Задать направление протекания токов и обхода контуров по часовой стрелки, начертить схему с указанными обозначениями;
4. Составить систему уравнений по первому и второму законам Кирхгофа;
5. Составить систему уравнений для контурных токов и уравнения для определения токов в ветвях;
5. Привести системы уравнений к стандартному виду, включив в каждое
уравнение все неизвестные;
6. Выбрать способ решения системы уравнений, выполнить решение, руководствуясь выбранным способом, ход решения со всеми ключевыми преобразованиями и пояснениями привести в отчете;
7. Если для некоторых токов получены отрицательные значения, начертить новую схему с исправленными направлениями токов;
8. Выполнить проверку решения подстановкой найденных неизвестных в исходные уравнения, в случае невыполнения условий проверки, повторить расчет и найти ошибку;
9. Собрать схему цепи в EWB. Измерить искомые токи с помощью включения амперметров в каждую ветвь исследуемой цепи и падения напряжений на всех сопротивлениях схемы;
10. Занести результаты расчета и измерений в отчет в виде таблицы 6;
Таблица 6.
Результаты расчетов исследований
| Метод расчета токов | Результаты расчета токов и напряжений в ветвях цепи. | Результаты измерения токов и напряжений в ветвях цепи. |
| Расчет токов и напряжений, с использованием 1 и 2 законов Кирхгофа | ||
| Расчет токов и напряжений, с использованием метода контурных токов |