Часть V
1. Найти все четные по значению элементы массива из n целых чисел. Вывести на экран значения элементов и их индекс.
2. Найти все элементы массива b(n), большие или равные 0. На экран вывести номера элементов, их значения и количество.
3. Найти сумму положительных элементов массива a(15).
4. Определить наибольший элемент массива a(n).
5. Вставить на k -ое место массива вещественных чисел элемент, равный наименьшему элементу массива.
6. В одномерном массиве целых чисел, содержащем 20 элементов, удалить k -ый элемент массива. Массив заполняется случайным образом числами от 0 до 50.
7. Найти сумму четных элементов массива целых чисел.
8. Найти произведение всех элементов массива целых чисел, меньших 0.
9. Заполнить массив по правилу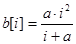 
10. Заполнить линейный массив по правилу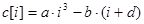 
11. Отсортировать по возрастанию линейный массив целых чисел a(n).
12. Дан линейный массив, содержащий положительные и отрицательные целые числа. Создать два новых массива, в одном из которых содержаться только положительные и нулевые, а в другом- только отрицательные элементы.
7. Вычислить значение функции 
, учитывая, что при х = 0 и х = 1 выражение не имеет смысла.
8. Возведите данное число в куб, если оно – чётное, и увеличите на 3, если оно – нечётное.
9. Вычислить значение функции: 
10. Составить алгоритм исследования квадратного уравнения
11. Написать программу решения уравнения 
для произвольного числа а.
12. Даны натуральные числа x, y, z, определяющие возраст трёх друзей. Из данных чисел напечатать те, которые обозначают “школьный” возраст, то есть от 7 до 16 лет.
13. Какое значение будет иметь переменная z после выполнения операторов:
|
|
z:= 0;
if x > 0 then if y > 0 then z:= 1 else z:=2;
при следующих значениях переменных x и y:
а) x = y= 1;
б) x = 1, y = -1;
в) x = -1, y = 1.
14. Три поросёнка Ниф – Ниф, Нуф – Нуф и Наф – Наф – нашли под дубом жёлуди. Каждый из них набрал себе приличный запас на зиму (дано три числа). Составить программу, которая определяла, кто из поросят поленился и набрал меньше всех.
15. Федя пытается протолкнуть в форточку размерами x см и y см свою голову диаметром не более d см. Удастся ли мальчику его эксперимент, или его голова застрянет.
16. Указать ошибки в следующих операторах:
а) if 1 < x < 2 then x:= x + 1; y:= 0;
else x:= 0; y:= y + 1;
б) if 1 < x and x < 2
then begin x:= x + 1; y:= 0 end;
else begin x:= 0; y:= y + 1 end;
17. Найти сумму цифр натурального трёхзначного числа k. Определить, является ли эта сумма чётным числом.
18. Найти первую цифру из дробной части действительного числа k. Определить, является ли эта цифра нечётным числом.
19. Дано четырёхзначное число N. Определить, делится ли это число на все свои цифры.
20. Вычислить следующие выражения при a = true, b = false
а) a or b and not a
б) (a or b) and not a
в) not a and b
г) not (a and b)
21. Чему равно значение логического выражения (a and not b) or c, если:
а) a = true, b = true, c = false;
б) все значения равны true;
в) все значения равны false;
г) a = true, b = false, c = true;
д) a = false, b = true, c = false.
Рекурсия
13. Пара кроликов каждый месяц даёт приплод – двух кроликов (самца и самку), от которых через два месяца уже получается новый приплод. Сколько пар кроликов будет через год, если в начале года мы имели одну пару только что родившихся кроликов?
|
|
14. Последовательность an строится так: a1 = 1, a2 = 3, an = an-1 - 2 * an-2 для каждого n> 2.
а) Найти первые 15 членов последовательности.
б) Найти сумму первых 15 членов этой последовательности.
15. Даны целые неотрицательные числа m и n. Вычислить так называемую «функцию Аккермана».
16. Функция F (n) определена для целых положительных чисел следующим образом:
Вычислить значения этой функции для n = 5, 6, 7, …, 20.
17. Найти сумму первых N членов арифметической прогрессии.
18. Задано N треугольников координатами своих вершин на плоскости. Напечатать номер треугольника с наибольшей площадью. Вычисление сторон и площадей организовать с помощью функций, воспользовавшись формулами длины отрезка и Герона.