Каким не может быть коэффициент корреляции?
a. 0,77
b. -0,34
c. 0,83
d. 1,01.
2. В каком случае выполняется соотношение для коэффициента детерминации и коэффициента корреляции 
?
a. в линейной модели;
b. в нелинейной модели;
c. как в линейной, так и в нелинейной
3. Оценки параметров модели называются эффективными, если:
a. математическое ожидание оценок параметров совпадает с истинными значениями этих параметров;
b. оценки параметров сходятся по вероятности к истинным значениям параметров;
c. в классе линейных оценок оценки параметров модели имеют минимальные дисперсии.
4. Коэффициент парной корреляции изменяется в пределах:
a. от 0 до 1;
b. от -1 до 0;
c. от -1 до 1.
5. Оценку параметра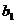 
парной линейной регрессии 
можно найти по формуле:
а) 
б) 
в) 
6. В регрессии: Y = 0, 1 + 4х тангенс угла наклона равен:
а) х б) y в) 4 г) 0,1
. 7. С учетом соотношения между заработной платой (в грн) –у и образованием (в годах) –х, у = 12,201 + 525 х, человек, который учился дополнительно один год, может ожидать такую дополнительную оплату: а)12,201 б)525 в)24,402 г)1,050
8. Критерий Стьюдента используется для оценки статистической значимости:
a. параметров модели;
b. коэффициента корреляции;
c. как параметров модели, так и коэффициента корреляции.
9. Коэффициент детерминации измеряет:
a. независимой переменной;
b. наклон линии регрессии;
c. всегда равен 1;
d. пересечение линии регрессии; д) общую вариацию независимой переменной, которая объясняется регрессией.
10. Значение выборочного коэффициента парной корреляции между факторами х и у определяется по формуле:
а.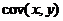 
b. 
c. 
11. Статистический анализ модели (статистическое оценивание ее параметров) относится к этапу:
- априорному;
- информационному;
- идентификации;
- верификации.
12. Линейные регрессионные модели, остатки которых не сохраняют постоянного уровня величины дисперсии при переходе от одного наблюдения к другому, называют моделями с:
a. гомоскедастичными остатками;
b. клонированными остатками;
c. гетероскдастичными остатками;
d. перпендикулярными остатками.
13. Временной ряд является нестационарным, если:
a. среднее значение его членов постоянно:
b. его случайная составляющая зависит от времени;
c. его члены не зависят от времени;
d. его неслучайная составляющая зависит от времени.
13. Теснота статистической связи между переменной и объясняющими переменными измеряется:
- моментом связи;
- коэффициентом детерминации;
- числом Блаттера;
- статистическим ансамблем.
14. Если регрессионные остатки в эконометрической модели статически взаимозависимы, то ее называют моделью с:
- автокоррелированными остатками;
- гомоскедастичными остатками;
- параллельными остатками;
- картезианскими остатками.
15. Линеаризация нелинейной модели регрессии может быть достигнута:
- отбрасыванием нелинейных переменных;
- перекрестной суперпозицией переменных;
- преобразованием анализируемых переменных;
- сглаживанием переменных.
Одно из условий идентифицируемости системы одновременных уравнений (СОУ) состоит в том, что
- переменные являются коллинеарными;
- число уравнений равно числу анализируемых эндогенных переменных;
- переменные являются компланарными;
- число уравнений меньше числа анализируемых эндогенных переменных.