Рисунок 1.11. - Модель источника с компенсационным стабилизатором напряжения (Uвх = 187 В Rн = 5 Ом)
Рисунок 1.12. - Модель источника с компенсационным стабилизатором напряжения (Uвх = 220 В Rн = 5 Ом)
Рисунок 1.13. - Модель источника с компенсационным стабилизатором напряжения (Uвх = 242 В Rн = 5 Ом)
Рисунок 1.14. - Модель источника с компенсационным стабилизатором напряжения (Uвх = 187 В Rн = 4,5 Ом)
Активные фильтры
Благодаря тому, что реактивное сопротивление конденсатора, равное
Zс = – j/wc, зависит от частоты, с помощью конденсаторов и резисторов можно строить частотно-зависимые делители напряжения, которые будут пропускать только сигналы нужной частоты, а все остальные подавлять – пассивные фильтры.
Активными называются фильтры, использующие для формирования частотных характеристик как пассивные, так и активные (усилительные) элементы, что дает возможность усиливать сигнал, лежащий в полосе пропускания[1,3]. Активные фильтры классифицируются на фильтры низких частот (ФНЧ), пропускающие сигналы с частотой от f = 0 до некоторой частоты среза f = f0; фильтры высоких частот (ФВЧ), пропускающие сигналы с частотой от f = f0 до f ® ¥; полосовые (ПФ), пропускающие сигналы в диапазоне частот от f1 до f2, и режекторные фильтры (РФ), не пропускающие сигналы в узком диапазоне частот от f1 до f2. На частоте среза f0 сигнал уменьшается до 0,7 К0, что соответствует 3 д Б.
Типовые ЛАЧХ перечисленных фильтров приведены на рис.2.1.
Электрические фильтры аналитически принято описывать передаточными функциями. Передаточные функции простейших фильтров представляют собой уравнения первого порядка, поэтому и фильтры называются фильтрами первого порядка. Коэффициент усиления у них уменьшается с частотой на 20 д Б/дек. Такие фильтры просты, но имеют малую крутизну спада ЛАЧХ, что свидетельствует о плохих избирательных свойствах. Для улучшения избирательности нужно повышать порядок передаточных функций за счет введения дополнительных RC-цепей или последовательного включения идентичных активных фильтров. На практике наиболее часто используют операционные усилители (ОУ) с цепями обратных связей (ОС), работа которых описывается уравнениями второго порядка – фильтры второго порядка. Коэффициент усиления у них уменьшается с частотой на 40 д Б/дек. При необходимости повысить избирательность системы отдельные фильтры второго порядка включают последовательно.
|
|
Рисунок 2.1. ЛАЧХ фильтров: а) ФНЧ; б) ФВЧ; в) ПФ; е) РФ
Рассмотрим наиболее часто используемые схемы активных фильтров. На рис. 2.2 приведена структурная схема фильтра с многопетлевой обратной связью, позволяющая реализовать фильтры нижних и верхних частот второго порядка (n = 40 д Б/дек). Каждый пассивный двухполюсный элемент в этой схеме может быть либо резистором, либо конденсатором [10].
 |
Рисунок 2.2 Структурная схема активного фильтра второго порядка
Передаточная функция для данной схемы имеет вид
. (2.1)
Для того чтобы схема осуществляла фильтрацию низких частот, передаточную функцию (2.1) необходимо привести к передаточной функции, соответствующей низкочастотному звену второго порядка:
, (2.2)
где w0 = 2pf0, H = k0, a – коэффициент затухания.
Сравнивая выражения (2.1) и (2.2), можно заметить, что для того чтобы числитель не был функцией р, в качестве Y1 и Y4 должны использоваться резистивные проводимости, для того чтобы получить член с р2 в знаменателе, в качестве Y3 и Y5 должны использоваться емкостные проводимости, для того чтобы получить в знаменателе член, независимый от р, в качестве Y2 должна использоваться резистивная проводимость. Итак, однозначно определяются пассивные элементы:
|
|
Схема полученного фильтра-ФНЧ приведена на рис.2.3. Передаточная функция имеет вид:
. (2.3)
| Рисунок 2.3. Схема ФНЧ второго порядка | Рисунок 2.4. Схема ФВЧ второго порядка |
Сравнивая выражения (2.3) и (2.2), получаем соотношения, необходимые для расчета фильтра:
. (2.4)
В том случае, если С1 = С2 = С и R2 = R3 = R, последние формулы упрощаются:
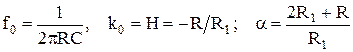. (2.5)
Для получения максимально плоской характеристики задают a= 
, при этом R1 ¹ R2 ¹ R3. Чтобы не решать довольно сложную систему алгебраических уравнений, можно привести ее решение в общем виде. Для этого, задавшись значением емкости С2, находят вспомогательный коэффициент k=2pf0C2 и через него, а также через величины f0, a и H выражают величины остальных элементов схем фильтра:
(2.6)
Если поменять местами емкости и сопротивления в схеме на рис.2.3, то получим фильтр верхних частот, схема которого приведена на рис.2.4. Передаточная функция для этой схемы:
. (2.7)
Сравнивая последнее выражение с выражением для высокочастотного звена второго порядка
, (2.8)
получим
. (2.9)
В том случае, если С2 = С3 = С и R1 = R2 = R, получим
. (2.10)
Для реализации максимально плоской характеристики (a= ) следует задаться значениями С1 = С3 = С, вычислить 
и найти остальные элементы фильтра по следующим формулам:
|
|
. (2.11)
Для того чтобы параметры OY не оказывали влияния на работу фильтров, номиналы резисторов в схемах должны удовлетворять следующим неравенствам:
и частота единичного усиления OY должна быть 
для ФНЧ и
для ФВЧ.
Номиналы емкостей, с одной стороны, должны быть значительно больше паразитных емкостей в схеме фильтра, с другой стороны, эти емкости не должны быть слишком большими, так как при этом увеличиваются габариты устройства и потери в конденсаторах.
Задание
Спроектировать и исследовать на компьютере активные фильтры нижних и верхних частот второго порядка с максимально плоской характеристикой.
Дано: f0 – частота среза; К0 – коэффициент усиления в полосе пропускания; 
– коэффициент затухания, n = 40 д Б/дек – наклон ЛАЧХ в полосе ограничения.
Исходные данные для расчета ФНЧ и ФВЧ помещены в таблицах 2.1 и 2.2. Вариант определяется двумя цифрами шифра зачетки. Цифра единиц указывает номер исходных данных в табл. 2.1, цифра десятков — в табл. 2.2.
Таблица 2.1.
| № варианта | ||||||||||
| f0, [кГц] |
Таблица 2.2.
| № варианта | ||||||||||
| К0 |
2.2. Методика расчета ФНЧ и ФВЧ второго порядка и исследования
на компьютере
I. Расчет ФНЧ второго порядка (схема, рис. 2.3.).
1. Задаться величиной емкости С2 (не более 2200рФ, значение брать по ряду Е12) и найти значение вспомогательного коэффициента k=2pf0C2.
2. Рассчитать значения всех элементов схемы фильтра: С1, R1, R2 и R3 по формулам (2.6). Полученные величины округлять по ряду Е12.
3. Проверить значения частоты среза f0 и усиления k0 по формулам
Расчетные значения не должны отличаться от заданных более чем на ±10%.
4. Рассчитать коэффициент усиления k0 в децибелах для построения ЛАЧХ, k0доб = 20lg k0.
5. Определить параметры операционного усилителя – ОY для выбора его по справочнику или задания этих значений в модели ОY пакета EW.
RвыхОY £ Rmin/10,
RвхОY ³ 10Rmax,
fТОY ³ k0f0,
где Rmin и Rmax – номиналы резисторов в схеме рассчитанного фильтра,
fТОY – частота единичного усилителя ОУ.
6. Набрать на компьютере (пакет EW) схему рассчитанного ФНЧ с подключением источника сигнала и плоттера (рис.2.5). Боде-плоттер генерирует собственный спектр частот, который задается при настройке.
7. Исследовать работу ФНЧ.
Для получения наглядной ЛАЧХ на плоттере необходимо его настроить после запуска схемы. Выставить режимы MAGNITUDE и LOG. Начальные значения (I) по вертикали и горизонтали можно взять 0 дБ и 1 кГц, а конечные для вертикали K > 20 lg k0, для горизонтали F > f0. Если вид ЛАЧХ соответствует исследуемому фильтру, то необходимо определить параметры k0, д Б и f0. Значения k и f выводятся на информационное поле плоттера при перемещении курсора, расположенного в начале горизонтальной шкалы.
8. Сделать распечатки схемы ФНЧ с показаниями плоттера для f< f0 (К должно быть =Ко) и для К=Ко-3дб (f должно быть=fо).Если полученные значения на плоттере Ко(дб) и fо не отличаются от заданных больше, чем на 15%, то ФНЧ спроектирован верно.
9. Выводы.
Рисунок 2.5. Схема ФНЧ второго порядка
Рисунок 2.6. Схема ФВЧ второго порядка
II. Расчет ФВЧ второго порядка (схема рис. 2.4.)
1. Задать значение емкости конденсаторов С1 = С3 = С (не более 2200 рФ) и найти значение вспомогательного коэффициента k = 2pf0C.
2. Рассчитать значения всех элементов схемы фильтра: С2, R1, R2 по формулам (2.11). Полученные величины округлить по ряду Е12.
3. Проверить значения частоты среза f0 и усиления k0 по формулам
.
Расчетные значения не должны отличаться от заданных более чем на ±10%.
4. Рассчитать коэффициент усиления k0 в децибелах для построения ЛАЧХ, k0, д Б = 20 lgk0.
5. Определить параметры операционного усилителя, так же как для ФНЧ.
6. Набрать на компьютере (пакет EW) схему рассчитанного ФВЧ с подключением плоттера (рис.2.6).
7. Исследовать работу ФВЧ аналогично ФНЧ.
8. Сделать распечатки схемы ФВЧ с показаниями плоттера для f> fо (К должно быть равно Ко) и для К = Ко-3дб (f должно быть равно fо).
9. Выводы.