Приложение А Техническое задание

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

 

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫПО КУРСУ

ТЕОРИЯ АЛГОРИТМОВ И ВЫЧИСЛИТЕЛЬНЫХ ПРОЦЕССОВ

 

(для студентов специальности 7.080403 «Программное обеспечение вычислительной техники и автоматизированных систем», «Компьютерный эколого-экономический мониторинг»)

 

 

Рассмотрено на заседании кафедры

Прикладной математики и информатики

Протокол № __9__ от «4»_02______2009г.

 

 

Донецк 2009

Методические указания к выполнению курсовой работы по курсу «Теория алгоритмов и вычислительных процессов» (для студентов специальностей «Программное обеспечение вычислительной техники и автоматизированных систем», «Компьютерный эколого-экономический мониторинг»)

Сост.: Коломойцева И. А., Назарова И.А.

 

Тема курсовой работы:

«Построение аналитических моделей алгоритмов и

Оценка их сложности

 

Задание на курсовую работу:

 

1. Рекурсивные функции

Разработать алгоритм вычисления в виде рекурсивной функции. Проверить модель алгоритма на множестве тестовых примеров. Определить к какому классу рекурсивных функций принадлежит : примитивно-рекурсивна, частично рекурсивна или общерекурсивна.

 

2. Машины Тьюринга

2. 1.Описать системой команд, функциональной таблицей и диаграммой переходов работу машины Тьюринга, реализующую заданный вариантом алгоритм. Начальная и конечная конфигурации стандартны. Проверить модель алгоритма на множестве тестовых примеров. Привести последовательности конфигураций машины Тьюринга для различных тестовых исходных слов.

2.2. Построить машину Тьюринга, вычисляющую функцию из задания №1 “Рекурсивные функции”. Машину Тьюринга представить как композицию элементарных МТ, выполняющих операции: копирование аргумента, сложение, умножение, арифметическое вычитание, нахождение целой части и остатка от деления, сравнения чисел, выделение аргумента. Недостающие элементарные МТ описать любым известным способом.

2.3. Определить машину Тьюринга, распознающую заданный язык. Программно реализовать эту машину и построить график ее временной сложности T(n) (для n, требующих 3-5 мин. счета).

 

3. Нормальные алгоритмы Маркова

Составить нормальный алгоритм Маркова над алфавитом А. На конкретных примерах исходных слов продемонстрировать работу составленных алгоритмов.

 

Варианты заданий к заданию №1

1. Сумма всех делителей числа .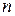

2. Количество делителей числа .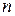

3. Количество нулей в двоичной записи .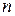

4. Сумма цифр в двоичной записи .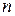

5. Количество взаимно-простых с 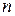чисел,

6. Максимум из двух чисел и ,

7. Минимум из двух чисел и ,

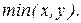
8. Модуль разности двух чисел и ,

9. Максимальная цифра в 8-ричной записи числа .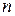

10. Минимальная цифра в 8-ричной записи числа .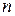

11. Количество четных цифр в 8-ричной записи числа .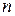

12. Количество нечетных цифр в 8-ричной записи числа .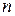

13. Сумма простых делителей числа .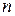

14. Количество простых делителей числа .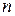

15. Количество простых чисел,

16. Количество чисел, являющихся полными квадратами,

17. Сумма чисел, являющихся степенью двойки,

18. Максимальная цифра в 16-ричной записи числа .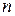

19. Минимальная цифра в 16-ричной записи числа .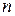

20. Ближайшее к 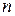простое число.

21. Произведение делителей числа .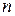

22. Произведение простых делителей числа .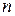

23. Произведение взаимно-простых с 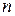чисел,

24. Наименьшее общее кратное двух чисел, ,

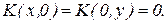
25. Наибольший общий делитель двух чисел,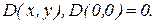

26. Целая часть от деления на , или .

27. Остаток от деления на ,

28. “Ступенька”: .

29. Функция, отличная от нуля в конечном числе точек.

30. Номер наибольшего простого делителя числа

31. Функция .

 

Варианты заданий к заданию 2.1

 

1. Реализовать функцию арифметическое вычитание в унарном коде.

2. Реализовать функцию выбор максимального из двух чисел над числами в унарном коде.

3. Реализовать функцию над числами в унарном коде.

4. Реализовать функцию над числами в унарном коде.

5. Реализовать функцию 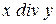над числами в унарном коде.

6. Реализовать функцию 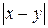над числами в унарном коде.

7. Реализовать функцию выбор аргумента 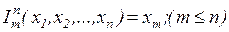над числами в унарном коде.

8. Реализовать вычисление предиката X>Y в унарном коде с сохранением (восстановлением) исходных данных.

9. Реализовать вычисление предиката X=Y в унарном коде с сохранением (восстановлением) исходных данных.

10. Реализовать вычисление предиката “x - четное число” в двоичном коде.

11. Реализовать алгоритм в алфавите 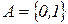, меняющий местами первую и последнюю буквы слова.

12. Реализовать алгоритм над алфавитом 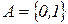, меняющий местами первый ноль и последнюю единицу.

13. Реализовать операцию копирование в алфавите , то есть получить из слова слово .

14. Реализовать алгоритм над алфавитом 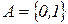, который выдает единицу, если в исходном слове только парные нули и ноль в противном случае.

15. Реализовать алгоритм в алфавите 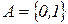, который переставляет буквы в слове так, чтобы сначала шли все нули, потом – единицы.

16. Реализовать алгоритм, конструирующий в алфавите 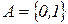слова вида 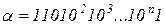, где 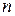- произвольное натуральное число.

17. Реализовать алгоритм, реализующий функцию циклический сдвиг двоичного числа на одну ячейку.

18. Реализовать алгоритм в алфавите , анализирующий последовательность цифр в слове и выдающий «+», если цифры образуют неубывающую последовательность, и «–» в противном случае.

19. Реализовать выделение подстроки, заключенной между двумя символами (первая пара) в алфавите . Если последовательность отсутствует на ленте, стереть все.

20. В слове в алфавите 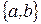стереть все, кроме 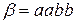. Если такой последовательности нет, все стереть.

21. Реализовать алгоритм над алфавитом 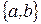, переставляющий буквы в обратном порядке.

22. Реализовать предиката «в слове a в алфавите есть пара букв ‘ yy ’ ».

23. Реализовать алгоритм в алфавите , производящий в слове a алфавита замену всех вхождений буквы а на букву б.

24. Реализовать алгоритм в алфавите 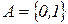для вычисления логической функции , где x,y,z принимают значение 0 или 1.

25. Реализовать алгоритм в алфавите 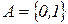для вычисления логической функции , где x,y,z принимают значение 0 или 1.

 

Варианты к заданию 2.3

 

1. L = {0ⁿ1ⁿ2ⁿ ên≥1}

2. L = {a³ⁿ ên≥1}

3. L = {a⁴ⁿ ên≥1}

4. L = {a⁵ⁿ ên≥1}

5. L = {a⁶ⁿ ên≥1}

6. L = {a⁵ⁿb⁷ⁿ ên≥1}

7. L = {wÎ{0, 1}^* │w не содержит 3-х идущих подряд единиц}

8. L = {wÎ{0, 1}^* │w не содержит 2-х идущих подряд нулей}

9. L = {wÎ{0, 1}^* │w не содержит комбинации ‘0101’}

10. L = {wÎ{0, 1}^* │w не содержит комбинации ‘1010’}

11. L = {wÎ{0, 1}^* │w не содержит 2-х идущих подряд единиц}

12. L = {aⁱb^jc^k ê1≤i<j<k}

13. L = {aⁱb^jc^k êi=jÚj=k && i,j,k≥1}

14. L = {aⁱb^jc^k ê1≤i=j & k≥1}

15. L = {aⁱb^jc^k ê1≤i=j & k≥1 & i¹k}

16. L = {aⁱb^jc^k ê1≤i=k & j≥1}

17. L = {aⁱb^jc^k ê1≤i=k & j≥1 & i¹j}

18. L = {aⁿ ên≥1}È {bⁿ ên≥1}

19. L = {a^mbⁿ êm,n≥1}

20. L = { a^mbⁿ êm,n≥1}È {cⁿ ên≥1}

21. L = { wcw^R│wÎ{0, 1}^*}

22. L = { ww^R│wÎ{0, 1}^*}

23. L = {aⁱb^j êi≥1 & j>i}

24. L = {aⁱb^j êj≥1 & i>j}

25. L = {aⁱb^jc^k êi¹j & j¹k & i, j, k ≥1}

26. L = {aⁱb^jc^k êi¹j & i¹k & j¹k& i, j, k ≥1}

27. L = {aⁱb^jc^k êi,j≥1 & k≥max{i,j}}

28. L = { wcw^Rcw│wÎ{0, 1}^*}

29. L = { wcw^Rcwcw^R│wÎ{0, 1}^*}

30. L = { ww│wÎ{0, 1}^*}

31. L = { www│wÎ{0, 1}^*}

32. L = { wwww│wÎ{0, 1}^*}

33. L = { ww^Rw│wÎ{0, 1}^*}

34. L = { ww^Rw^R│wÎ{0, 1}^*}

35. L = { ww^Rww^R│wÎ{0, 1}^*}

36. L = {wÎ{a, b}^* │w содержит ровно вдвое больше символов a, чем b}

37. L = {wÎ{a, b, c}^* │w состоит из одинакового числа символов a,b и c}

38. L = {(ab)ⁿcⁿ(dd)ⁿ ên≥1}

39. L = {wÎ{a, b}^* │w состоит из одинакового числа символов a и b}

40. L = {aⁿb^m ên≤m≤2n}

41. L = { vcw│w, vÎ{0, 1}^* & v¹w}

42. L = { w₁cw₂c... cw_mccw_i^R│1≤i≤m & "_1≤j≤m (w_jÎ{0, 1}^*)}

43. L = { w₁cw₂cw₂^Rcw₁^R│w₁w₂Î{a, b}^*) & w₁ ¹w₂}

44. L = { a^│w│bw│wÎ{a, b}^*)}

45. L = { vcwcv│w, vÎ{0, 1}^* & v¹w}

46. L = { vcwcw^R│w, vÎ{0, 1}^* & v¹w}

47. L = {wÎ{0, 1}^* │w состоит из одинакового числа нулей и единиц}

48. L = { vcwcv^R│w, vÎ{0, 1}^* & v¹w}

49. L = {aⁿbⁿcⁿ(dab)ⁿ ên≥1}

50. L = {aⁿb^mcⁿ êm, n≥1 & n¹m}

51. L = {aⁿb^mcⁿ êm, n≥1 & n≤m≤2n}

52. L = { a^│w│b^│w│-1cw│wÎ{a, b}^* & │w│>=1}

53. L = { a^│w│b^│w│/2cw│wÎ{a, b}^*)}

54. L = {0ⁿ1ⁿ0²ⁿ1²ⁿ ên≥1}

55. L = {(01)ⁿc(10)ⁿ ên≥1}

56. L = {0ⁿ1^m êm,n≥1 & m¹n & m¹3n}

57. L = {1ⁿ01²ⁿ01³ⁿ ên≥1}

58. L = {(1010)ⁿc(0101)ⁿ ên≥1}

59. L = {(abcd)ⁿ(acdb)ⁿ ên≥1}

60. L = {wÎ{0, 1}^* │если w содержит четное количество нулей, то единиц в w должно быть в два раза больше, чем нулей}

61. L = {wÎ{0, 1}^* │если w содержит нечетное количество единиц, то нуль в w должен встретиться 1 раз}

62. L = { w₁сw₁^Rсw₂сw₂^R│w₁, w₂Î{0, 1}^*}

63. L = { w₁сw₂сw₁^Rсw₂^R│w₁, w₂Î{0, 1}^*}

64. L = { wcw^Rcv│w, vÎ{0, 1}^* & v¹w & │w│=2n & │v│=3n & n≥0}

65. L = { wcvcv^R│w, vÎ{0, 1}^* & v¹w & │w│=│v│=2n & n≥0}

66. L = { wcv│w, vÎ{0, 1}^* & v¹w & │w│=2k & │v│=2n & k, n≥0}

67. L = { wcv│w, vÎ{0, 1}^* & │w│=2k & │v│=2n+1 & k¹n & k, n≥0}

68. L = {0ⁿ1^m êm,n≥1 & m¹4n & m¹n & m¹3n}

69. L = {aⁿb²ⁿc⁴ⁿ ên≥1}

70. L = {(ad)ⁿ(cb)²ⁿ ên≥1}

71. L = {wÎ{0, 1, 2}^* │w должно содержать одинаковое количество нулей и единиц, а двоек должно быть в два раза больше}

72. L = {aⁿbc⁵ⁿab³ⁿ ên≥1}

73. L = { vcv^Rcwcv^R│w, vÎ{0, 1}^* & v¹w & │w│=│v│=2n+1 & n≥0}

74. L = { a^│w│b^2│w│cw│wÎ{a, b}^*)}

75. L = { ww^Rw^R│wÎ{a, b, c}^*}

76. L = {wÎ{0, 1, 2}^* │w должно содержать в два раза больше единиц, чем нулей, а двоек - в три раза больше, чем единиц}

77. L = {aⁱb^jc^k êi, k≥1 & j=min(i, k) }

78. L = {aⁱb^jc^k êi, k≥1 & j=max(i, k) }

79. L = {aⁱb^jc^k êj, k≥1 & i=min(j, k) }

80. L = {aⁱb^jc^k êj, k≥1 & i=max(j, k) }

81. L = {aⁱb^jc^k êi, j≥1 & k=min(i, j) }

82. L = {aⁱb^jc^k êi, j≥1 & k=max(i, j) }

83. L = {(ad)ⁿ(cb)ⁿ ên≥1}

84. L = {(ad)²ⁿ(cb)ⁿ ên≥1}

85. L = {aⁱb^jc^k êi>j>k ≥1}

86. L = {(ab)ⁿ(ba)ⁿ ên≥1}

87. L = {wÎ{0, 1, 2}^* │w должно содержать в два раза больше единиц, чем нулей, а двоек - в три раза больше, чем нулей}

88. L = { ww^Rw│wÎ{a, b, c}^*}

89. L = { www│wÎ{a, b, c}^*}

90. L = { ww^R│wÎ{a, b, c}^*}

91. L = { ww│wÎ{a, b, c}^*}

92. L = { wwww│wÎ{a, b, c}^*}

93. L = { ww^Rww^R│wÎ{a, b, c}^*}

94. L = { ww^Rww│wÎ{a, b, c}^*}

95. L = { ww^Rw^Rw^R│wÎ{a, b, c}^*}

96. L = { www^Rw│wÎ{a, b, c}^*}

97. L = { wwww^R│wÎ{a, b, c}^*}

98. L = {aⁿb⁴ⁿc²ⁿ ên≥1}

99. L = {aⁿb⁵ⁿc³ⁿ ên≥1}

100. L = {aⁿb³ⁿc²ⁿ ên≥1}

 

Индивидуальные варианты к заданию №3

 

1. Реализовать алгоритм, выполняющий замену в слове в алфавите каждого символа на символ .

2. Реализовать алгоритм, выполняющий перестановку в слове в алфавите букв таким образом, чтобы сначала стояли все нули, а затем все единицы.

3. Составить нормальный алгоритм, преобразующий исходную строку в алфавите в строку, в которой буквы расположены в алфавитном порядке.

4. Реализовать алгоритм, выполняющий над числами в унарном коде.

5. Реализовать алгоритм, выполняющий 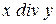над числами в унарном коде.

6. Реализовать алгоритм, выполняющий 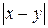над числами в унарном коде.

7. Реализовать алгоритм, вычисляющий арифметическое вычитание в унарном коде.

8. Реализовать функцию выбор аргумента 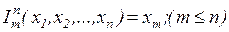над числами в унарном коде.

9. Реализовать вычисление предиката X=Y в унарном коде с сохранением (восстановлением) исходных данных.

10. Реализовать вычисление предиката X>Y в унарном коде с сохранением (восстановлением) исходных данных.

11. Реализовать алгоритм в алфавите 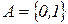, меняющий местами первую и последнюю буквы слова.

12. Реализовать алгоритм над алфавитом 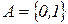, меняющий местами первый ноль и последнюю единицу.

13. Реализовать операцию копирование в алфавите , то есть получить из слова слово .

14. Реализовать алгоритм над алфавитом 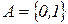, который выдает единицу, если в исходном слове только парные нули и ноль в противном случае.

15. Реализовать алгоритм в алфавите 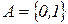, который переставляет буквы в слове так, чтобы сначала шли все нули, потом – единицы.

16. Реализовать алгоритм над алфавитом 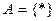, исключающий в слове последнюю звездочку.

17. Реализовать алгоритм, реализующий функцию циклический сдвиг двоичного числа на одну ячейку.

18. Реализовать алгоритм в алфавите , анализирующий последовательность цифр в слове и выдающий «+», если цифры образуют неубывающую последовательность, и «–» в противном случае.

19. Реализовать алгоритм над алфавитом 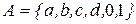, который выдает 1, если исходное слово содержит комбинацию baccd, и 0 - в противном случае.

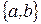20. Реализовать алгоритм, выполняющий следующие действия. В слове в алфавите стереть все, кроме 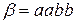. Если такой последовательности нет, все стереть.

21. Реализовать алгоритм над алфавитом 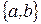, переставляющий буквы в обратном порядке.

22. Реализовать алгоритм над алфавитом , который выдает 1, если в исходном слове содержатся только парные нули, и 0 - в противном случае.

23. Реализовать алгоритм над алфавитом , который выдает «да », если в исходном слове четное количество y -ков, и «нет» в противном случае;

24. Реализовать алгоритм над алфавитом 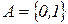, выдающий в результате столько единиц, сколько нулей в исходном слове.

25. Реализовать алгоритм над алфавитом , выделяющий часть слова расположенную между первой парой звездочек.

 

 

СОДЕРЖАНИЕ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ

 

Титульный лист

Реферат

Содержание

Введение

1. Описание формальной модели алгоритма на основе рекурсивных функций

2. Описание аналитической модели алгоритма в виде элементарных машин Тьюринга и композиции МТ

3. Разработка аналитической и программной модели алгоритма для распознающей машины Тьюринга

3.1 Формальное определение машины распознающей Тьюринга

3.2 Протоколы работы машины Тьюринга (на двух словах языка и двух словах, не принадлежащих языку)

3.3 Программная модель машины Тьюринга

3.4 Протоколы работы машины Тьюринга, построенные программно (на двух словах языка и двух словах, не принадлежащих языку)

3.5 Расчет временной сложности (график функции временной сложности)

4. Разработка аналитической модели алгоритма с использованием нормальных алгоритмов Маркова

Выводы

Перечень ссылок

Приложение А Техническое задание