Учебник: Алгебра: Учеб.для 8 кл. общеобразоват. учреждений \ Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. – 6-е изд., дораб. – М.: Просвещение, 1999. – 225 с.Глава IV.
Тип урока: обобщения и систематизация.
Учебная задача урока:
1) Систематизация и обобщение изученного материала по теме: «Квадратное уравнение и его решение».
2) Совершенствование умений и навыков учащихся по решению квадратных уравнений.
Диагностируемые цели:
В результате ученик
знает:
1. Понятие квадратного уравнения;
2. Виды квадратных уравнений и способы их решения;
3. Метод выделения полного квадрата;
4. Теорему Виета и её доказательство;
5. Теорему, обратную теореме Виета;
6. Понятие дискриминанта;
7. Формулы для вычисления корней квадратного уравнения;
8. Способ разложения квадратного трёхчлена на множители.
умеет:
1. Выделяет квадратное уравнение из других;
2. Решать квадратное уравнение методом выделения полного квадрата;
3. Решать квадратные уравнения различных видов, в том числе с помощью формул;
4. Применять теорему Виета и обратную ей;
5. Раскладывать квадратный трехчлен на множители;
6. Применять различные способы преобразования уравнений, сводящихся к квадратным уравнениям;
7. Решать задачи с помощью квадратного уравнения;
8. Решать простейшие системы с уравнениями второй степени.
понимает:
1. Что способ решения квадратного уравнения зависит от его вида;
2. Роль дискриминанта в исследовании числа корней квадратного уравнения;
3. Смысл теоремы Виеты и обратной ей;
4. Основные этапы процесса составления квадратного уравнения при решении текстовых задач;
5. Смысл разложения квадратного уравнения на множители;
6. Какие существуют типы текстовых задач, решение которых сводится к составлению квадратного или дробно-рационального уравнения.
Методы обучения: репродуктивный, частично-поисковые, метод УДЕ.
Форма работы: фронтальная.
Средства обучения: мел, доска, учебник, листы с заданиями, канва-таблица, презентация.
Структура урока:
1. Мотивационно-ориентировочный этап (5мин.),
2. Содержательный этап (30 мин.),
3. Рефлексивно-оценочный этап (5 мин.).
Ход урока:
1. Мотивационно-ориентировочный этап.
Актуализация.
На протяжении всего урока заполняется канва-таблица.
На доске записаны задания. Работа идет устно со всем классом.
№1. Какие из данных уравнений являются а) квадратными? б) уравнения, сводящиеся к квадратным? в) неполными квадратными? г) приведенными квадратными?
1) 
2) 
3) 
4) 
5) 
6) 
Ответ: а) 1, 2, 4, 6; б) 5; в) 1, 6; г) 2
-Сформулируйте определение квадратного уравнения.
(Квадратным уравнением называется уравнение  , где
, где  - заданные числа,
- заданные числа,  ,
,  - неизвестное.)
- неизвестное.)
(в канву-таблицу1 записывается определение квадратного уравнения).
-Какие существуют виды неполных квадратных уравнений? Каковы способы их решения?
1)  , а ≠0
, а ≠0
 ,
,
 ,
,
а)  , тогда
, тогда 
б)  , тогда
, тогда  ,
,  или
или  .
.
2)  а ≠0
а ≠0
Раскладываем левую часть на множители:
 , откуда
, откуда  ,
, 
Выполняются соответствующие записи в канве-таблице1.
-Какое квадратное уравнение называется приведённым?
(Квадратное уравнение вида  называется приведенным)
называется приведенным)
Делаются соответствующие записи в канве-таблице1: полные уравнения делятся на уравнения, у которых старший коэффициент ¹ 1 и приведённые.
-Ребята, любое ли полное квадратное уравнение можно сделать приведенным? Как? (да, поделить на старший коэффициент).
№2. Сколько корней имеет уравнение  , если а)
, если а)  ; б)
; б)  ; в)
; в)  ?
?
Ответ: а) один корень; б) нет действительных корней; в) два различных корня.
-Как вы это определили? (нашли дискриминант  ).
).
-итак, если  , уравнение имеет один корень. Если
, уравнение имеет один корень. Если  , то уравнение не имеет действительных корней. Если
, то уравнение не имеет действительных корней. Если  , то два действительных корня.
, то два действительных корня.
Делаются соответствующие записи в канву-таблицу1.
№3. Решить уравнение: а)  ; б)
; б)  ; в)
; в) 
Решение:
а)  ,
,
-Ребята, вспомните формулу корней квадратного уравнения общего вида. ( ). Запишите её в канву-таблицу.
). Запишите её в канву-таблицу.
 ,
,
 ,
,  .
.
б) 
-Ребята, вспомните формулу корней с четным средним коэффициентом. (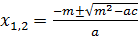 )
)

Запишите формулу корней с четным средним коэффициентом в канву-таблицу. (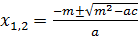 )
)
в) 
-Вспомните формулу корней приведенного квадратного уравнения. ( )
)

Запишите формулу корней приведенного квадратного уравнения. ( )
)
Мотивация.
-Вы находитесь в конце изучения большой темы «Квадратное уравнение и его решения». Изучили много понятий, формул, теорем. На следующем уроке будет контрольная работа. Поэтому нужно подвести итог всему, что вы узнали о квадратных уравнениях.
Постановка учебной задачи урока.
- Цель сегодняшнего урока: провести систематизацию и обобщение изученного материала по теме: «Квадратное уравнение и его решение», вспомнить основные виды задач по данной теме и способы их решения.
Тема урока «Квадратное уравнение и его решение» (учитель записывает на доске, а ученики в тетрадях).
Содержательный этап.
Работа идет фронтально, письменно, ученики по очереди вызываются к доске.
№4. Не вычисляя корней  и
и  уравнения
уравнения  , найдите
, найдите
 .
.
-Ребята, чему, по теореме Виета, равна сумма корней? (сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком).
-А произведение корней чему равно? (произведение корней равно свободному члену).
Выполняются соответствующие записи в канве-таблице2.
Ответы:


По теореме Виета:

Первое уравнение системы возводим в квадрат:



Мы знаем, что 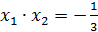 (второе уравнение системы), тогда
(второе уравнение системы), тогда





Ответ:  .
.
-Ребята, сформулируйте теорему, обратную теореме Виета. (. Если числа  таковы, что
таковы, что  , то
, то  и
и  - корни уравнения
- корни уравнения  )
)
Выполняются соответствующие записи в канве-таблице2.
№5. Составьте квадратное уравнение по его корням.
а) 5 и 2; б)  и
и 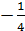
решение:
а)  (по теореме, обратной теореме Виета), тогда
(по теореме, обратной теореме Виета), тогда 
б)  (по теореме, обратной теореме Виета), тогда
(по теореме, обратной теореме Виета), тогда  .
.
-Ребята, давайте подумаем, как будет формулироваться теорема Виета, если уравнение не будет приведенным?
(сумма корней квадратного уравнения равна коэффициенту при  , взятому с противоположным знаком и деленному на коэффициент при
, взятому с противоположным знаком и деленному на коэффициент при  ; произведение корней этого уравнения равно свободному члену, деленному на коэффициент при
; произведение корней этого уравнения равно свободному члену, деленному на коэффициент при  :
:  ,
,  ).
).
-Эта теорема называется обобщенной теоремой Виета. Ребята, как тогда будет формулироваться теорема, обратная обобщенной теореме Виета?
(Если выполняются равенства  ,
,  , то числа
, то числа  и
и  являются корнями квадратного уравнения
являются корнями квадратного уравнения  ).
).
-Ребята, мы знаем ещё одну теорему, теорему о разложении квадратного трехчлена на множители. Сформулируете её. (Если  и
и  - корни квадратного уравнения
- корни квадратного уравнения  , то при всех
, то при всех  справедливо равенство
справедливо равенство  )
)
Выполняются соответствующие записи в канве-таблице2.
№6. Сократите дробь.
1) 









2) 


 ,
, 



 ,
, 


-Ребята, какое уравнение называется биквадратным? (уравнение
 , где
, где  ).
).
Выполняются соответствующие записи в канве-таблице1.
№7. Решите уравнение:
1)  2)
2) 
Решение.
1) 



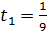 ,
, 




Ответ:  ,
,  ,
,  ,
, 
3) 






 – посторонний корень.
– посторонний корень.
Ответ: 
№8. Отношение гипотенузы прямоугольного треугольника к его катету равно 13:12, а другой катет равен 15 см. Найдите периметр треугольника.
Пусть гипотенуза равна  , тогда катет равен
, тогда катет равен  .
.
По теореме Пифагора 
-Ребята, дорешаете эту задачу дома.
Решение.



 - не удовлетворяет условию, так как гипотенуза треугольника не может равняться отрицательному числу.
- не удовлетворяет условию, так как гипотенуза треугольника не может равняться отрицательному числу.

Получаем, что гипотенуза равна  , а катет
, а катет  .
.
Тогда периметр треугольника равен  .
.
Ответ: 90 см.
№9. Решите систему уравнений:

-Ребята, как вы будите решать эту систему?
(методом подстановки: выразим  из второго уравнения и подставим в первое, найдем
из второго уравнения и подставим в первое, найдем  , подставим его во второе уравнение и найдем
, подставим его во второе уравнение и найдем  )
)
-Решите эту систему дома.
Решение.


 ,
,
 ,
,


Ответ:  ;
;  .
.