Б.ст.(коническая) Т.ст.(цилиндрическая)

Основные параметры привода

2.1.1 Параметры редуктора

Б.ст. (коничес- кая)	de 2	de 1	dm 2	dm 1	b	Re	Kbe	mte	mnm
	62,5	214,13	53,53		128,85	0,287	3,9063	2,7407
d1	z 1	z 2	u Б
14,036243 0
Т.ст. (цилинд- рическая)	aW	bW	mn	b	z 1	z 2	u Т	d 1
			11,777577 0			3,96	76,61
d 2	df 1
303,39	69,11

Действительное передаточное число редуктора

u _ред = u _Б u _Т = 4×3,96 = 15,84.

2.1.2 Общее передаточное число привода

u ₀ = i × u _ред = 1,62×15,84 = 25,66.

Отклонение D u ₀ от u ₀¢ = 25 (таблица 1.3) D u ₀ = 100 (25 – 25,66)/ 25 =

= – 2,64% < [±4%] – в пределах допуска.

Уточнение n_i и T_j по формулам (1.6) и (1.7):

Вал (рисунок 1.2)	I	II	III	IV	V
ni, мин-1		882,7	220,7	55,7	55,7
Tj, Н×м	40,8	63,1	241,8

Скорости v_{m 1} = 2,47 м/c; v ₁ = 0,89 м/с.

2.1.3 Диаметры валов редуктора, мм:

под зубчатыми колесами	d Б = 32	d П = 40	d Т = 56
под подшипниками качения	d БП = 35	d ПП = 35	d ТП = 55

Диаметр вала приводного барабана d = 55 мм.

 

Проверочный расчет зубчатых передач редуктора

Проверка выбора механических характеристик материала

Диаметры заготовок шестерен z ₁ [2, c.5]:

быстроходная (коническая) ступень	тихоходная (цилиндрическая) ступень
D ¢ = dae 1 + 6,	D ¢ = da 1 + 6
где [3, c.14] dae 1 = de 1 + 1,64 (1+ xn 1) mte cosd1 –	da 1 = 82,61 мм
внешний диаметр вершин зубьев;	D ¢ = 82,61 + 6 = 88,61 мм < [125 мм]
xn 1 = 2 (1 – 1/ u 2) (cos3b m / z 1)1/2 –
коэффициент высотной коррекции зубьев [3, c.3]: xn 1 = 2 (1 – 1/ 42) (cos3350 / 16) 1/2 = 0,348
dae 1 = 62,5 + 1,64 (1+ 0,348)×3,9063 х х cos 14,0362430 = 70,88 мм
D ¢ = 70,88 + 6 = 76,88 мм < [125 мм].
Толщины ободов заготовок колес [2, c.5]:
быстроходная ступень	тихоходная ступень
S ¢ = d = 2,5 mte +2 = 2,5×3,9063 + 2 = 11,8 мм S ¢ = с = 0,3 b = 0,3×37 = 11,1 мм   S ¢ = 11,8 мм < [80 мм]	S ¢ = d = 2,2 m + 0,05 b 2 = 2,2×3 + 0,05×60 = 9,6 мм S ¢ = с = 0,3 b 2 = 0,3×60 = 18 мм S ¢ = 18 мм < [80мм]

Механические характеристики материала обеих ступеней редуктора по размерам заготовок выбраны правильно.

Допускаемые напряжения

2.2.2.1 Допускаемые расчетные контактные напряжения (таблица 1.7) не изменились: – быстроходная ступень s _НР = 530 МПа;

– тихоходная ступень s _НР = 600 МПа.

2.2.2.2 Уточненные допускаемые напряжения на сопротивление усталос-ти при изгибе определяют раздельно для z ₁ и z ₂ по формуле [3, c.14]:

s _FР = s _{F lim b} Y_NY _d Y_RY_X / S_F, (2.1)

где _{__} s _{F lim b} » s _{F lim}⁰ = 550 МПа (с.15) – базовый предел выносливости на изгиб;

S_F = 1,7 [2, c.11] – коэффициент запаса прочности;

Y_N – коэффициент долговечности; так как N_FE > N_{F lim} = 4×10⁶. то Y_N = 1;

Y _d = 1,082 – 0,172 lg m [3, c.14] – опорный коэффициент:

– быстроходная ступень Y _d = 1,082 – 0,172 lg 3,9063 = 0,98;

– тихоходная ступень Y _d = 1,082 – 0,172 lg 3 » 1,0;

Y_R – коэффициент шероховатости переходной поверхности [3, c.14]: при зубофрезеровании и шлифовании Y_R = 1,0;

Y_X =1 (d < 400 мм) – коэффициент, учитывающий размеры зубчатых колес.

По формуле (2.1) будем иметь:

– Б.ст. s _{FР 1,2} = 550×1×0,98×1×1 / 1,7 = 317 МПа;

– Т.ст. s _{FР 1,2} = 550×1×1×1×1 / 1,7 = 324 МПа.

2.2.2.3 Допускаемые напряжения при действии максимальной нагрузки [3, c.15]: – z ₁: закалка ТВЧ; s _{НР max} = 44 HRC _Э = 44×47,5 = 2090 МПа;

– z ₂: улучшение s _{НР max} = 2,8 s_Т = 2,8×750 = 2100 МПа.

Предельные напряжения зубьев при изгибе [3, c.15]:

s _FSt = s _{F lim b} Y_{N max} K_St,

где при q_F = 6 _{_} Y_{N max} = 4; K_St = 1,3; s _FSt = 550×4×1,3 = 2860 МПа.

Допускаемые изгибные напряжения при действии максимальной нагрузки [3, c.15]: s _{FР max} = s _FSt Y_X / S_FSt,

где S_FSt – коэффициент запаса прочности: S_FSt = 1,75 Y_Z – при 99%-ной вероятности неразрушения зубьев;

Y_Z - коэффициент, учитывающий способ получения заготовки:

– z ₁: заготовка – прокат, Y_{Z 1} = 0,9;

– z ₂ – заготовка – поковка, Y_{Z 2} = 1,0.

Тогда S_{FSt 1} = 1,75×0,9 = 1,58; S_{FSt 2} = 1,75×1 = 1,75;

s _{FР max1} = 2860×1 / 1,58 = 1810 МПа; s _{FР max2} = 2860×1 / 1,75 = 1630 МПа.

2.2.3 Коэффициенты расчетной нагрузки K_AK_VK _b K _a

2.2.3.1 Коэффициенты K_V [3, c.6]:

K_V = 1 + w_Vb_W / (F_tK_A),

где w_V – удельная окружная динамическая сила, Н / мм, для передачи [3,c.7, 9]:

конической	цилиндрической
wV = d g 0 vm Ö dm 1(u +1) / u £ wV max;	wV = d g 0 v Ö aW / u £ wV max ,

где d – коэффициент, учитывающий влияние вида зубчатой передачи и моди-фикации профиля головки зубьев [3, c.7, 8];

g ₀ – коэффициент, учитывающий влияние разности шагов зацепления z ₁ и z ₂ [3, c.7].

Окружное усилие, Н:

Ft = 2000 T 1 / dm 1 ;

Ft = 2000 T 1 / d 1

Результаты расчета K_HV и K_FV приведены в таблице 2.1.

2.2.3.2 Коэффициенты K_{Н b} и K_{Н a} [3, c.7] не изменились (см. таблицу 1.9)

		KН b0	KН b	KН a0	KН a
	Б.ст.	2,72	1,65	1,0	1,0
	Т.ст.	1,24	1,1	1,6	1,26

_{_}Таблица 2.1 – Коэффициенты K_V

Ступень редуктора	П а р а м е т р ы
	Ft	d	g 0	wV	wV max	KV
быстроходная (коническая)	KHV		0,02	5,6	2,26		1,035
KFV	0,08	9,04	1,142
тихоходная (цилиндрическая)	KHV		0,02	0,69	1,007
KFV	0,06	2,07	1,02

Коэффициенты K_{F b}, K_{F a} при расчете на изгиб:

передача коническая [2, c.18]	передача цилиндрическая [2, c.17]
KF b¢ = 0,18 + 0,82 KН b0 = 0,18 + 0,82×2,72 = = 2,41; KF b = Ö KF b¢ = Ö 2,41 = 1,55 > 1,15.	KF b = 0,18 + 0,82 KН b0 = = 0,18 + 0,82×1,24 = 1, 2;
KF a = 1,0	KF a = KН a0 = 1,6 > 1,4.

2.2.3.3 Коэффициенты расчетной нагрузки для передачи:

конической	цилиндрической
KH = 1×1,035×1,65×1 = 1,71;	KH = 1×1,007×1,1×1,26 = 1,4;
KF = 1×1,142×1,55×1 = 1,78;	KF = 1×1,02×1,2×1,6 = 1,96.

 

2.2.4 Контактные напряжения s _Н и s _{Н max}

2.2.4.1 Коэффициенты Z в формуле [3, c.5]:

s _Н = Z_EZ_HZ _e Ö F_tK_H (u +1) / (b_Wd ₁ u) £ s _НР (2.2) _{_}

а) Коэффициент механических свойств материалов z ₁ и z ₂ (сталь)

Z_E = 190 МПа^1/2;

б) Коэффициент формы сопряженных поверхностей зубьев

Z_H = (2 cosb _b / tga _tW)^1/2 / cosa _t,

где a _t = arctg (tg20⁰ / cosb) = arctg (tg20⁰ / cos 11,777577⁰) = 20,395⁰ – дели-тельный угол профиля в торцовом сечении; при х ₁ + х ₂ = 0 угол зацепления a _tW = a _t; b _b = arcsin (sinbcos20⁰) = arcsin (sin11,777577⁰cos20⁰) = 11,058⁰-

основной угол наклона зубьев;

Z_H = (2 cos11,058⁰ / tg20,395⁰)^1/2 / cos20,395⁰ = 2,45;

в) Коэффициент суммарной длины контактных линий

Z _e = (1 / e_a)^{1/ 2},

где e_a » [1,88 – 3,2 (1/ z ₁ + 1/ z ₂)]cosb - коэффициент торцового перекрытия при х ₁ + х ₂ = 0;

e_a = [1,88 – 3,2 (1/ 25 + 1/ 99)] cos11,777577⁰ = 1,68;

Z _e = (1 / 1,68)^{1/ 2} = 0,77.

Произведение коэффициентов Z = Z_EZ_HZ _e = 190×2,45×0,77 = 358,4 2.2.4.2 Контактные напряжения цилиндрической передачи

по формуле (2.2)

s _Н = 358,4 Ö 6310×1,4 (3,96 + 1) / (60×76,61×3,96) = 556 МПа,

что меньше s _НР = 600 МПа – условие прочности выполняется.

2.2.4.3 Контактные напряжения конической передачи [3,c.9]:

s _H = 3×10⁴ Ö T ₁ K_H / [u _Hd_{e 1}³ uK_be (1 – K_be)] £ s _HP (2.3)

s _H = 3×10⁴ Ö 63,1×1,71 / [1,65×62,5³×4×0,287 (1 – 0,287)] = 543 MПа –

превышение над s _HP = 530 МПа на Ds = 100 (543 – 530) / 530 = 2,45% < [5%],

что допустимо.

2.2.4.4 Максимальные напряжения при кратковременной перегрузке [3,c.8]: s _{H max} = s _H (T _max/ T) ^{1/ 2} £ s _{HP max},

где T _max/ T =2,5 – по характеристике двигателя (таблица 1.2).

Для конической передачи

s _{H max} = 543×(2,5) ^{1 / 2} = 859 МПа < 2090 МПа;

для цилиндрической передачи

s _{H max} = 556×(2,5) ^{1 / 2} = 879 МПа < 2090 МПа.

2.2.5 Напряжения изгиба s _F и s _{F max}

2.2.5.1 Коническая передача [3,с.9]:

s _{F 1} = 2700 T ₁ K_FY_{FS 1} / (u _F bd_{e 1} m_te) £ s _{FP 1}; (2.4)

s _{F 2} = s _{F 1} Y_{FS 2}/ Y_{FS 1} £ s _{FP 2}, (2.5)

где Y_FS = 3,47 + 13,2 / z_v – 27,9 x / z_v + 0,092 x ² – (2.6)

коэффициент формы зуба [3,c.8];

z_v = z / (cosd cos³b _m) – биэквивалентное число зубьев [3,c.10]:

z_{v 1} = 30, z_{v 2} = 480;

x ₁ = x_{n 1} = 0,348 (c.22), x ₂ = – x_{n 2} = – 0,348; Y_{FS 1}= 3,6; Y_{FS 2} = 3,51;

u _F = 0,85 + 0,043×4 = 1,022 – коэффициент влияния вида конической передачи [3,c.10];

s _{F 1} = 2700×63,1×1,78×3,6 / (1,022×37×62,5×3,9063) = 118 МПа;

s _{F 2} = 118×3,51 / 3,6 = 115 МПа, что меньше s _{F P} = 317 МПа – условие

изгибной выносливости зубьев выполняется.

2.2.5.2 Цилиндрическая передача [3, c.7]:

s _F = F_tK_FY_FSY _b Y _e / (b_wm_n) £ s _FP, (2.7) где Y_FS – по формуле (2.6) в зависимости от эквивалентного числа зубьев z_v = z / cos³b (z_{v 1} = 27, z_{v 2} = 106) при x = 0; Y_{FS 1} = 3,96; Y_{FS 2} = 3,59;

Y _b=1– e_bb⁰ / 120 ³ 0,7 – коэффициент наклона зубьев [3,c.8]

где e_b = b_w sinb / p m = 1,36 – коэффициент осевого перекрытия;

Y _b = 1 – 1,36×11,777577 / 120 = 0,87 > 0,7;

Y _e = 1/e_a = 1 / 1,68 = 0,6 – коэффициент перекрытия зубьев.

Критерий расчета на изгиб: s _{FP 1} / Y_{FS 1}= 324 / 3,96 = 81,82;

s _{FP 2} / Y_FS2 = 324 / 3,59 = 90,25 – расчет следует вести по зубу шестерни Z _1.

По формуле (2.6) s _{F 1}= 6310×1,96×3,96×0,87×0,6 / (60×3) = 142 МПа, что

меньше s _FP =324 МПа – условие изгибной выносливости зубьев выполняется.

2.2.5.3 Максимальные изгибные напряжения при кратковременной перегрузке [3,c. 8]: s _{F max} = s _F (T_max/ T) £ s _{FP max},

где для конической передачи s _{F max1}= 118×2,5 = 295 МПа < 1810 МПа;

для цилиндрической передачи s _{F max1}= 142×2,5 = 355МПа < 1810 МПа.

Условие прочности выполняется.

2.2.6 Основные размеры конических зубчатых колес с осевой формой зубьев II [8, c.195], [4, c.14] представлены в таблице 2.2

Таблица 2.2 – Основные размеры конических зубчатых колес

Параметр конического зубчатого колеса	Результат
наименование	формула
1 Высота головки зуба в среднем сечении, мм, (xn 1 = 0,348)	ha 1 = (1+ xn 1) mnm ha 2 = 2 mnm – ha 1	3,6945 1,7869
2 Нормальная толщина зуба в среднем сечении,мм (x t1 = 0,125)	Snm 1 = (0,5p + 2 xn 1tga n + x t1) mnm Snm 2 p mnm – Snm 1	5,342 3,2682
3 Среднее конусное расстояние, мм	Rm = Re – 0,5 b	110,35
4 Суммарное число зубьев	zc = (z12 + z22)1/2	65,97
5 Промежуточные расчетные величины	C 1 = 10800tgb m / tg a n	20775,4
	d ин = (1,5...2,3) Rm = 1,9 Rm	209,67
	C2 = 2 C 1sinb m / d ин	113,67
	a' = (C 1 – C2 Rm) / zc	124,78
	a (округление)
6 Сумма углов ножек z 1 и z 2, мин	q f S = a / sin b m	209,21
7 Углы ножек зубьев	q f 1 = q f S Snm 2 / p mnm   q f 2 = q f S – q f 1	79,41 ' (1,32350) 129,8 ' (2,16330)
8 Увеличение высоты головки при переходе на внешний торец, мм	D ha 1 = 0,5 b tgq f 2 D ha 2 = 0,5 b tgq f 1	0,6988 0,4274
9 Внешняя высота головки зуба,мм	hae 1 = ha 1 + D ha 1 hae 2 = ha 2 + D ha 2	4,3933 2,2143
10 Внешняя высота зуба, мм	c = 0,2 mte	0,7813
	k = c + D ha 1 + D ha 2	1,9075

 

Окончание табл. 2.2

Параметр конического зубчатого колеса	Результат
наименование	формула
	he 1 = 2 ha 1 + k he 2 = 2 ha 2 + k	9,2965 5,4813
11 Внешний диаметр вершин зубьев, мм	dae 1 = de 1 +2 hae 1cosd1 dae 2 = de 2 +2 hae 2cosd2	71,02 251,07
12 Расстояние от вершины до плоскости внешней окружности, мм	A 1 = 0,5 dae 2 – hae 1sind1 A 2 = 0,5 dae 1 – hae 2sind2	124,47 33,36

2.2.7 Проверка выполнения конструктивных ограничений передач [3,c.18]

2.2.7.1 По условию прочности и жесткости валов [3,c.18, 19]:

Б.ст.(коническая) Т.ст.(цилиндрическая)

d_{m 1} ³ 1,35 d _Б d_{f 1} ³ 1,25 d _П

53,53 ³ 1,35×32 = 43,2 мм 69,11 ³ 1,25× 40 = 50 мм

Условия выполняются.

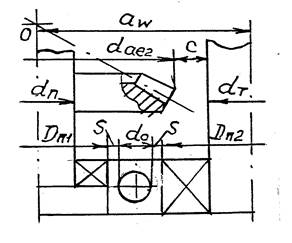
2.2.7.2 По условию размещения подшипников и стяжных болтов в пределах a_w [3,c.19] в соответствии с рисунком 2.1. Диаметр болтов крепления

крышки и корпуса d' = 1,25 T T1/3 ³ 10 мм; d' = 1,25×9281/3= 12,2 мм. Принимаем d = 12 мм. Диаметр отверстия в крышке под болт [3,c.19]: d 0=14 мм. Предварительно принимая на валах радиально – упорные подшипники легкой узкой серии по ГОСТ 27365–87, будем иметь: вал d, мм; типоразмер ПК D П, мм Промежуточный 35 7207А 72 Тихоходный 55 7211А 100, где D П – наружный диаметр подшипника Условие компоновки [3,c.19, (7.9)]: S = = 0,5(aw – d 0) – 0,25(D П1+ D П2) ³ 3...5 мм;

Рисунок 2.1

Рисунок 2.1

Диаметр болтов крепления крышки и корпуса d' = 1,25 T T1/3 ³ 10 мм; d' = 1,25×9281/3= 12,2 мм.Принимаем d = 12 мм.Диаметр отверстия в крышке под болт [3,c.19]: d 0=14 мм.Предвари- тельно принимая на валах радиально – упорные подшипники легкой узкой серии по ГОСТ 27365–87, будем иметь: Вал d, мм типоразмер ПК D П, мм промежуточ. 35 7207А 72 тихоходный 55 7211А 100 где D П –наружный диаметр подшинника

S = 0,5(190 – 14) – 0,25(72 + 100) = 45 >> 3...5 мм – условие компоновки в пределах a_w выполняется.

2.2.7.3 По условию обеспечения зазора С [3,c.19] в соответствии с рисун-ком 2.1: C = a_w – 0,5(d_{ae 2} + d _Т) ³ 3 мм; C = 190 – 0,5(251,07 + 56) = 36,47 >>

3 мм – условие непересечения коническим колесом тихоходного вала выполняется.