Лабораторная работа № 3
Цель работы: разложение несинусоидальной кривой графоаналитическим методом в ряд Фурье и определение коэффициентов, характеризующих несинусоидальную кривую. Определение влияния характера цепи (R; RL; RC) на форму кривой несинусоидального тока при подключении ее к источнику несинусоидального напряжения.
Любая несинусоидальная периодическая функция, может быть разложена в тригонометрический ряд Фурье: 
. (1)
Ряд Фурье может быть также записан в виде суммы постоянной составляющей и синусоид с начальными фазами, не равными нулю: 
. (2)
где n = 1,2,3 и т. д. – порядок гармоничных составляющих; 
; 
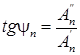. (3)
При определении начальной фазы, т.е. угла ψ n необходимо по знакам коэффициентов 
и 
определить, в какой четверти находится этот угол:
если >0, то 
; (4)
если <0, то 
. (5)
Коэффициенты ряда определяются по формуле Фурье:
постоянная составляющая: 
; (6)
амплитуды синусных составляющих: 
; (7)
амплитуды косинусных составляющих: 
. (8)
Графоаналитический метод определения гармоник ряда Фурье основан на замене определенного интеграла суммой конечного числа слагаемых. С этой целью период функции f (w t) равный 2p разбивают на m равных частей: 
, (9)
находят соответствующие ординаты кривой f 1 ( ω t); f 2 ( ω t); f 3 ( ω t) и заменяют интегралы частичными суммами:
; (10)
; (11)
, 
(12)
где p – текущий индекс, он изменяется от 1 до m; fP( ω t) – значение функции при ω t = p Dω t.
Порядок нахождения коэффициентов ряда Фурье и определения параметров несинусоидального сигнала графоаналитическим методом:
1. Полный период заданной периодической кривой f( ω t) делят на равное число частей, положим на m = 24 и находят соответствующие ординаты кривой f( ω t): f 1, f 2, f 3 …fm.
2. Пользуясь табл.1, в соответствии с формулами (11) и (12) определяют амплитуды гармоник.
Если кривая симметрична относительно оси абсцисс, то расчет производится за половину периода. При этом в формулах (11) и (12) перед знаком суммы будет стоять множитель не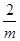 
, а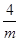 
.
Для кривых, симметричных относительно оси абсцисс, достаточно найти координаты за полпериода, т.е. для 
= 12 значений, так как координаты во второй части полупериода будут иметь такую же величину, как и в первой половине, но только с противоположным знаком.
В результате формулы (11) и (12) принимают вид:
; 
.
3. По формуле (3) определяем амплитуду каждой рассчитываемой гармонической составляющей напряжения.
4. По формулам (3-6) рассчитываем начальную фазу каждой гармонической составляющей напряжения.
5. Записываем ряд Фурье с использованием формулы (2).
6. Действующие значения несинусоидального тока и напряжения рассчитывают по формулам:
(13)
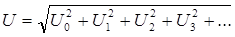(14)
где I 0 и U 0 – постоянные составляющие; I 1, I 2, I 3…, U 1, U 2, U 3… – действующие значения токов и напряжений гармоник.
7. Коэффициентами, характеризующими периодические несинусоидальные функции, являются:
коэффициент амплитуды: 
или 
(15)
коэффициент формы: 
или 
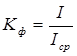(16)
коэффициент искажения: 
или 
(17)
Порядок выполнения работы
1. В работе исследуется графоаналитический метод разложения несинусоидальной функции в ряд Фурье (лаб. раб. №13). Параметры схемы задает компьютер по шифру студента. Источник питающего напряжения имеет несинусоидальную форму выходного напряжения.
2. Для разложения несинусоидальной кривой в ряд Фурье необходимо определить ординаты заданной кривой через каждые 15 эл. градусов. Для этого с помощью указателя мыши измерить значения несинусоидального напряжения в дискретных точках, находящихся на кривой напряжения источника питания через каждые 15 эл. градусов. Данные записать в табл.1.
3. Пользуясь табл.1 и формулами (11) и (12) разложить заданную несинусоидальную кривую на гармонические составляющие до 5-ой гармоники включительно. Результаты записать в табл. 2.
Выбрать опцию «2 шаг». На экране появятся точки, принадлежащие несинусоидальной кривой. Ввести данные из табл.2 в таблицу, находящуюся в правой части экрана. После этого нажать кнопку «Обновить». На экране появятся отдельные гармоники и результирующая кривая. Если разложение выполнено правильно, то результирующая кривая пройдет через заданные точки. Отклонение от заданных точек свидетельствует об ошибках в разложении несинусоидальной кривой в ряд Фурье.
Таблица 2
| A 1 (U 1 m ) | A 3 (U 3 m ) | A 5 (U 5 m ) | Ψ1 | Ψ3 | Ψ5 | Ки | |||
| В | % | В | % | В | % | эл. град. | эл. град. | эл. град. | – |
| 100 % |
4. Выбрать опцию «шаг 3». Наблюдать форму кривой тока при подключении к источнику несинусоидального напряжения цепи с:
а) активным сопротивлением (включен ключ В1);
б) активно-индуктивным сопротивлением (включен ключ В2);
в) активно-емкостным сопротивлением (включен ключ В3).
5. Сделать вывод о влиянии индуктивности и емкости на форму кривой тока.
6. Записать ряд Фурье для разложенной функции напряжения. Построить гармоники тока и результирующую несинусоидальную кривую в одних осях координат за время одного периода, пользуясь интегрированной программой MATHCAD.
7. Сделать заключение о проделанной работе.
Таблица 1
| Текущий индекс p | fp (w t) | n =1 | n =3 | n =5 | ||||||||||||
| p (2pm) | sin p (2p/ m) | сos p (2p/ m) | fp (w t) sin p(2p/ m) | fp (w t) cos p (2p/ m) | 3 p (2p/ m) | sin 3 p (2p/ m) | cos 3 p (2p/ m) | fp (w t) sin 3 p (2p/ m) | fp (w t) cos 3 p (2p/ m) | 5p (2p/ m) | sin 5 p (2p/ m) | cos 5 p (2p/ m) | fp (w t) sin 5 p (2p/ m) | fp (w t) cos 5 p (2p/ m) | ||
| +0,259 | +0,966 | +0,707 | +0,707 | +0,966 | +0,259 | |||||||||||
| +0,500 | +0,866 | +1,0 | +0,5 | -0,866 | ||||||||||||
| +0,707 | +0,707 | +0,707 | -0,707 | -0,707 | -0,707 | |||||||||||
| +0,866 | +0,500 | -1,0 | -0,866 | +0,5 | ||||||||||||
| +0,966 | +0,259 | -0,707 | -0,707 | +0,259 | +0,966 | |||||||||||
| +1,0 | -1,0 | +1,0 | ||||||||||||||
| +0,966 | -0,259 | -0,707 | +0,707 | +0,259 | -0,966 | |||||||||||
| +0,866 | -0,500 | +1,0 | -0,866 | -0,5 | ||||||||||||
| +0,707 | -0,707 | +0,707 | +0,707 | -0,707 | +0,707 | |||||||||||
| +0,500 | -0,866 | +1,0 | +0,5 | +0,866 | ||||||||||||
| +0,259 | -0,966 | +0,707 | -0,707 | +0,966 | -0,259 | |||||||||||
| 0,0 | -1,0 | -1 | -1,0 | |||||||||||||
| S | S | S | ||||||||||||||
| 
| 
| 
| 
| 
|
| 
| 
|
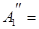
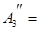
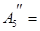
Примечание: расчет вести с точностью до трех знаков после запятой.
Студент ____________________ Дата ________
Вопросы допуска к лабораторной работе №3:
1 Запишите разложение периодических несинусоидальных кривых в гармонический ряд Фурье (в полной и сокращенной формах записи).
2 Как определяются коэффициенты ряда Фурье в интегральной форме?
3 Как связаны между собой коэффициенты полной и сокращенной формы записи ряда Фурье?
4 Как определяется действующее значение периодической несинусоидальной переменной?
5 Как определяется мощность в цепях периодического несинусоидального тока?
6 Сформулируйте методику расчета гармонических составляющих ряда Фурье графоаналитическим методом.
 | |||
 |