Иное рассуждение в пункте б).

Заметив, что можно было бы заключить, что сечением является ромб, и найти его площадь как половину произведения диагоналей.

 

Теоремы, используемые при построении сечений

 

Алгоритм построения сечений

16. Дана правильная четырёхугольная пирамида MABCD, все рёбра которой равны 12. Точка N — середина бокового ребра MA, точка K делит боковое ребро MB в отношении 2: 1, считая от вершины M.

а) Докажите, что сечение пирамиды плоскостью, проходящей через точки N и K параллельно прямой AD, является равнобедренной трапецией.

б) Найдите площадь этого сечения.

Решение.

а) Через точки N и K проведём прямые, параллельные ребру AD. Эти прямые пересекают рёбра MD и MC в точках P и L соответственно. Четырёхугольник KLPN — сечение пирамиды указанной плоскостью. Стороны NP и KL параллельны и не равны. Следовательно, KLPN — трапеция. В треугольниках NMK и PML углы при вершине M равны, ML = MK, MN = MP. Следовательно, треугольники равны, и поэтому NK = PL. Таким образом, трапеция KLPN равнобедренная.

б) Пусть NH — высота трапеции KLPN. Имеем

Найдём NK из треугольника NMK. Имеем NM = NP = 6, MK = KL = 8. По теореме косинусов,

Поскольку трапеция равнобедренная,

По теореме Пифагора из треугольника KHN получаем:

Следовательно, площадь трапеции равна

 

Ответ: б)

17. В основании правильной пирамиды PABCD лежит квадрат ABCD со стороной 6. Сечение пирамиды проходит через вершину В и середину ребра PD перпендикулярно этому ребру.

а) Докажите, что угол наклона бокового ребра пирамиды к её основанию равен 60°.

б) Найдите площадь сечения пирамиды.

Решение.

а) Углом между прямой и плоскостью называется угол между прямой и ее проекцией на эту плоскость. Поскольку заданная четырёхугольная пирамида правильная, ее вершина проектируется в точку пересечения диагоналей лежащего в основании квадрата. Поэтому проекцией прямой PB на плоскость основания является прямая BD. Найдем угол PBD.

Пусть M — середина PD. Так как прямая BM лежит в плоскости сечения, перпендикулярного PD, отрезки BM и PD перпендикулярны, то есть в треугольнике BPD медиана BM является высотой. Значит, BP = BD, но, так как PB = PD, треугольник BPD равносторонний, а поэтому что и требовалось доказать.

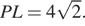б) Из доказанного следует, что и как высота равностороннего треугольника BPD. Применяя теорему косинусов в треугольнике APD, получаем откуда Пусть BKML — указанное сечение (точка K лежит на ребре PA, а точка L — на ребре PC). Так как отрезки KM и PD перпендикулярны, Аналогично находим Значит, а потому треугольник PKL подобен треугольнику PAC. Поэтому Кроме того, прямые KL и AC параллельны, а прямые AC и BM перпендикулярны, так как AC перпендикулярна плоскости BPD, а BM лежит в этой плоскости. Значит, прямые KL и BM перпендикулярны. Поэтому искомая площадь равна

 

 

Ответ:

18. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ: QB = 1: 2. Точка P — середина ребра AS.

а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.

б) Найдите площадь сечения DPQ, если площадь сечения DSB равна 6.

Решение.

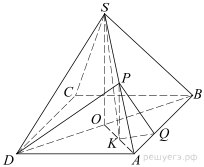
а) Пусть O — центр основания пирамиды, точка M — середина ребра AD, отрезки AO и DQ пересекаются в точке K, а отрезки MO и DQ пересекаются в точке N. Тогда MO — средняя линия в треугольнике ADB, а NO — средняя линия в треугольнике QDB. Значит,

Таким образом, треугольники AKQ и OKN равны. Следовательно, точка K — середина отрезка AO. Значит, прямая PK содержит среднюю линию треугольника ASO, поэтому она перпендикулярна плоскости основания пирамиды SABCD. Плоскость DPQ содержит прямую PK, поэтому она тоже перпендикулярна плоскости основания.

б) Пусть сторона основания пирамиды равна а высота пирамиды равна h. Тогда площадь сечения DSB равна

откуда Площадь сечения DPQ равна

 

Ответ: б)

19. На ребре AB правильной четырёхугольной пирамиды SABCD с основанием ABCD отмечена точка Q, причём AQ: QB = 1: 2. Точка P — середина ребра AS.

а) Докажите, что плоскость DPQ перпендикулярна плоскости основания пирамиды.

б) Найдите площадь сечения DPQ, если площадь сечения DSB равна

Решение.

а) Пусть O — центр основания пирамиды (рис.1), точка M — середина ребра AD, отрезки AO и DQ пересекаются в точке K, а отрезки MO и DQ пересекаются в точке N (рис.2). Тогда MO — средняя линия в треугольнике ADB, а NO — средняя линия в треугольнике QDB. Значит,

Таким образом, треугольники AKQ и OKN равны. Следовательно, точка K — середина отрезка AO. Значит, прямая PK содержит среднюю линию треугольника ASO, поэтому она перпендикулярна плоскости основания пирамиды SABCD. Плоскость DPQ содержит прямую PK, поэтому она тоже перпендикулярна плоскости основания.

б) Пусть сторона основания пирамиды равна а высота пирамиды равна h. Тогда площадь сечения DSB равна

откуда Площадь сечения DPQ равна

 

Ответ: б)

20. В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD со стороной 6. Противоположные боковые рёбра пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость α, параллельная ребру MC.

а) Докажите, что сечение плоскостью α пирамиды MABC является параллелограммом.

б) Найдите площадь сечения пирамиды MABC плоскостью α.

Решение.

а) Пусть точка Q — середина ребра MA, а точка K — середина ребра MB. Плоскость пересекает плоскость BMC по отрезку KL, параллельному ребру MC. Следовательно, плоскость пересекает плоскость AMC по прямой, параллельной ребру MC. На этой прямой лежит средняя линия треугольника AMC, поэтому плоскость проходит через точку O — середину отрезка AC. Таким образом, сечение — четырёхугольник QKLO, в котором стороны KL и QO параллельны отрезку MC и равны его половине. Значит, QKLO —параллелограмм.

б) Отметим точку F — середину отрезка QK и рассмотрим плоскость MOF. Прямая QK перпендикулярна прямым FM и MO, следовательно, она перпендикулярна плоскости MFO, поэтому она перпендикулярна отрезку OF. Таким образом, отрезок OF служит высотой параллелограмма QKLO. Сечение пирамиды MABCD плоскостью MOF — равнобедренный

треугольник NMG. Отрезок OF является медианой прямоугольного треугольника MOG, проведённой к его гипотенузе, поэтому

По условию треугольник AMC прямоугольный и равнобедренный, поэтому

 

 

и то же верно для других боковых рёбер. Следовательно, все боковые грани пирамиды — равносторонние треугольники. Тогда и

Площадь параллелограмма QKLO равна

 

Ответ:

21. В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD со стороной 4. Противоположные боковые рёбра пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость α, параллельная ребру MС.

а) Докажите, что сечение плоскостью α пирамиды MABC является параллелограммом.

б) Найдите площадь сечения пирамиды MABC плоскостью α.

Решение.

а) Пусть точка Q — середина ребра MA, а точка K — середина ребра MB. Плоскость пересекает плоскость BMC по отрезку KL, параллельному ребру MC. Следовательно, плоскость пересекает плоскость AMC по прямой, параллельной ребру MC. На этой прямой лежит средняя линия треугольника AMC, поэтому плоскость проходит через точку O — середину отрезка AC. Таким образом, сечение — четырёхугольник QKLO, в котором стороны KL и QO параллельны отрезку MC и равны его половине. Значит, QKLO —параллелограмм.

б) Отметим точку F — середину отрезка QK и рассмотрим плоскость MOF. Прямая QK перпендикулярна прямым FM и MO, следовательно, она перпендикулярна плоскости MFO, поэтому она перпендикулярна отрезку OF. Таким образом, отрезок OF служит высотой параллелограмма QKLO. Сечение пирамиды MABCD плоскостью MOF — равнобедренный

треугольник NMG. Отрезок OF является медианой прямоугольного треугольника MOG, проведённой к его гипотенузе, поэтому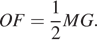

По условию треугольник AMC прямоугольный и равнобедренный, поэтому

 

 

и то же верно для других боковых рёбер. Следовательно, все боковые грани пирамиды — равносторонние треугольники. Тогда 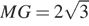и

Площадь параллелограмма QKLO равна

 

Ответ:

22. В правильной треугольной пирамиде MABC боковые рёбра равны 10, а сторона основания равна 12. Точки G и F делят стороны основания AB и AC соответственно так, что AG: GB = AF: FC = 1: 5.

а) Докажите, что сечение пирамиды плоскостью MGF является равнобедренным треугольником.

б) Найдите площадь сечения пирамиды плоскостью MGF.

Решение.

а) Из условия следует, что Треугольники AMG и AMF равны по двум сторонам и углу между ними. Поэтому

б) Проведём высоту MH боковой грани AMB. Из прямоугольного треугольника AHM находим

В прямоугольном треугольнике MHG катет HG равен 4. Поэтому

Треугольник AGF равносторонний, поэтому В равнобедренном треугольнике GMF проведём высоту MK. Она делит отрезок GF пополам. Из прямоугольного треугольника MKG получаем

Следовательно, площадь треугольника GMF равна

 

Ответ:

23. В основании правильной четырёхугольной пирамиды MABCD лежит квадрат ABCD. Противоположные боковые грани пирамиды попарно перпендикулярны. Через середины рёбер MA и MB проведена плоскость α, параллельная ребру MC.

а) Докажите, что плоскость α параллельна ребру MD.

б) Найдите угол между плоскостью α и прямой AC.

Решение.

а) Пусть точка Q — середина ребра MA, а точка K — середина ребра MB. Плоскость пересекает грань BMC по отрезку KL (точка L лежит на ребре BC), параллельному ребру MC. Ребро CD параллельно ребру AB, а ребро AB параллельно отрезку QK. Следовательно, плоскость параллельна плоскости грани CMD. Поэтому прямая MD параллельна плоскости .

б) Пусть длина стороны основания равна a. Вместо плоскости рассмотрим параллельную ей плоскость CMD. Проведём к ней перпендикуляр OH из центра основания — точки O. Рассмотрим сечение пирамиды плоскостью MOH. Это сечение — прямоугольный равнобедренный треугольник NMG, поскольку по условию грани CMD и AMB перпендикулярны. Отрезок OH параллелен катету MN этого треугольника и равен его половине:

 

Искомый угол равен углу HCO. В прямоугольном треугольнике OHC имеем:

 

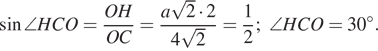
Ответ: б) 30°.

24. Через середину бокового ребра правильной треугольной пирамиды проведена плоскость α, перпендикулярная этому ребру. Известно, что она пересекает остальные боковые рёбра и разбивает пирамиду на два многогранника, объёмы которых относятся как 1 к 3.

а) Докажите, что плоский угол при вершине пирамиды равен 45°.

б) Найдите площадь сечения пирамиды плоскостью α, если боковое ребро пирамиды равно 4.

Решение.

а) Пусть P — вершина, ABC — основание пирамиды, M — середина ребра PA = 2 a. Пусть секущая плоскость пересекает рёбра BP и CP в точках E и F соответственно. Прямоугольные треугольники MPE и MPF равны по катету и острому углу; обозначим их равные гипотенузы PE = PF = x. Объём тетраэдра PMEF составляет

объёма пирамиды, что по условию равно объёма пирамиды. Отсюда и косинус плоского угла MPE при вершине равен поэтому

б) Поскольку все плоские углы при вершине пирамиды равны 45°, получаем, что ME = MF = 2. Из треугольника PEF по теореме косинусов

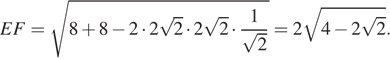
Высота MH равнобедренного треугольника MEF равна

Искомая площадь сечения равна

 

Ответ:

25. В основании пирамиды DABC лежит прямоугольный треугольник ABC с катетами AC = 15 и BC = 9. Точка M — середина ребра AD. На ребре BC выбрана точка E так, что CE = 3, а на ребре AC выбрана точка F так, что CF = 5. Плоскость MEF пересекает ребро BD в точке N. Расстояние от точки M до прямой EF равно

а) Докажите, что N — середина ребра BD.

б) Найдите площадь сечения пирамиды плоскостью MNF.

Решение.

а) Так как треугольники FEC и ABC имеют общий угол и то эти треугольники подобны. Значит, откуда Тогда и плоскость MEF пересекает плоскость ABD по прямой, параллельной прямой EF, а, следовательно, параллельной AB. Таким образом, отрезок MN — средняя линия треугольника ABD и точка N — середина ребра BD.

б) Сечение пирамиды плоскостью MNE — трапеция, высота h которой равна расстоянию от точки M до прямой EF, то есть Далее имеем:

Окончательно получаем:

Ответ: б)

26. В правильном тетраэдре ABCD точки K и M — середины рёбер AB и CD соответственно. Плоскость α содержит прямую KM и параллельна прямой AD.

а) Докажите, что сечение тетраэдра плоскостью α — квадрат.

б) Найдите площадь сечения тетраэдра ABCD плоскостью α, если

Решение.

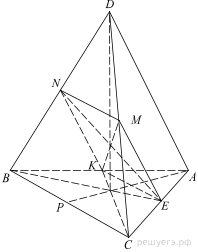
а) Пусть точки P, E, N — середины рёбер BC, AC и BD соответственно. ME — средняя линия следовательно, Аналогично Следовательно, 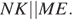Значит, точки N, K, M, E лежат в одной плоскости, причём эта плоскость параллельна прямой AD. Значит, это и есть плоскость

Поскольку тетраэдр правильный, то (как средние линии равных правильных треугольников). Значит, KNME — ромб.

Далее, Следовательно, (соответственные медианы этих треугольников). Поскольку ромб KNME является также прямоугольником. Следовательно, KNME — квадрат.

б) Площадь квадрата KNME находится по формуле 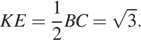Следовательно,

 

Ответ: б)

27. В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 5. На рёбрах AB и SC отмечены точки K и M соответственно, причём AK: KB = SM: MC = 5: 1. Плоскость α содержит прямую KM и параллельна SA.

а) Докажите, что сечение пирамиды SABC плоскостью α — прямоугольник.

б) Найдите объём пирамиды, вершиной которой является точка A, а основанием — сечение пирамиды SABC плоскостью α.

Решение.

а) Пусть точка H — середина ребра BC, а плоскость α пересекает ребра SB и АС в точках L и N соответственно. Тогда медианы АН и SH треугольников ABC и SBC соответственно являются их высотами, а значит, плоскость ASH перпендикулярна прямой BC. Следовательно, прямая SA перпендикулярна прямой BC.

Поскольку прямая SA параллельна плоскости α, прямые KL и MN параллельны прямой SA, а значит,

Следовательно, прямые LM и KN параллельны прямой BC.

Таким образом, KLMN является параллелограммом, пары противоположных сторон которого параллельны перпендикулярным прямым SA и BC соответственно, то есть KLMN — прямоугольник.

б) Прямая BC, параллельная прямой KN, перпендикулярна плоскости ASH, значит, плоскости ASH и α перпендикулярны.

Пусть плоскость ASH пересекает прямые KN и LM в точках E и F соответственно. Тогда высота пирамиды AKLMN равна расстоянию h между прямыми SA и EF.

Высота SO пирамиды SABC лежит в плоскости ASH, откуда

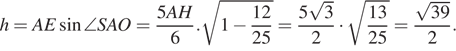
Объём пирамиды AKLMN равен

 

Ответ: б)