Площадь сечения состоит является суммой площади квадрата со стороной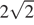 
и двух площадей равных равнобедренных треугольников с основанием 
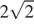и боковыми сторонами 
Площадь квадрата равна 8, площади треугольников находим как половину произведения высоты на основание 
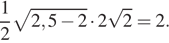Поэтому искомая площадь сечения равна 10.
11. В правильной четырехугольной призме ABCDA 1 B 1 C 1 D 1 точка K делит боковое ребро AA 1 в отношении AK: KA 1 = 1: 2. Через точки B и K проведена плоскость α, параллельная прямой AC и пересекающая ребро DD 1 в точке M.
а) Докажите, что плоскость α делит ребро DD 1 в отношении DM: MD 1 = 2: 1.
б) Найдите площадь сечения, если известно, что AB = 4, AA 1 = 6.
Решение.
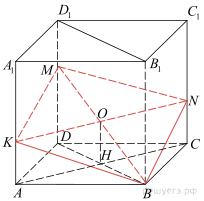Пусть четырёхугольник KBNM — сечение данной призмы плоскостью α (см. рисунок). Прямая AC параллельна плоскости α, а плоскость ACK пересекает плоскость α по прямой KN, следовательно, KN || AC и, значит, AKNC — прямоугольник. Прямые BD и AC являются соответственно проекциями прямых BM и KN на плоскость ABC, значит, точка пересечения прямых BD и AC (точка H) является проекцией точки пересечения прямых BM и KN (точки O) на эту плоскость. Таким образом, 
C другой стороны, отрезок OH — средняя линия треугольника BDM и, следовательно,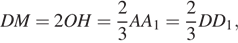 
откуда и следует доказываемое утверждение.
б) Так как AC ⊥ BD и AC ⊥ BB 1, то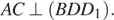 
Но KN || AC, значит, и 
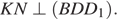Следовательно, KN ⊥ BM, поскольку 
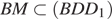и площадь сечения S равна 
Имеем:
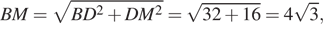
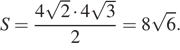
Ответ: б) 
12. В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известны длины рёбер: AB = 4, BC = 3, AA 1 = 2. Точки P и Q — середины рёбер A 1 B 1 и CC 1 соответственно. Плоскость APQ пересекает ребро B 1 C 1 в точке U.
а) Докажите, что B 1 U: UC 1 = 2: 1.
б) Найдите площадь сечения параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью APQ.
Решение.
а) Пусть прямые AP и BB 1 пересекаются в точке X (см. рисунок). Тогда точка U — точка пересечения прямых XQ и B 1 C 1.
|
|
Треугольники AXB и PXB 1 подобны, откуда
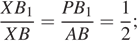
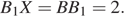
Треугольники B 1 XU и C 1 QU подобны, откуда
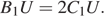
Значит.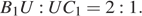 
б) Пусть Y — точка пересечения прямых QX и BC, а V — точка пересечения прямых CD и AY. Тогда пятиугольник APUQV — сечение, площадь которого надо найти.
Треугольники C 1 UQ и CYQ равны, откуда CY = C 1 U = 1.
Треугольники AYB и VYC подобны, откуда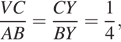 
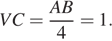Четырёхугольник APUY — равнобедренная трапеция, в которой
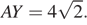
Треугольник QYV — равносторонний состороной 
нетрудно вычислить, что его площадь 
Вычислим высоту трапеции APUY,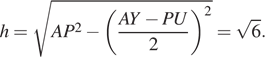 
Таким образом, её площадь 
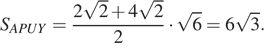Значит, искомая площадь равна 
Ответ: 
13. В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 стороны основания равны 5, а боковые рёбра равны 11.
а) Докажите, что прямые CA 1 и C 1 D 1 перпендикулярны.
б) Найдите площадь сечения призмы плоскостью, проходящей через вершины C, A 1 и F 1.
Решение.
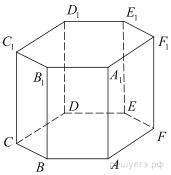а) Поскольку ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 — правильная шестиугольная призма, то ABCDEF — правильный шестиугольник. Тогда ∠ CBA = 120°. По теореме косинусов имеем 
Заметим, что A 1 A ⊥ (ABC), следовательно, AA 1 ⊥ CA. По теореме Пифагора CA 1 = 14.
Поскольку ABCDEF — правильный шестиугольник, DA = 2 AB = 10. Тогда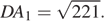 
По теореме, обратной теореме Пифагора, треугольник CA 1 D — прямоугольный. Тогда CD ⊥ CA 1. Поскольку С 1 D 1|| CD, имеем C 1 D 1 ⊥ CA 1.
б) Поскольку ABCDEF — правильный шестиугольник, AC ⊥ CD, поэтому A 1 CA — угол между искомым сечением и плоскостью ABCDEF. Так как A 1 A ⊥ CA, 
Площадь шестиугольника равна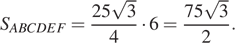 
Тогда площадь искомого сечения равна 105.
Ответ: б) 105.
|
|
14. Точки P и Q — середины рёбер AD и CC 1 куба ABCDA 1 B 1 C 1 D 1 соответственно.
а) Докажите, что прямые B 1 P и QB перпендикулярны.
б) Найдите площадь сечения куба плоскостью, проходящей через точку P и перпендикулярной прямой BQ, если ребро куба равно 10.
Решение.
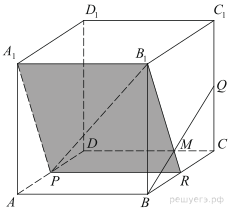а) Проведём отрезок 
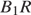, параллельный 
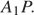Пусть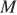 
— точка пересечения отрезков 
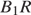и 
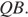Треугольник 
прямоугольный с прямым углом при вершине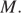 
Это следует из равенства треугольников 
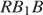и 
Значит, прямые 
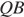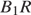и перпендикулярны. Прямые 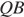и 
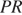перпендикулярны, так как прямая 
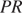перпендикулярна плоскости 
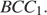Поэтому прямая 
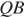перпендикулярна плоскости 
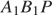, и, следовательно, прямая 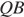перпендикулярна прямой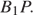 
б) Указанное сечение — прямоугольник 
Его площадь равна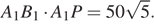 
Ответ: б)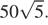 
15. Дана правильная четырехугольная призма ABCDA 1 B 1 C 1 D 1. На ребре AA 1 отмечена точка K так, что AK: KA 1 = 1: 2. Плоскость α проходит через точки B и K параллельно прямой AC. Эта плоскость пересекает ребро DD 1 в точке M.
а) Докажите, что MD: MD 1 = 2: 1.
б) Найдите площадь сечения, если AB = 4, AA 1 = 6.
Решение.
а) Проведём в прямоугольнике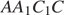 
отрезок KL параллельно AC. Заметим, что плоскость KBL параллельна прямой AC по признаку параллельности прямой и плоскости. Поэтому KBL — плоскость сечения. Плоскость сечения пересекает параллельные грани призмы по параллельным отрезкам. Проведём отрезок LM параллельно BK, проведем отрезок KM. Полученный четырёхугольник BLMK — искомое сечение. (См. Правила в конце пояснения.)
Из равенства АК = LC следует, что CL: LC 1 = 1: 2. В силу параллельности прямых KB и ML получаем, что DM = 2 LC, а тогда DM: MD 1 = 2: 1. Это и требовалось доказать.
б) Заметим, что по теореме о трех перпендикулярах прямые BM и AC перпендикулярны, а значит, прямые BM и KL перпендикулярны. Площадь четырехугольника, диагонали которого взаимно перпендикулярны, равна половине произведения диагоналей. Найдем их: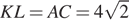 
как диагональ квадрата, лежащего в основании призмы, 
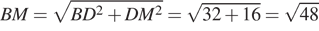по теореме Пифагора. Тогда
|
|
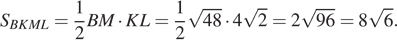
Ответ: б)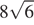 
.