Сечения многогранников. Задача № 14.
1. В основании правильной треугольной призмы ABCA 1 B 1 C 1 лежит треугольник со стороной 6. Высота призмы равна 4. Точка N — середина ребра A 1 C 1.
а) Постройте сечение призмы плоскостью BAN.
б) Найдите периметр этого сечения.
Решение.

а) Проведём через точку N прямую, параллельную прямой AB, до пересечения с прямой B 1 C 1 в точке K. Трапеция ABKN — искомое сечение.
б) Имеем A 1 N = 3, так как точка N — середина ребра A 1 C 1. Значит, 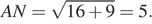 Аналогично BK = 5.
Аналогично BK = 5.
Далее NK = 3, как средняя линия треугольника A 1 B 1 C 1. Следовательно, искомый периметр сечения равен 6 + 5 + 5 + 3 = 19.
Ответ: 19.
2. В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.
а) Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.
б) Найдите площадь сечения.
Решение.
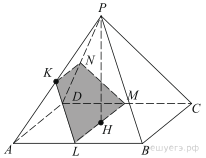
а) В плоскости ABP через точку K проведем прямую, параллельную прямой PB до пересечения ее с прямой AB в точке L — середине AB. В основании ABCD через точку L проведем прямую, параллельную прямой BC до пересечения ее с ребром СD в точке M — его середине. По признаку параллельности прямой и плоскости плоскость KLM параллельна прямым PB и BC. Прямая LM параллельна прямой AD, следовательно, она параллельна плоскости APD, а, значит, плоскость KLM пересекает плоскость APD по прямой, параллельной LM и пересекает ребро PD в его середине N.
Таким образом, искомое сечение ― трапеция KLMN.
б) Отрезки KL и MN равны, как средние линии равных правильных треугольников ABP и DCP, а отрезок LM ― средняя линия квадрата ABCD, следовательно, построенное сечение ― равнобедренная трапеция, в которой LM = 4, 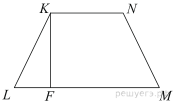 KL = KN = MN = 2. Проведем высоту KF этой трапеции. Тогда
KL = KN = MN = 2. Проведем высоту KF этой трапеции. Тогда  и из прямоугольного треугольника KLF находим
и из прямоугольного треугольника KLF находим 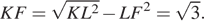
Окончательно получаем 
Ответ: 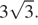
3. На ребре AA 1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 взята точка E так, что A 1 E = 6 EA. Точка T — середина ребра B 1 C 1. Известно, что  AD = 12, AA 1 = 14.
AD = 12, AA 1 = 14.
а) Докажите, что плоскость ETD 1 делит ребро BB 1 в отношении 4: 3.
б) Найдите площадь сечения параллелепипеда плоскостью ETD 1.
Решение.
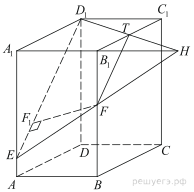 а) Проведём отрезок
а) Проведём отрезок 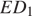 и в плоскости грани
и в плоскости грани  проведём через точку
проведём через точку 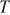 прямую, параллельную
прямую, параллельную  Эта прямая пересечёт ребро
Эта прямая пересечёт ребро 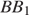 в точке
в точке 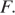 Точка
Точка 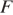 лежит в плоскости
лежит в плоскости  Треугольники
Треугольники  и
и 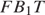 подобны. Следовательно,
подобны. Следовательно,
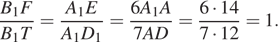
Таким образом, 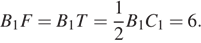 Тогда
Тогда  и
и 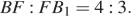
б) Четырёхугольник 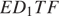 — сечение параллелепипеда плоскостью
— сечение параллелепипеда плоскостью  Поскольку стороны
Поскольку стороны 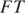 и
и  параллельны, но не равны. Четырёхугольник
параллельны, но не равны. Четырёхугольник 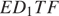 — трапеция. Продолжим боковые стороны
— трапеция. Продолжим боковые стороны  и
и 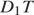 до пересечения в точке
до пересечения в точке  Точка
Точка 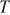 — середина
— середина 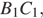 поэтому отрезок
поэтому отрезок 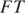 — средняя линия треугольника
— средняя линия треугольника  Из равенства треугольников
Из равенства треугольников 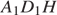 и
и 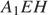 получаем
получаем 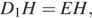 откуда
откуда  то есть трапеция
то есть трапеция  — равнобедренная.
— равнобедренная.
Найдём стороны трапеции:

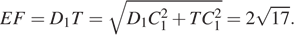
Высота равнобедренной трапеции 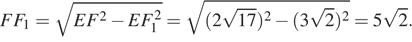
Тогда 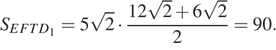
Ответ: б) 90.
4. На ребре AA 1 прямоугольного параллелепипеда ABCDA 1 B 1 C 1 D 1 взята точка E так, что A 1 E: EA = 5: 3, на ребре BB 1 — точка F так, что B 1 F: FB = 5: 11, а точка T − середина ребра B 1 C 1. Известно, что  AD = 10, AA 1 = 16.
AD = 10, AA 1 = 16.
а) Докажите, что плоскость EFT проходит через вершину D 1.
б) Найдите площадь сечения параллелепипеда плоскостью EFT.
Решение.
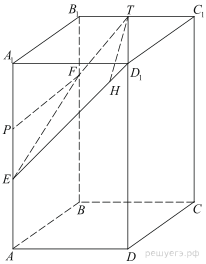 а) Плоскость EFT пересекает грани BB 1 C 1 C и AA 1 D 1 D по параллельным отрезкам.
а) Плоскость EFT пересекает грани BB 1 C 1 C и AA 1 D 1 D по параллельным отрезкам.
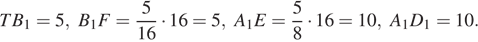
Значит, треугольники D 1 A 1 E и TB 1 F подобны, причём прямые D 1 A 1 и B 1 C 1 параллельны, прямые A 1 E и B 1 F тоже параллельны. Поэтому прямые ED 1 и FT также параллельны. Если плоскость EFT не проходит через точку D 1, то получается, что в плоскости AA 1 D 1 D через точку E проходят две различные прямые, параллельные прямой FT. Получили противоречие.
б) Сечение параллелепипеда плоскостью EFT — трапеция. Проведём через точку F прямую, параллельную прямой AB. Получим точку P на ребре AA 1.
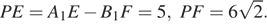
Тогда
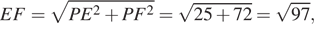
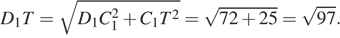
Следовательно, EF = D 1 T, и трапеция EFTD 1 равнобедренная. Проведём в ней высоту TH.


Тогда 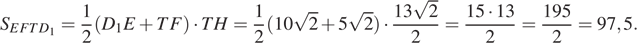
Ответ: б) 97,5.
5. Основанием прямой четырехугольной призмы ABCDA'B'C'D' является квадрат ABCD со стороной 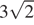 , высота призмы равна
, высота призмы равна  Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
Точка K — середина ребра BB'. Через точки K и С' проведена плоскость α, параллельная прямой BD'.
а) Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.
б) Найдите периметр треугольника, являющегося сечением призмы плоскостью α.
Решение.
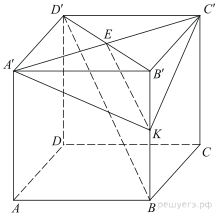 а) Проведём KE — среднюю линию треугольника BB'D'. E — середина B'D', следовательно, точка пересечения диагоналей верхнего основания и сечение содержит диагональ A'C'. Треугольник A'C'K является искомым сечением по признаку параллельности прямой и плоскости.
а) Проведём KE — среднюю линию треугольника BB'D'. E — середина B'D', следовательно, точка пересечения диагоналей верхнего основания и сечение содержит диагональ A'C'. Треугольник A'C'K является искомым сечением по признаку параллельности прямой и плоскости.
Прямоугольные треугольники A'B'K и С'B'K равны по двум катетам, поэтому A'K = С'K, следовательно, треугольник A'C'K — равнобедренный.
б) Далее имеем:


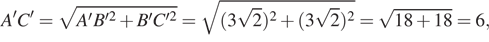

Ответ: б) 16.
6. В правильной треугольной пирамиде SABC сторона основания AB равна 12, а боковое ребро SA равно 13. Точки M и N — середины рёбер SA и SB соответственно. Плоскость α содержит прямую MN и перпендикулярна плоскости основания пирамиды.
а) Докажите, что плоскость α делит медиану CE основания в отношении 5: 1, считая от точки C.
б) Найдите площадь многоугольника, являющегося сечением пирамиды SABC плоскостью α.
Решение.
 а) Прямая MN параллельна плоскости ABC, поэтому сечение пересекает плоскость ABC по прямой PQ, параллельной MN. Рассмотрим плоскость SCE. Пусть K — точка пересечения этой плоскости и прямой MN, L — точка пересечения этой плоскости и прямой PQ, O — центр основания пирамиды. Плоскости SCE и MNQ перпендикулярна плоскости ABC, поэтому прямая KL перпендикулярна плоскости ABC, а значит, параллельна прямой SO. Поскольку MN — средняя линия треугольника ASB, точка K является серединой ES. Значит, L — середина EO. Медиана CE треугольника ABC делится точкой O в отношении 2: 1. Значит, CL: LE = 5: 1.
а) Прямая MN параллельна плоскости ABC, поэтому сечение пересекает плоскость ABC по прямой PQ, параллельной MN. Рассмотрим плоскость SCE. Пусть K — точка пересечения этой плоскости и прямой MN, L — точка пересечения этой плоскости и прямой PQ, O — центр основания пирамиды. Плоскости SCE и MNQ перпендикулярна плоскости ABC, поэтому прямая KL перпендикулярна плоскости ABC, а значит, параллельна прямой SO. Поскольку MN — средняя линия треугольника ASB, точка K является серединой ES. Значит, L — середина EO. Медиана CE треугольника ABC делится точкой O в отношении 2: 1. Значит, CL: LE = 5: 1.
б) В трапеции MNQP имеем:
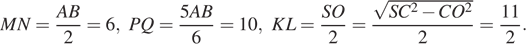
Значит, площадь трапеции MNPQ равна 
Ответ: б) 44.
7. Дана правильная призма ABCA 1 B 1 C 1, у которой стороны основания AB = 4, а боковое ребро AA 1 = 9. Точка M — середина ребра AC, а на ребре AA 1 взята точка T так, что AT = 5.
а) Докажите, что плоскость BB 1 M делит отрезок C 1 T пополам.
б) Плоскость BTC 1 делит отрезок MB 1 на две части. Найдите длину меньшей из них.
Решение.

а) Отметим точку  — середину
— середину  Очевидно,
Очевидно, 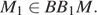 Проведем
Проведем  Это будет прямая, содржащая среднюю линию треугольника
Это будет прямая, содржащая среднюю линию треугольника 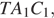 так как
так как  и проходит через середину
и проходит через середину 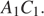 Значит, она проходит и через середину
Значит, она проходит и через середину 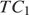 (назовем ее K), что и требовалось доказать (эта точка и есть точка пересечения данных прямой и плоскости)
(назовем ее K), что и требовалось доказать (эта точка и есть точка пересечения данных прямой и плоскости)
б) Рассмотрим плоскость  Отрезок BK лежит в ней и в плоскости
Отрезок BK лежит в ней и в плоскости 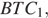 поэтому надо узнать, как отрезок BK делит отрезок
поэтому надо узнать, как отрезок BK делит отрезок  — диагональ прямоугольника
— диагональ прямоугольника 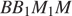 со сторонами
со сторонами 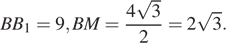 При этом
При этом 
Пусть O точка пересечения BK и  Тогда
Тогда
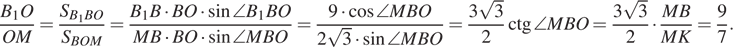
Поэтому 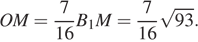
Ответ: б) 
8. Дана правильная шестиугольная пирамида SABCDEF с вершиной S.
а) Докажите, что плоскость, проходящая через середины рёбер SA и SD и вершину C, делит апофему грани ASB в отношении 2: 1, считая от вершины S.
б) Найдите отношение, в котором плоскость, проходящая через середины рёбер SA и SD и вершину C, делит ребро SF, считая от вершины S.
Решение.

а) Обозначим за M, N середины ребер SA и SD. Поскольку MN — средняя линия треугольника SAD, то  поэтому точка B также лежит в данной плоскости. Поэтому с гранью ABS данная плоскость пересекается по прямой BM — медиане треугольника SAB. Она делит его медиану SQ (Q — середина AB) в отношении 2: 1 считая от вершины.
поэтому точка B также лежит в данной плоскости. Поэтому с гранью ABS данная плоскость пересекается по прямой BM — медиане треугольника SAB. Она делит его медиану SQ (Q — середина AB) в отношении 2: 1 считая от вершины.
б) Пусть  Поскольку MN — средняя линия треугольника SAD, она делит отрезок SK пополам, то есть T — середина SK. Ясно, что T лежит в данной плоскости.
Поскольку MN — средняя линия треугольника SAD, она делит отрезок SK пополам, то есть T — середина SK. Ясно, что T лежит в данной плоскости.
Рассмотрим теперь треугольник SBF. В нем проведена медиана SK и отмечена ее середина T. В данной плоскости лежит прямая BT, пересекающая SF в точке W. Осталось выяснить местоположение точки W.
Напишем теорему Менелая для треугольника FSK и прямой  , откуда
, откуда 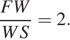
Ответ: 1: 2.
9. Площадь основания правильной четырёхугольной пирамиды SABCD равна 64.
а) Постройте прямую пересечения плоскости SAC и плоскости, проходящей через вершину S этой пирамиды, середину стороны АВ и центр основания.
б) Найдите площадь боковой поверхности этой пирамиды, если площадь сечения пирамиды плоскостью SAC равна 64.
Решение.
Сторона основания пирамиды равна 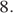 Тогда диагональ основания
Тогда диагональ основания 
а) Пусть  — высота пирамиды. Тогда
— высота пирамиды. Тогда  — середина основания пирамиды. Значит,
— середина основания пирамиды. Значит,  — искомая прямая.
— искомая прямая.
б) Площадь сечения, проходящего через 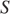 и диагональ
и диагональ  равна
равна  откуда
откуда  Пусть
Пусть  — высота грани
— высота грани 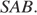 Тогда
Тогда

Следовательно,  Поэтому
Поэтому 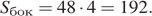
Ответ: 192.
10. В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 сторона основания AB равна 3, а боковое ребро 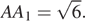 На рёбрах AB, A 1 D 1 и C 1 D 1 отмечены точки M, N и K соответственно, причём AM = A 1 N = C 1 K = 1.
На рёбрах AB, A 1 D 1 и C 1 D 1 отмечены точки M, N и K соответственно, причём AM = A 1 N = C 1 K = 1.
а) Пусть L — точка пересечения плоскости MNK с ребром BC. Докажите, что MNKL — квадрат.
б) Найдите площадь сечения призмы плоскостью MNK.
Решение.
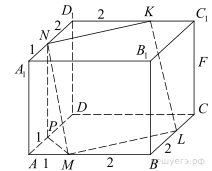 а) Плоскость MNK пересекает плоскости оснований ABCD и A 1 B 1 C 1 D 1 по параллельным прямым, следовательно, прямые NK и ML параллельны.
а) Плоскость MNK пересекает плоскости оснований ABCD и A 1 B 1 C 1 D 1 по параллельным прямым, следовательно, прямые NK и ML параллельны.
Отрезки NK и ML не только параллельны, но и равны, поскольку равны треугольники ND 1 K и MBL. Поэтому четырёхугольник NKLM — параллелограмм. Покажем, что его стороны перпендикулярны.
Пусть P — проекция точки N на плоскость нижнего основания, тогда  прямоугольные треугольники PAM и MBL равнобедренные, углы PMA и BML равны по 45°, а значит,
прямоугольные треугольники PAM и MBL равнобедренные, углы PMA и BML равны по 45°, а значит,  то есть прямые PM и ML перпендикулярны. Но PM является проекцией наклонной NM, поэтому стороны параллелограмма NM и ML перпендикулярны по теореме о трех перпендикулярах. Вычисления показывают, что
то есть прямые PM и ML перпендикулярны. Но PM является проекцией наклонной NM, поэтому стороны параллелограмма NM и ML перпендикулярны по теореме о трех перпендикулярах. Вычисления показывают, что 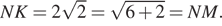
Тем самым, MNKL — квадрат.
б) Заметим, что косинус угла между плоскостью основания и плоскостью сечения равен 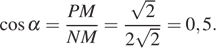 Площадь сечения связана с площадью проекции сечения на плоскость основания формулой
Площадь сечения связана с площадью проекции сечения на плоскость основания формулой 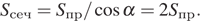 Площадь проекции равна разности площади лежащего в основании квадрата и двух равнобедренных прямоугольных треугольников с катетами 2. Тем самым, площадь проекции равна 9 − 4 = 5, а площадь сечения равна 10.
Площадь проекции равна разности площади лежащего в основании квадрата и двух равнобедренных прямоугольных треугольников с катетами 2. Тем самым, площадь проекции равна 9 − 4 = 5, а площадь сечения равна 10.
Ответ: а) доказано; б) 10.

Приведём другое решение.
а) Покажем, что стороны четырёхугольника MNKL равны и диагонали равны:

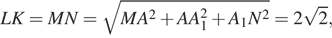
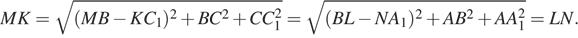
Поэтому MNKL — квадрат.
б) Пусть W — точка пересечения прямых NK и A 1 B 1. Тогда WA 1 = NA 1 как катеты равнобедренного прямоугольного треугольника. Пусть E — точка пересечения прямой WM с ребром AA 1. Прямоугольные треугольники WA 1 Е и EAM подобны, а их катеты MA и WA 1равны. Поэтому равны и другие катеты, а значит, Е — середина AA 1. Аналогично, плоскость MNK пересекает ребро CC 1 в его середине F. В прямоугольнике AEFC противоположные стороны равны, поэтому 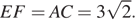
Сечение — шестиугольник MENKFL — состоит из двух равных трапеций ENKF и EMLF, причём прямая MN перпендикулярна их основаниям. Поэтому искомая площадь сечения равна
