Система регулирования уровня жидкости в резервуаре с самовыравниванием (рис. 9).
 |
| Рис. 9. Структура системы фаззи-регулирования уровня жидкости |
ОУ представлен идеальным интегрирующим звеном, которое охвачено нелинейной отрицательной обратной связью, соответствующей закону истечения жидкости из резервуара. Резервуар характеризуется коэффициентом 1/S, где S - площадь поверхности жидкости, м2. Подача жидкости в резервуар qn регулируется с помощью задвижки (3), степень открытия которой j пропорциональна qn.
В качестве управляющего воздействия у рассматривается скорость перемещения задвижки, т.е. у (t) = d (j(t))/ dt.
Если имеется возможность измерения скорости изменения уровня, то один из простейших алгоритмов управления может быть представлен в виде следующих пяти нечетких правил (рис. 10):
| 1. ЕСЛИ уровень нормальный (e1 = ZR), TO положение задвижки не изменять (у = ZR) ИЛИ 2. ЕСЛИ уровень низкий (e1 = РВ), ТО задвижку открывать быстро (у = РВ) ИЛИ 3. ЕСЛИ уровень высокий (e1 = NB), TO задвижку закрывать быстро (у = NB) ИЛИ 4. ЕСЛИ уровень нормальный (e1 = ZR) И он увеличивается (e2 = РВ), ТО задвижку закрывать медленно (у = NM) ИЛИ 5. ЕСЛИ уровень нормальный (e1 = ZR) И он уменьшается (e 2 = NB), ТО задвижку открывать медленно (у = РМ) | (35) |

| Рис. 10. Функции принадлежности для отклонения уровня e1 = h 3 - h (а), скорости его изменения e2 = dh / dt (б) и скорости перемещения задвижки у (в) |
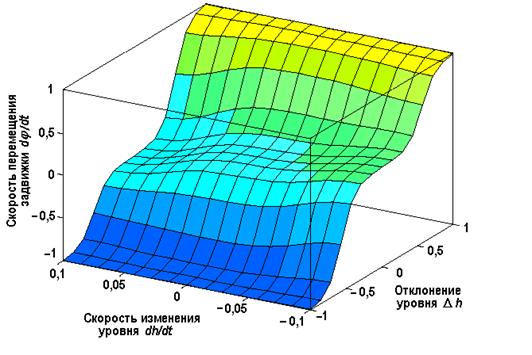
Соответствующие правилам (35) процедуры фаззификации и импликации проиллюстрированы на рис. 11 для конкретных значений e1 * и e2*. ФП управляющего воздействия определены по методу произведения (см. заштрихованные треугольники). Результирующее значение управляющего воздействия у * вычислено по формуле (27) как средневзвешенное значение для двух заштрихованных треугольников. На рис. 12 показано пространство управления, соответствующее правилам (35) выбранным ФП (см. рис.10) и принципу дефаззификации (27).
|
|
 |
| Рис. 11. Схема функционирования фаззи-регулятора |
Система управления положением тележки мостового крана. Объектом управления является механическая система, состоящая (рис. 13) из тележки с массой m т, груза с массой m г и привода. Данная колебательная система описывается уравнением состояния
| x ¢(t) = A x (t) + B y (t) | (36) |
И уравнением выхода
| X в (t) = C x (t) | (37) |
где x (t) - 4-мерный вектор состояния с компонентами: x 1(t) перемещение тележки, м; x 2(t) = x¢ 1(t) скорость ее перемещения, м/с; x 3(t) - угол отклонения груза, рад;
x 4(t) = x 3¢(t) - угловая скорость груза, рад/с; у (t) = u д(t) - управляющее воздействие - напряжение двигателя тележки, В; х в(t) = х 1(t) - выходная (измеряемая) переменная;

| (38) |
| а 23 = m 1 g / m т; а 43 = - (m т + m г) g / m т L; b 2 = k п/ m т; b 4 = - k п/ m т L; | (39) |
k п - передаточный коэффициент привода, Н/В. Общая цель управления объектом заключается в быстром и точном позиционировании тележки при минимальных колебательных движениях тележки и груза.
|
| Рис. 12. Пространство управления фаззи-регулятора уровня жидкости |
В качестве основной входной переменной регулятора (рис. 14) рассматривается отклонение положения тележки от заданного e = х вз- х в, а в качестве управляющего воздействия - напряжение u д, подаваемое на электропривод тележки. Причем, эти две переменные рассматриваются в дискретные моменты времени t = 1 D t, 2 D t; …, k D t; ….
|
|
 |
| Рис. 13. Тележка мостового крана как ОУ |
Для того, чтобы избежать больших колебаний и динамических перегрузок, в качестве выходной переменной регулятора принимается падение напряжения D u д(k) = D y (k), соответствующее интервалу дискретности D t, а в качестве второй входной переменной регулятора значение напряжения на предыдущем шаге, т. е. u (k - l).
Для обеих входных переменных фаззи-регулятора e(k) и u (k - 1), нормированных на интервале [1, +l], можно применить унифицированные треугольные и трапециевидные ФП, показанные на рис. 7, б, а для выходной D u д(k) – ФП в форме синглтонов.
Всю совокупность правил управления тележкой, сформулированных на основе знаний о динамике данного объекта, требованиях к его поведению, и выражающих определенную логику целенаправленных действий, можно представить в виде так называемой таблицы лингвистических правил (табл. 2).
Таблица 2