Практическое занятие № 39 «Действия с векторами»
Выполните:
1. Даны векторы 
={2; 5;0}, 
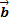={1; -1; 3}. Найти сумму, разность, косинус угла и векторное произведение.
2. Дана сила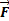 
=(1;3;7) и точки А(3;0;2), В(-1;1;0). Найти работу и модуль силы.
Практическое занятие № 40 «Скалярное произведение векторов»
Скалярное произведение двух векторов 
, заданных своими координатами, равно сумме произведений их одноименных координат, то есть
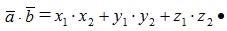
С помощью скалярного произведения векторов можно вычислить угол между ними. Если заданы два ненулевых вектора своими координатами , то косинус угла φ между ними:
Отсюда следует условие перпендикулярности ненулевых векторов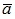 
и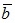 
Нахождение проекции вектора 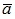на направление, заданное вектором 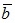, может осуществляться по формуле
С помощью скалярного произведения векторов находят работу постоянной силы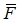 
на прямолинейном участке пути.
Предположим, что под действием постоянной силы 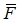материальная точка перемещается прямолинейно из положения А в положение B. Вектор силы 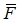образует угол φ с вектором перемещения 
(рис. 2.14). Физика утверждает, что работа силы 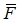при перемещении 
равна 
.
Следовательно, работа постоянной силы при прямолинейном перемещении точки ее приложения равна скалярному произведению вектора силы на вектор перемещения.
Пример № 1. С помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах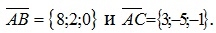 
Решение. Вычислим модули векторов и их скалярное произведение по теореме (2.3):
Отсюда согласно формуле (2.29) получим косинус искомого угла
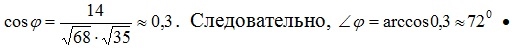
Пример № 2. Вычислить работу, произведенную силой 
, если точка ее приложения перемещается прямолинейно из положения A (2;4;6) в положение A (4;2;7). Под каким углом к AB направлена сила ?
Решение. Находим вектор перемещения, вычитая из координат его конца координаты начала
. По формуле 
(единиц работы).
Угол φ между 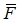и находим по формуле (2.29), то есть
Выполнить:
1. С помощью скалярного произведения векторов найти угол при вершине A параллелограмма ABCD, построенного на векторах
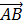={7;0;3}, 
={2;-1; -2}
2. Вычислить работу, произведенную силой 
{1; 2; 3} если точка ее приложения перемещается прямолинейно из положения A (2;4;6) в положение A (4;2;7). Под каким углом к AB направлена сила ?
Практическое занятие № 41 «Векторное уравнение прямой и плоскости
1. Составить уравнение прямой с угловым коэффициентом 
, если известно, что точка 
принадлежит данной прямой.
Решение: Уравнение прямой составим по формуле 
. В данном случае:
Ответ: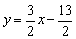 
2.Составить уравнение прямой по двум точкам 
.
Решение: Используем формулу:
Причёсываем знаменатели:
И перетасовываем колоду:
Именно сейчас удобно избавиться от дробных чисел. В данном случае нужно умножить обе части на 6:
Раскрываем скобки и доводим уравнение до ума:
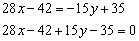
Ответ: 
3.Составить уравнение плоскости по точкам 
.
Решение: составим уравнение плоскости по трём точкам. Используем формулу:
Вот теперь и аналитически видно, что всё дело свелось к координатам двух векторов. Раскрываем определитель по первому столбцу, находим уравнение плоскости:
5(х-1)-(у+2)+3z=0
5x-y+3z-7=0- уравнение плоскости.
Выполнить:
1. Составить уравнение прямой с угловым коэффициентом к=5, если известно, что точка А(4; -6) принадлежит данной прямой.
2. Составить уравнение прямой по двум точкам А(3;2), В(4;7).
3. Составить уравнение плоскости по точкам А(1;0;3)., В(0;-1;2), С(1;2;3)