СТАТИСТИЧЕСКИЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ ДВУМЕРНОГО

СЛУЧАЙНОГО ВЕКТОРА

Пример1. Вычислить выборочные средние , , несмещенные оценки дисперсий , 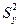и коэффициент корреляции для выборки

 

 

Решение. Для расчетов воспользуемся формулами

 

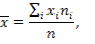
, (4)

 

 

 

где n – объем выборки, n _ij– частота появления пары элементов (x _i, y _j) выборки; n _i – частота появления элемента x _i (при любом y); n _j – частота появления элемента y (при любом x).

В рассматриваемом примере среди значений x _i, y _j нет повторяющихся, поэтому

 

 

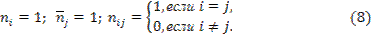
Вычисления удобно свести в таблицу.

 

Таблица 8

i

 

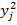
Последний столбец таблицы служит для контроля вычислений с помощью тождества

 

(В данном случае: 530 = 334 + 2∙86 + 24).

Используя данные из последней строки и учитывая (8),по формулам (4)–(7)получаем

 

 

 

 

Пример 2. В табл. 9приведены результаты измерений двух физических величин в ходе некоторого эксперимента

 

Таблица 9

Вычислить средние, несмещенные оценки дисперсий и коэффициента корреляции, предварительно сгруппировав выборку и составив корреляционную таблицу.

 

Решение. Определим размах выборки по х и по у

 

 

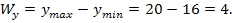
В данном случае для группировки элементов выборки удобно использовать четыре интервала по х и два интервала по у. Определим длины интервалов группировки

 

 

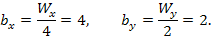
Группировку выборки можно производить по диаграмме рассеивания (см. рис. 9). Для построения этой диаграммы нанесем элементы выборки (x _i, y _j) в виде точек на плоскость с выбранной системой координат.

 

 

Рис. 9

 

Будем считать, что элементы выборки, которые попали на границу двух соседних прямоугольников, относятся к верхнему или к правому прямоугольнику, и составим корреляционную таблицу.

 

Таблица 10

y	x	46-50	50-54	54-58	58-62
16-18
18-20

Здесь x _i^*, y _j^* – означают середины интервалов группировки. В клетках таблицы записываются частоты (то есть число пар исходной выборки, попавших в данный прямоугольник) для каждого прямоугольника на диаграмме рассеивания.

Для вычисления искомых оценок параметров распределения по сгруппированной выборке можно использовать те же формулы (4)–(7),в которых x _i, y _jследует заменить на x _i^*, y _j^*, а 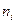, , – на частоты попадания элементов выборки в соответствующие интервалы , , .

Однако, если x _i^*, y _j^*достаточно велики, то для упрощения вычислений рекомендуется ввести вспомогательные случайные величины

 

где d _x, d _y–наиболее часто встречающиеся значения x _i^* и y _j^*.Найти их параметры распределения по формулам, аналогичным (4)–(7),а затем воспользоваться соотношениями

 

(11)

 

В заданном примере .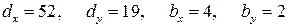

Результаты промежуточных вычислений представим в виде таблицы (табл. 11).

По формулам (4) - (7)используя найденные в таблице вспомогательные суммы 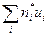, , , , 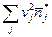и вычислив имеем

Таблица 11

xi*
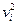
yj*	ui vj	-1
	-1						-10
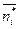
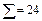
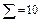
	-5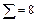

 

 

 

 

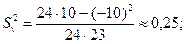
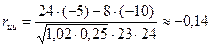
Возвращаясь к заданным случайным величинам, по формулам (11) получим

 

 

Пример 3. По выборке из примера 2 оценить параметры линейной регрессии X на Y и Y на X и составить уравнения прямых регрессии.

Решение. Уравнения прямых регрессии Y на X и X на Y были получены в курсе теории вероятностей и имеют вид

 

 

Заменяя в этих уравнениях числовые характеристики m_x, m_y, , , r_xy их статистическими оценками, получим

(12)

(13)

 

Подставляя в эти уравнения найденные в предыдущем примере значения , , S_x, S_y, r_xy имеем

 

 

Отсюда следует, что уравнения линейной регрессии Y на X и X на Y имеют соответственно вид

 

 

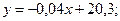
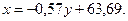
Отметим, что эти прямые пересекаются в точке (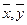). Угол между ними уменьшается при увеличении , а при = 1, прямые регрессии совпадают.

 

Решите примеры, используя данные своего варианта, приведенные в Приложении 2, табл. 1,2.

4. В ходе некоторого эксперимента были многократно измерены две физические величины X и Y. Результаты измерений записаны в таблицу. Обработайте результаты эксперимента по следующему плану:

1) постройте диаграмму рассеивания;

2) составьте корреляционную таблицу;

3) вычислите средние, несмещенные оценки дисперсий среднеквадратичных отклонений и оцените коэффициент корреляции;

4) составьте уравнения прямых регрессии и нанесите эти прямые на диаграмму рассеивания.

5. Вычислить выборочные средние , , несмещенные оценки дисперсий , 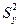и коэффициент корреляции для выборки, представленной в табл. 2 приложения 2.

 

ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

Интервальной называют оценку, которая определяется двумя числами — концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надежностью покрывает заданный параметр.

1. Интервальной оценкой с надежностью математического ожидания а нормально распределенного количественного признака по выборочной средней 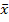при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал

,

Где =δ – точность оценки, n - объем выборки, t – значение аргумента функции Лапласа Ф(t) при котором Ф(t)=γ/2.

2. При неизвестном σ (и объеме выборки n<30)

,

где s - «исправленное» выборочное среднее квадратическое отклонение, t находят по таблице квантилей распределения Стьюдента по заданным n и γ.

Пример 1. Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания a нормально распределенного признака X генеральной совокупности, если генеральное среднее квадратичное отклонение σ = 5, выборочная средняя 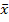= 14 и объем выборки n = 25.

Решение. Требуется найти доверительный интервал

,

Все величины, кроме t, известны. Найдем t из соотношения Ф(t) = 0,95/2=0,475. По таблице находим t = 1,96. Подставив t = 1,96, 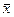= 14, σ = 5, n = 25, окончательно получим искомый доверительный интервал 12,04 < a < 15,96.

Пример 2. Из генеральной совокупности извлечена выборка объема n = 10, представленная в табл. 12.

 

Таблица 12

варианта xi	-2
частота ni

 

Оценить с надежностью 0,95 математическое ожидание а нормально распределенного признака генеральной совокупности по выборочной средней при помощи доверительного интервала.

Решение. Выборочную среднюю и «исправленное» среднее квадратичное отклонение найдем соответственно по формулам:

, .

Подставив в эти формулы данные задачи, получим 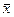= 2, s = 2,4. Найдем t_γ. Пользуясь таблицей, по γ = 0,95 и n = 10 находим t_γ = 2,26. Найдем искомый доверительный интервал:

.

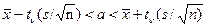Подставляя в эти формулы данные задачи, получим 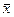= 2, t_γ = 2,26, s = 2,4, n= 10, получим искомый доверительный интервал 0,3< a < 3,7, покрывающий неизвестное математическое ожидание а с надежностью 0,95.

3. Пусть известно, что контролируемое напряжение в задаче 10 параграфа 1 распределено по нормальному закону. Найти доверительный интервал для оценки с надежностью 0,99 неизвестного математического ожидания a.