Оценку «зачтено» выставляется работам, которые отвечают одному из следующих требований:
1. контрольная работа выполнена полностью, в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непонимания материала);
2. контрольная работа выполнена полностью, но обоснования шагов решения недостаточны, допущена одна негрубая ошибка или два-три недочета в выкладках, если эти виды работы не являлись специальным объектом проверки;
3. в контрольной работе допущена одна достаточно грубая ошибка или более двух-трех недочетов в выкладках, но студент владеет обязательными умениями по проверяемой теме.
Оценка «незачтено» ставится, если студент показал полное отсутствие обязательных знаний и умений по проверяемой теме.
К грубым ошибкам относятся ошибки, которые обнаруживают незнание студентом формул, правил, основных свойств и неумение их применять, незнание приемов решения заданий, а также вычислительные ошибки, если они не являются опиской.
К негрубым ошибкам относятся вычислительные ошибки, если они являются опиской.
К недочетам относятся нерациональное решение, описки, недостаточность или отсутствие пояснений, обоснований в решении задания.
Студент, контрольная работа которого не получила положительную оценку, не допускается к сдаче экзамена по дисциплине «Статистика».
Контрольная работа по дисциплине «Статистика»
1.
2.
Методические указания к выполнению контрольной работы
Задача 1.
При решении задачи №1 необходимо выделить две группы территорий и охарактеризовать их особенности с помощью системы показателей. Для проведения группировки рекомендуется расположить территории по возрастанию группировочного признака, указанного в условии, и отделить территории одной группы от другой.
|
|
Для построения системы показателей выполняется расчёт итоговых значений только первичных признаков по каждой группе и по всему множеству. Система показателей включает в себя: а)число территорий в каждой группе и, в том числе, в % к итогу; б)средние значения первичных признаков в расчёте на 1 территоррию; в)относительные характеристики как соотношение суммарных значений двух первичных признаков. Например:
Стоимость ВРВ на 1-го занятого в экономике, тыс. руб.=
= ∑ стоимость ВРП: ∑ численность занятых в экономике.
Результаты группировки и сводки оформляются в заключительной таблице. Сравнительный анализ полученных результатов выполняется по группам и между группами, краткие выводы излагаются в аналитической записке.
Задача 2.
При решении задачи №2 необходимо, в первую очередь, определить единицу изучаемого множества, её первичные и вторичные признаки. По первичным признакам расчёт общей средней выполняется по схеме простой арифметической. Для вторичного признака определяем схему расчёта его индивидуальных значений и выражаем неизвестный по условию задачи признак через известные, используя их буквенные обозначения. Полученную расчётную схему используем для определения общей средней.
Например, по условию задачи по нескольким предприятиям известна стоимость продукции — Qi и выработка продукции на 1-го работника — Wi. Так как признак Qi является первичным, значение его общей средней рассчитаем по простой арифметической:
|
|
Признак Wi — вторичный, его индивидуальные значения получены по формуле Стоимость продукции: Численность работников.
Численность работников по условию неизвестна, но её можно найти, если выразить через Стоимость продукции и Выработку на 1-го работника, то есть:
Тогда общая средняя будет рассчитана следующим образом:
Здесь использована средняя гармоническая взвешенная, а весом является первичный признак Qi — Стоимость продукции. Следует помнить, что весом всегда выступает первичный признак, в какой бы сложной форме он ни присутствовал в используемом расчёте.
Задача 3.
При решении задачи №3 необходимо определить границы «открытых» интервалов, применяя величину интервала iх, которая для всех групп остаётся одинаковой.
Далее выполняется расчёт серединного значения признака в каждом интервале как полусуммы его максимального и минимального значений:
Расчёт показателей вариации основан на использовании формул для вариационного ряда, то есть, в расчёте участвуют частоты — fi. Необходимо рассчитать среднее значение признака — 
, среднее квадратическое отклонение — σx, коэффициент вариации — Vx, коэффициент асимметрии — 
, значение моды — Mo и медианы Me. Здесь m3 — центральный момент третьего порядка: 
Вариационный ряд иллюстрируют полигон распределения частот и гистограмма. При построении полигона ломаная линия должна пересечь ось 0Х в середине «нулевого» интервала и «К+1» интервала, которые имеют нулевые частоты: f0 = fk+1 = 0, иначе площади полигона и гистограммы не будут равны.
|
|
Задача 4.
В задаче №4 предполагается выполнить расчёт абсолютных и нормированных показателей различий 2-х структур. Средние арифметические показатели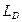 
, 
определяются по следующим формулам: 
; 
. Здесь 
и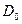 
— показатели удельного веса, оценивающие отчётную и базисную структуры и выраженные в процентах: 
. Показатель 
определяет на сколько процентов в среднем отличается удельный вес каждой группы отчётной и базисной структуры, а оценка 
показывает сколько процентных пунктов составляют фактические различия двух структур от величины их предельных различий, составляющих 200%.
Средние квадратические показатели различий 2-х структур характеризуются особым порядком расчёта: здесь используется форма квадратической средней:
; 
Коэффициент Гатева принадлежит к группе квадратических нормированных характеристик и показывает сколько процентных пунктов составляют фактические различия 2-х структур от их возможных различий:
Задача 5.
Решение задачи №5 начинается с выяснения природы изучаемых явлений: относятся они к категории соизмеримых или несоизмеримых. Для несоизмеримых явлений характерна различная физическая форма и разное потребительское назначение.
Затем анализируется связь признаков, значения которых приведены в условии задачи. При использовании индексов обычно предполагается наличие жёсткой мультипликативной связи признака-результата и признаков-факторов: 
Например, зависимость товарооборота — 
от физического объёма реализованных товаров разного вида — 
и от цен за единицу товара каждого вида — 
. Следует определить, какой из признаков данной системы отсутствует в условии задачи и рассчитать его значения в базисном и отчётном периодах. Если, например, отсутствует , тогда 
; если отсутствует , тогда 
; если отсутствует 
, тогда 
.
Например, для оценки происшедших изменений признаков W, Q и P выберем систему индексов для анализа несоизмеримых явлений: систему индивидуальных индексов — 
и систему сводных (агрегатных) индексов — 
.
Расчёт сводного индекса признака-результата — W выполняется по схеме:
. Например, 
или 102,6%.
Уровень товарооборота в отчётном периоде составил в среднем 102,6% от его уровня в базисном периоде, то есть он увеличился в среднем на 2,6% (1,026⋅100%−100%=2,6%), что составило 5,2 например, млн. руб. (205,2−200,0=5,2 млн. руб.).
Сводный индекс первичного признака-фактора Q рассчитаем по схеме:
. Следует выполнить расчёт Wусловное = Q1*P0. и определить величину 
.
В нашем примере: 
или 108,0%. Уровень отчётных значений физического объёма продаж — 
составил от уровня его базисных значений в среднем 108%. Значения физического объёма — 
за отчётный период увеличились в среднем на 8%, это привело к увеличению значений товарооборота — W на 16 млн. руб.
Сводный индекс вторичного признака-фактора P рассчитаем по схеме:
.
В нашем примере: 
или 95,0%. Уровень цен — P1 на товары разного вида в отчётном периоде составил в среднем 95% от уровня их значений в базисном периоде, то есть цены за отчётный период уменьшились в среднем 5%, это привело к уменьшению значений товарооборота — W на 10,8 тыс.руб.
Представим результаты в виде системы индексов в относительной форме: 
или 1,026 =1,080⋅0,950. Из двух факторов, влияющих на результат, один изменился в большей мере: на + 8% (
или 8% прироста), а другой — в меньшей степени: на –5% (
или 95%, то есть прирост составил – 5%).
Представим в виде системы величину абсолютных размеров прироста результата за счёт каждого фактора:
или + 5,2 млн. руб. = + 16,0 млн.руб. + (–10,8) млн.руб.
В нашем примере, в результате увеличения физического объёма продаж товарооборот увеличился на 16,0 млн.руб., а за счёт снижения цен товарооборот уменьшился на 10,8 млн.руб. В целом же, совместное влияние обоих факторов привело к увеличению товарооборота на 5,2 млн.руб. Это было вызвано более сильным воздействием возросшего физического объёма продаж.
Задача 6.
При решении задачи №6 необходимо по информации об изменениях цен рассчитать индивидуальные индексы цен: если по условию задачи известны значения 
, тогда 
. Для расчёта общего индекса цен воспользуемся схемами расчёта Пааше: 
и Ласпейреса: 
. Для их расчёта по условию задачи необходимо использовать форму сводного индекса как среднего из индивидуальных, применяя либо гармоническую взвешенную, либо арифметическую взвешенную. В первом случае весом выступают отчётные значения признака-результата — W1. В другом случае, весом выступают базисные значения признака-результата — W0. Исходная расчётная формула может быть упрощена, если вместо значений W1 и W0 использовать в качестве веса показатели отчётной или базисной структуры признака-результата, то есть 
или 
. В этом случае расчётные схемы будут иметь вид:
.
В данном случае для расчёта сводного индекса цен необходимо единицу разделить на полученный результат, который представляет собой величину, обратную значению сводного индекса цен. В расчёте участвует отчётная структура потребления, в которой нашла отражение склонность населения к потреблению более дешёвых товаров и тех, на которые цены снизились в меньшей степени, то есть здесь учтена эластичность потребительского рынка.
.
Индекс Ласпейреса получен как средний арифметический из индивидуальных индексов цен, скорректированных на базисную структуру признака-результата. Индекс цен Ласпейреса (в отличие от индекса цен Пааше) не учитывает эластичность потребительского рынка. Различия в значениях индексов цен Пааше и Ласпейреса, которые известны как эффект Гершенкрона, объясняются указанными особенностями их построения.
Задача 7.
Решение задачи №7 начинается с выяснения природы изучаемых явлений: относятся они к категории соизмеримых или несоизмеримых. Соизмеримые явления характеризуются одинаковой физической формой и общими, едиными потребительскими свойствами, назначением и использованием. Например, необходимо изучить зависимость и изменения значений признаков: W — стоимость произведённой продукции; T — численность работников; S — выработка продукции в среднем на 1-го работника. Зависимость признаков выражается соотношением: Wi = Ti⋅ Si.
Отсутствующие в условии задачи значения признаков у изучаемых единиц совокупности необходимо рассчитать: неизвестные значения Wi = Ti⋅ Si; неизвестные значения 
; неизвестные значения 
.
Для анализа соизмеримых явлений используются система сводных индексов: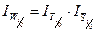 
.
В условии задачи предлагается рассмотреть ту часть системы, где более подробно анализируются факторы изменения среднего значения вторичного признака и рассчитать индекс переменного состава — 
, индекс постоянного состава — 
и индекс структурных сдвигов — 
, то есть систему сводных индексов в относительной форме:
.
Для расчёта указанных индексов необходимы значения общей средней выработки, которые определяются по формуле: 
.
Индекс переменного состава или индекс общей средней рассчитаем по схеме:
.
В нашем примере 
(тыс.руб.);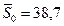 
(тыс.руб.), тогда 
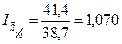или 107,0%. Общая средняя выработка отчётного периода оставила от уровня базисного периода 107%, то есть средняя выработка возросла на 7%
Индекс постоянного состава или индекс собственно выработки покажет как изменилась общая средняя под влиянием изменений индивидуальных значений вторичного признака; его значение определим по схеме:
.
В расчёте участвует условная средняя выработка, значение которой определяется на основе условной величины результата – условной стоимости продукции; её необходимо предварительно рассчитать.
В нашем примере 
(тыс.руб.). Тогда: 
или 104,3%.
Индекс постоянного состава показывает, что в результате изменения индивидуальной выработки работников общая средняя выработка в отчётном периоде составила 104,3%, то есть возросла на 4,3%.
Индекс структурных сдвигов оценивает изменения общей средней под влиянием изменений удельного веса единиц с высокими и низкими значениями вторичного признака-фактора.
или 102,6%.
В результате увеличения удельного веса работников с высоким уровнем выработки и уменьшения удельного веса работников с низким уровнем общая средняя выработка составила 102,6% от базисного уровня, то есть возросла на 2,6%. Если бы в структуре произошли противоположные изменения, тогда бы общая средняя уменьшилась, а величина индекса структуры была бы меньше единицы.
Представим полученные результаты в виде системы индексов в относительной форме:
; в нашем примере 1,070 = 1,043⋅1,026.
Увеличение общей средней выработки на 7% произошло в результате увеличения индивидуальной выработки на 4,3% и на 2,6% за счёт изменений в структуре работников. Из двух факторов, повлиявших на увеличение общей средней выработки, изменения индивидуальной выработки были более значительными, а их влияние на увеличение общей средней — более сильным, чем влияние изменений в структуре работников.
Задача 8.
В задаче №8 необходимо сформировать случайную бесповторную выборку, рассчитать по ней значение средней (
) и доли (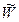
), их ошибки (
и 
) и построить доверительный интервал (
и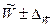 
) возможных значений генеральной средней и генеральной доли.
При формировании выборочного множества используют либо механический отбор, либо жеребьёвку, обычно применяя таблицу случайных чисел (ТСЧ). Механический отбор предполагает расчёт шага отбора — 
; где 
— число единиц генерального множества; 
— число единиц выборочной совокупности. Порядковый номер первого элемента выбирается случайно, например, по ТСЧ. Если первый элемент выборки имеет номер 7, то при h = 15 в выборку будут отобраны единицы с номерами 7, 22, 37, 52, 67 и т.д.
При использовании ТСЧ устанавливается и фиксируется в комментариях правило, по которому будут отбираться пятизначные числа и их используемые разряды. Например, отбираем числа, двигаясь слева направо по строке, начиная с ячейки первой графы первой строки. Из выбранных 5-тизначных чисел используем первую и вторую цифры. Фрагмент ТСЧ представлен в таблице 2 Приложения 3.
По указанному правилу производим отбор чисел и их цифр: 66 194, 28 926, 99547, 16 625, 45 515, 67 953, 78240, 43 195, 24 837, 32 511, 00833, 88000, 67299, 68 215, 11 274. Если генеральное множество содержит, например, 70 единиц, то номера 99547, 78240, 00833 не используются. Если выборка бесповторная, то раз отобранная единица, например, с номером 67 (67953), в дальнейшем отборе не участвует.
Вместо ТСЧ можно использовать генераторы случайных чисел. В качестве генератора можно использовать Microsoft Office Excel. Для генераци случайных чисел с помощью Excel можно использовать функции СЛУЧМЕЖДУ, СЛЧИС или воспользоваться командой Данные à Анализ данных à Генерация случайных чисел. Если кнопка Анализ данных отсутствует на вкладке Данные, то нужно подключить Пакет анализа: Файл à Параметры à Надстройки à Перейти à Пакет анализа.
Из таблицы исходных данных выписываем значения изучаемого признака 
у единиц, отобранных в выборку. Например, при изучении среднедушевых расходов населения РФ отобраны 10 территорий с указанными номерами и по ним собраны сведения о сумме ежемесячных среднедушевых расходов населения, тыс. руб.
| N | 
| 
| 
|  ,%
| ||||||||||
| п/п | ||||||||||||||
| X | 12,82 | 1,4 | 1,59 | 1,48 | 1,22 | 1,14 | 1,59 | 2,26 | 2,65 | 1,83 | 27,98 | 2,798 | 3,37 | |
| n’ | — | + | + | + | + | + | + | — | — | + | х | х | х |
Рассчитаем =2,798 тыс.руб., 
=3,37 тыс.руб., число территорий n’ =7, где расходы меньше среднедушевых ежемесячных ресурсов семьи, которые составляют 2,17 тыс. руб., и их долю 
=0,70.
Определим значения средних возможных ошибок средней и доли:
(тыс.руб.);
или 13,5%.
С вероятностью p=0,972 определим величину предельных ошибок средней и доли. Для p=0,972 коэффициент доверия t=2,2 (см. табл. 1, Приложение 3).
Тогда 
(тыс.руб.); 
или 29,7%.
Определим границы доверительного интервала возможных значений генеральной средней 
и генеральной доли 
.
Границы значений генеральной средней: 
С вероятностью 97,2% можно утверждать, что уровень среднемесячных душевых расходов населения РФ находится в интервале от 0,609 до 4,987 тыс. руб. Возможные значения генеральной средней располагаются в достаточно широких границах, это указывает на невысокую точность выводов. Но при этом высока надёжность границ, так как они позволяют оценить значение генеральной средней по результатам 97,2% всех возможных выборок данного объёма.
Значение генеральной доли будет находится в интервале: 
. С вероятностью 97,2% можно утверждать, что доля территорий, где расходы меньше средних ресурсов семьи будет находиться в интервале от 40,3% до 99,7%. Границы доверительного интервала также достаточно широкие, но они сочетаются с высокой вероятностью отражения значения генеральной доли. Основная причина широких границ доверительного интервала в том, что значения величины расходов X характеризуются чрезвычайно высокой вариацией (
), которая объясняется присутствием в выборке территории с порядковым номером 11 (г.Москва; X11 = 12,82 тыс.руб.), для которой характерно аномально высокое значение изучаемого признака. В том случае, если бы состав объектов выборки сформировался иначе и указанная территория в выборку не попала, результаты были бы точнее.
Задача 9.
Решение задачи №9 предполагает изучение корреляционной связи двух переменных методом наименьших квадратов (МНК). Покажем порядок решения на примере данных за 2000 год по территориям Северо-Западного федерального округа
Предварительное представление об изучаемой связи даёт исходное множество территорий, ранжированное по значению фактора X, а также график зависимости результата Y от фактора X. Для построения графика расположим территории по возрастанию значений фактора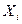 
. По графику сделаем вывод о наличии линейной связи результата Y с фактором X. См. табл. 1.
Таблица 1.
| Территории Северо-Западного федерального округа[1] | Общая сумма доходов населения за год, млрд. руб. | Оборот розничной торговли за год, млрд. руб. |
| 
| |
| 1. Псковская обл. | 11,6 | 7,3 |
| 2. Новгородская обл. | 14,8 | 9,3 |
| 3. Калининградская обл. | 19,0 | 14,0 |
| 4. Респ. Карелия | 19,1 | 9,4 |
| 5. Ленинградская обл. | 26,2 | 15,6 |
| 6. Вологодская обл. | 27,5 | 12,1 |
| 7. Архангельская обл. | 30,0 | 16,3 |
| 8. Респ. Коми | 37,3 | 16,7 |
| 9. Мурманская обл. | 39,5 | 20,5 |
| Итого | 225,0 | 121,2 |
| Средняя | 25,0 | 13,47 |
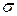
| 9,120 | 4,036 |
| Дисперсия, D | 83,182 | 16,289 |
Для отображения линейной формы связи переменных построим уравнения прямой: 
. Расчёт неизвестных параметров 
и 
выполняется методом наименьших квадратов (МНК), решая систему нормальных уравнений с использованием определителей второго порядка Δ, Δа0 и Δа1. Расчётные процедуры оформляются в разработочной таблице. См. табл.2.
Таблица 2.
| № | 
| 
| 
| 
| 
| 
| 
|
| А | |||||||
| 11,6 | 7,3 | 134,6 | 84,7 | 8,1 | -0,8 | 5,9 | |
| 14,8 | 9,3 | 219,0 | 137,6 | 9,4 | -0,1 | 0,7 | |
| 19,0 | 14,0 | 361,0 | 266,0 | 11,1 | 2,9 | 21,5 | |
| 19,1 | 9,4 | 364,8 | 179,5 | 11,1 | -1,7 | 12,6 | |
| 26,2 | 15,6 | 686,4 | 408,7 | 13,9 | 1,7 | 12,6 | |
| 27,5 | 12,1 | 756,3 | 332,8 | 14,5 | -2,4 | 17,8 | |
| 30,0 | 16,3 | 900,0 | 489,0 | 15,5 | 0,8 | 5,9 | |
| 37,3 | 16,7 | 1391,3 | 622,9 | 18,4 | -1,7 | 12,6 | |
| 39,5 | 20,5 | 1560,3 | 809,8 | 19,3 | 1,2 | 8,9 | |
| Итого | 225,0 | 121,2 | 6373,6 | 3331,0 | 121,2 | 0,0 | 98,5 |
| Средняя | 25,0 | 13,5 | — | — | — | — | 10,9 |
| Сигма | 9,12 | 4,04 | — | — | — | — | — |
| Дисперсия, D | 83,18 | 16,29 | — | — | — | — | — |
| Δ= | 6737,76 | — | — | — | — | — | — |
| Δа0= | 23012,4 | 
| 3,415 | — | — | — | — |
| Δа1= | 2708,91 | 
| 0,402 | — | — | — | — |
Расчёт определителей выполняется по следующим формулам:
Определитель системы 
9⋅6373,6 – 225,0⋅225,0 = 6737,76;
Определитель свободного члена уравнения 
= 121,2⋅6373,6 – 3331,0⋅225,0 = 23012,4.
Определитель коэффициента регрессии: 
= 9⋅3331,0 – 121,2⋅225,0 = 2708,91.
Параметры уравнения регрессии имеют следующие значения:
; 
.
Для расчетов определителей можно использовать функцию Microsoft Office Excel МОПРЕД. Кроме того, определить значения параметров уравнения регрессии можно также с помощью функций ОТРЕЗОК и НАКЛОН. Так же оба значения можно найти, использовав функцию ЛИНЕЙН.
Теоретическое уравнение регрессии следующего вида: 
Коэффициент регрессии а1 = 0,402 означает, что при увеличении доходов населения на 1 тыс. руб. (от своей средней) объём розничного товарооборота возрастёт на 0,402 млрд. руб. (от своей средней).
Свободный член уравнения а0 = 3,415 оценивает влияние прочих факторов, оказывающих воздействие на объём розничного товарооборота.
Относительную оценку силы связи даёт общий (средний) коэффициент эластичности: 
. В нашем случае, когда рассматривается линейная зависимость, расчётная формула преобразуется к виду: 
Это означает, что при изменении общей суммы доходов населения на 1% от своей средней оборот розничной торговли увеличивается на 0,744 процента от своей средней.
Оценку тесноты связи дают линейный коэффициент парной корреляции и детерминации:
; 
Коэффициент корреляции, величина которого больше 0 и составляет 0,9075, показывает, что выявлена прямо пропорциональная, весьма тесная зависимость между общей суммой доходов населения за год и оборотом розничной торговли за год. Коэффициент детерминации, равный 0,824, устанавливает, что вариация оборота розничной торговли на 82,4% (из 100%) предопределена вариацией общей суммы доходов населения; роль прочих факторов, влияющих на розничный товарооборот, определяется в 17,6%, что является сравнительно небольшой величиной.
Для определения расчётных значений результата 
подставим в полученное уравнение фактические значения фактора X. Например,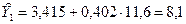 
. См. гр. 5 расчётной таблицы. По парам значений . и Xфакт. строим теоретическую линию регрессии.
Оценку качества модели даёт скорректированная средняя ошибки аппроксимации:
.
В нашем случае, скорректированная ошибка аппроксимации составляет 10,2%. Она указывает на невысокое качество построенной линейной модели и ограничивает её использование для выполнения точных прогнозных расчётов.
Задача 10.
Решение задачи № 10 начинаем с определения вида динамического ряда: является он интервальным или моментным. Формальной отличительной чертой моментного ряда является заданность его значений по состоянию на определённую дату. Значения уровней интервального динамического ряда формируются в течение определённого периода времени и поэтому приводятся за определённый отрезок, интервал времени.
Перечень показателей динамики за каждый год периода включает в себя: а) абсолютный прирост – d (цепной и базисный); б) абсолютное ускорение – D; в) темп роста (цепной и базисный) – К; г) относительное ускорение – U; д) темп прироста (цепной и базисный) – T; е) абсолютное значение 1% прироста – А. Результаты оформляются в расчётной таблице.
Абсолютное ускорение Dt показывает на какую величину изменился абсолютный прирост за данный год по сравнению с абсолютным приростом за предыдущий год: 
. Относительное ускорение Ut показывает во сколько раз темп роста данного года отличается от темпа роста предыдущего года: 
.
Абсолютное значение 1% прироста рассчитывается по следующей схеме:
.
С помощью показателей динамики за каждый год и графика проводится периодизация динамического ряда, то есть изучаемый отрезок времени разделяется на качественно однородные периоды, для каждого из которых характерна специфическая форма основной тенденции. Особенности каждого периода находят своё количественное отражение в значениях динамических средних. Перечень динамических средних включает: а) среднегодовой уровень ряда – 
; б) среднегодовой абсолютный прирост – 
; в) среднегодовой темп роста –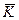 
. Порядок их расчёта рассмотрим на примере.
Количество рублёвых счетов вкладчиков в учреждениях Сберегательного банка РФ, на начало года,млн. счетов - Qt.
| Годы | |||||||
| Qt., млн. счетов. | 234,1 | 226,0 | 225,1 | 226,0 | 230,1 | 232,9 | 237,3 |
| Периоды | I-й период, содержит 4 года | II-й период, содержит 3 года |
В данном примере представлены значения уровней моментного ряда на начало года. Рассматриваемый 7-летний отрезок времени содержит два периода: I-ый период: 2000 – 2003 гг., то есть с 1.01.2000 по 1.01. 2004 г.; II-ой период: 2004 – 2006 гг., то есть с 1.01.2004 по 1.01.2007 г.
Среднегодовой уровень интервального и моментного ряда рассчитывается по-разному. По интервальному ряду используется: а) простая арифметическая, если расчёт проводится по значениям первичного признака – 
; б) взвешенная арифметическая или гармоническая в тех случаях, когда расчёт проводится по значениям вторичного признака:
или 
Среднегодовой уровень моментного ряда обычно рассчитывается по формуле средней хронологической: 
.
Приведём порядок расчёта динамических средних по каждому периоду по материалам заданного динамического ряда, обращая особое внимание на дату регистрации уровней ряда – начало года.
(млн. счетов)
(млн. счетов).
Во втором периоде по сравнению с первым периодом среднегодовое число счетов было больше на 2,2% (
).
Расчёт показателя среднегодового абсолютного прироста по интервальным и по моментным рядам выполняется одинаково. Но для разных периодов могут быть использованы разные расчётные формулы: 
; 
; где 
– уровень последнего года данного периода; 
– уровень последнего года предыдущего периода; 
– уровень первого года данного периода; 
– число лет в конкретном периоде. При расчётах по моментным рядам особое внимание обращаем на дату регистрации уровня ряда: на начало года или на конец года, и на то, какой период времени она характеризует
В нашем примере: 
(млн. счетов);
(млн. счетов)
В первом периоде число счетов ежегодно сокращалось в среднем на 2,3 млн., а во втором периоде число счетов ежегодно увеличивалось в среднем на 4,1 млн.
Расчёт показателей среднегодового темпа роста по моментным и интервальным рядам выполняется одинаково. Но для разных периодов используются разные расчётные формулы:
; 
.