Лекция 2
Теоремы умножения и сложения вероятностей
Если опыт включает в себя несколько событий, то применяют теоремы усножения или сложения вероятностей.
Теоремы умножения вероятностей.
Перемножать вероятности нужно при решении задач на поиск вероятности взаимосвязанных событий. Причем эти события могут зависить или не зависеть друг от друга. Напомню, что событие A является зависимым от события B, если оно не происходит до тех пор, пока не произойдет событие B. Например, пока гром не грянет (B), мужик не перекреститься (A).
Вероятность появления события А при условии, что первое событие В имело место, называется условной вероятностью и обозначается 
.
В теории множеств произведение событий это их пересечение. Произведением событий 
и 
называется событие 
, состоящее в появлении события и события вместе, одновременно.
Теорема умножения вероятностей зависимых событий записывается так:
.
Пример 1. В вагоне скорого поезда Днепропетровск-Киев всего пятьдесят четыре места, из которых 16 неудачных (лицом к лицу). Вы в кассе берете билеты и не зная какие номера неудачные называете два номера. Найти вероятность того, что оба места окажутся плохими.
Решение: Вероятность купить первый неудачный билет вычисляется по формуле классической вероятности: 
. Вероятность купить второй неудачный билет является условной вероятностью и определяется как: 
. По теореме умножения вероятностей:
.
Для множества зависимых событий 
верно равенство:
,
если все участвующие в нём условные вероятности определены.
Пример 2. В урне, содержащей 10 шаров, находится 6 белых и 4 черных шаров. Извлекаются последовательно 3 шара. Найти вероятность того, что все извлеченные шары белые, если шары в урну не возвращаются.
|
|
Решение: С каждым извлечением изменяется состав шаров в урне, и тогда: 
.
; 
; 
.
.
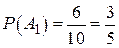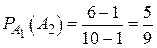Напомню, что если появление события не изменяет вероятность появления события , то эти события называются независимыми. Если события независимы, то теорема умножения вероятностей независимых событий записывается следующим образом: 
.
Пример 3. В урне, содержащей 10 шаров, находится 6 белых и 4 черных шаров. Извлекаются последовательно 3 шара. Найти вероятность того, что все извлеченные шары белые, если шары после извлечения возвращаются в урну.
Решение. Вероятность извлечения первого белого шара (событие 
) равна 
. Если шар возвращается в урну, то при последующем извлечении эта вероятность не изменяется 
(события 
и 
независимые). Вероятность извлечения белого шара в каждом из 3 извлечений с возвращением равна: 
.
Теорема сложения вероятностей.
Суммой событий 
называется событие, состоящее в появлении события или события или обоих вместе (если они совместимы). В теории множеств это объединение событий.
Напомню, что события и называются совместимыми, если появление одного из них не исключает появление другого. В противном случае они называются несовместимыми.
Для двух несовместных событий: 
.
Вероятность суммы двух совместных событий равна:
.
Для трех совместных событий вероятность суммы событий равна:
Пример 4. Найти вероятность того, что при броске игральной кости выпало четное число очков.
Решение. Обозначим события: 
, 
, 
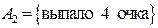. Эти события несовместны, поэтому:
|
|
.
Если задача состоит в поиске вероятности хотя бы одного события , то она проще решается через противоположное событие (не появилось ни одного события):
.
Следствие 
Пример 5. Монета брошена два раза. Найти вероятность того, что хотя бы один раз появится «герб».
Решение. Поскольку было два бросания, то вероятность того, что герб не появиться ни разу равна: 
.
Затем, находим 
.
Пример 6. Два игрока поочередно бросают правильную шестигранную игральную кость, но не более двух раз каждый. Игра заканчивается при первом появлении 6 очков. Найти вероятность победы первого и второго игрока, а также вероятность того, что ни у одного игрока не выпало 6 очков.
Решение. Обозначим события: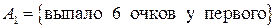 
, 
то же у второго, тогда 
противоположные события (не выпало 6 очков соответственно ни у первого ни у второго игроков), причём:
Возможные исходы в четырех партиях:
.
В первом и третьем случае побеждает первый игрок, эти события несовместимые, следовательно, вероятность победы первого игрока в четырех партиях (в первой или в третьей) есть сумма вероятностей:
.
Для второго игрока:
Ни у одного игрока не выпало 6 очков:
